2015-06-26
200Рассмотрим ситуацию: малая открытая экономика состоит из N идентичных фирм, в ней существует постоянное число работоспособных людей L̅, а уровень цен P формируется экзогенно. Обязательно присутствует некоторое число безработных, что даёт фирмам полную свободу в выборе з./п. (фирмы идентичны, поэтому w* и L для каждой из них одни и те же). Общее число занятых составляет N*L, незанятых L̅-NL, а уровень безработицы равен:
u= (L̅-NL)/ L̅ (6)
Подставив этот показатель в условия максимизации прибыли, можно вычислить оптимальную заработную плату и число работников, т.е. w* и L*. Предположим, что каждая фирма установила оптимальную з./п. и заключила контракты с L работников, сделав з./п. жесткой, т.е. w* = w̅*. В соответствии с этим, усилия работников принимают вид:
e = e(u;w*/P) (7)
Сразу после заключения контрактов произошёл абсолютно неожиданный негативный экономический шок (например, снижение цен на продукцию фирм, т.е. P↓).
Описываемая модель объясняет, какое влияние на уровень вынужденной безработицы окажет сложившаяся ситуация.
|
|
|
В неожиданно изменившейся макросреде существующая з./п. не является оптимальной с точки зрения максимизации прибыли фирм, но её изменение из-за условия жёсткости невозможно, и единственным способом воздействия становится изменение числа работников.
Единственное новое условие максимизации прибыли принимает вид:
PF′(e∙L)∙e –w* = 0 (8)
В теории жёсткой заработной платы предполагается, что усилия работников никак не изменяются в ответ на раздражители, то есть e – const. В этой ситуации взаимосвязь уровня занятости и изменений макросреды определяется с помощью равенства, получаемого в результате полного дифференцирования выражения (8) по L и P:
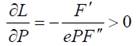(9)
Если же учитываются элементы теории эффективной заработной платы, старание работников не является постоянным, и прямое вычисление корреляции уровня занятости и цен путем подстановки равенств (6) и (7) в (8) и полного дифференцирования по L и P не даст возможности заметить все экономические зависимости, поэтому для расчёта примем L как функцию от P и e: L=f(e;P):
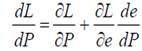
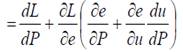
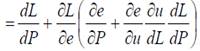(10)
Напомним, что é u= e1 и é (w/P) = e2. Из равенств (6) и (7) следует:
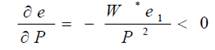(11)
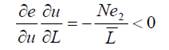(12)
Таким образом, величина и знак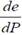 
зависят исключительно от знака выражения 
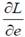, характеризующего зависимость между старанием рабочих и уровнем занятости в экономике. Чтобы, в свою очередь, оценить 
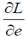, необходимо найти и преобразовать полную производную условия (8) по L и e:
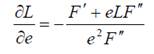(13)
Поскольку F́ ́ (L)<0, ключевое отношение имеет тот же знак, что у выражения F́ + e∙L∙F́ ́. Таким образом, если F́ + e∙L∙F́ ́ >0, то и 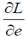>0, и наоборот.
|
|
|
Прикладываемые работниками усилия эндогенны, поэтому вызванные шоком сокращения (u↑) и дефляция (w/P↑), при неизменности всех остальных факторов, приведут к их росту и увеличению e и общей эффективности труда (e∙L). Образуется следующая дилемма: если занятые начнут работать интенсивнее может произойти увольнение фирмой части рабочих в соответствии с законом убывающей предельной полезности труда. С другой стороны, с увеличением усилий работника возрастает его ценность для компании. Направление, которое будет выбрано фирмами, зависит от строения конкретной производственной функции: если MPL снижается относительно медленно (|F́ ́ | невелик), то фирмы предпочтут сохранять работников или увеличивать их число; если же наоборот, компаниям выгоднее увольнять сотрудников.
Сопоставляя (9) и (10), можно сформулировать ответ на главный вопрос модели: изменение экзогенных факторов действительно влияет на уровень занятости в экономике, и силу этого влияния можно оценить с помощью различных теорий. Если использовать для анализа исключительно теорию жёсткой заработной платы, игнорируя учение об эффективной и полагая усилия работников постоянными, воздействие экономических шоков будет переоценено (если F́ + e∙L∙F́ ́ >0) или недооценено (если F́ + e∙L∙F́ ́ >0) по сравнению с данными, получаемыми при помощи объединённых моделей.
Для количественной оценки зависимости уровня занятости от неожиданно изменяющегося экзогенного параметра с помощью объединённых моделей необходимо преобразовать выражение (9):
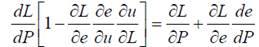(14)
Подставив в него (9),(11),(12),(13), получаем:
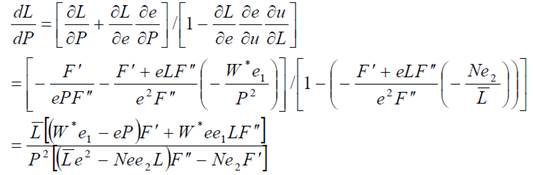(15)
В конце концов, объединив (13), (14), (15), получаем абсолютное значение воздействия шока на уровень занятости в описанной экономической системе:
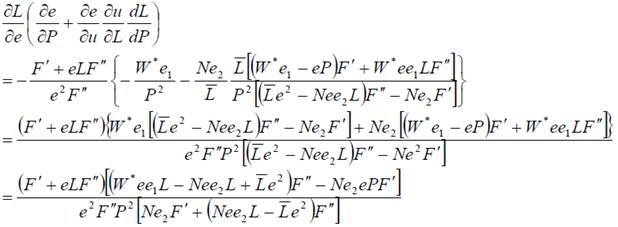
Итак, фирмы могут как увольнять, так и сохранять работников в ответ на изменения в прилагаемых ими усилиях под воздействием экономических шоков или рецессий. В связи с этим, оценки влияния резких изменений экзогенных параметров на уровень безработицы, произведённые с помощью модели жёсткой з./п. и её комбинации с моделью эффективной з./п. могут сильно отличаться друг от друга
