5. Вычисление значений элементарных функций от переменной 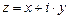 .
.
Образцы стандартных примеров по разделу Некоторые сведения из ТФКП:
· Изобразить на плоскости и записать в показательной форме: 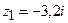 ,
, 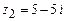 ,
, 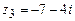 ,
, 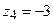 ,
, 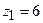 .
.
· Вычислить: 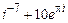 ;
; 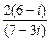 ;
; 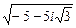 ;
; 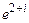 .
.
· Вычислить: 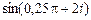 ,
, 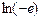 .
.
Вопросы к разделу «Ряды»
1. Частичная сумма для числового ряда 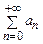 . Определение
. Определение 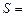
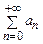 . Сходящиеся и расходящиеся ряды.
. Сходящиеся и расходящиеся ряды.
2. Необходимый признак сходимости числового ряда 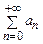 .
.
3. Интегральный признак Коши сходимости числового ряда 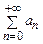 с положительными слагаемыми (
с положительными слагаемыми (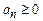 для
для 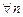 ).
).
4. Гармонический ряд. Обобщённый гармонический ряд. Сходимость гармонического и обобщённого гармонического рядов 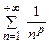 .
.
5. Признаки сравнения сходимости знакоположительных рядов.
6. Знакопеременные числовые ряды. Абсолютная и условная сходимость.
7. Признак Даламбера (д’Аламбера) абсолютной сходимости ряда.
8. Знакочередующиеся ряды. Признак Лейбница сходимости знакочередующихся рядов.
9. Оценка погрешности при замене 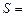
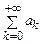 частичной суммой
частичной суммой 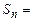
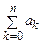 (на примерах).
(на примерах).
10. Функциональные ряды 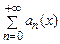 . Область сходимости функционального ряда.
. Область сходимости функционального ряда.
11. Степенные ряды 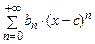 . Структура области сходимости степенного ряда. Радиус сходимости степенного ряда.
. Структура области сходимости степенного ряда. Радиус сходимости степенного ряда.
12. Ряды Тейлора и Маклорена для функции 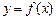 . Достаточное условие выполнения равенства
. Достаточное условие выполнения равенства 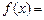
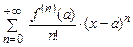 .
.
13. Ряды Маклорена для функций 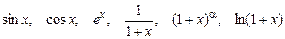 .
.
14. Использование рядов в приближённых вычислениях (с оценкой погрешности, на примерах).
Образцы стандартных примеров по разделу Ряды:
· Дан ряд 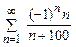 (или
(или 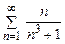 , или
, или 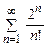 и т.п.) Найти сумму первых четырёх слагаемых. Исследовать сходимость ряда.
и т.п.) Найти сумму первых четырёх слагаемых. Исследовать сходимость ряда.
· Найти область сходимости степенного ряда 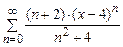 .
.
· Разложить функцию 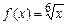 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 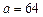 (или функцию
(или функцию 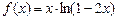 в окрестности точки
в окрестности точки 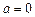 и т.п.). Указать область сходимости ряда.
и т.п.). Указать область сходимости ряда.
· Вычислить приближённо 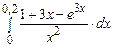 (или
(или 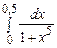 и т.п.) (с погрешностью не более 1%), используя разложение подынтегральной функции в ряд.
и т.п.) (с погрешностью не более 1%), используя разложение подынтегральной функции в ряд.
Вопросы к разделу «Дифференциальные уравнения»
1. ДУ (дифференциальное уравнение) первого порядка, общий вид. ДУ первого порядка, разрешённое относительно производной. Общее, частное и особое решения ДУ первого порядка.
2. ДУ с разделяющимися переменными.
3. Линейное ДУ первого порядка.
4. Задача Коши для ДУ первого порядка. Теорема существования и единственности решения задачи Коши.
5. ДУ 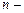 ого порядка, общий вид. ДУ
ого порядка, общий вид. ДУ 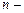 ого порядка, разрешённое относительно старшей производной. Общее решение, частное решение.
ого порядка, разрешённое относительно старшей производной. Общее решение, частное решение.
6. Задача Коши для ДУ 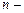 ого порядка. Теорема существования и единственности решения задачи Коши.
ого порядка. Теорема существования и единственности решения задачи Коши.
7. Линейно зависимые и линейно независимые функции на 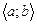 . Определитель Вронского.
. Определитель Вронского.
8. Линейное ДУ 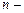 ого порядка, однородное и неоднородное. Расшифровка символа
ого порядка, однородное и неоднородное. Расшифровка символа 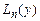 .
.
9. Теорема о структуре общего решения уравнения 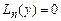 . Фундаментальная система решений.
. Фундаментальная система решений.
10. Теорема о структуре общего решения уравнения 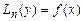 .
.
11. Линейные ДУ 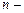 ого порядка с постоянными коэффициентами, однородные. Характеристическое уравнение. Вид фундаментальной системы решений в зависимости от значений корней характеристического уравнения.
ого порядка с постоянными коэффициентами, однородные. Характеристическое уравнение. Вид фундаментальной системы решений в зависимости от значений корней характеристического уравнения.
12. Линейные ДУ 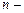 ого порядка с постоянными коэффициентами, неоднородные. Метод неопределённых коэффициентов для решения уравнений с правой частью вида
ого порядка с постоянными коэффициентами, неоднородные. Метод неопределённых коэффициентов для решения уравнений с правой частью вида 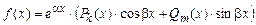 (на примерах).
(на примерах).
13. Преобразование выражений 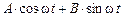 ) к виду
) к виду 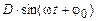 .
.
Образцы стандартных примеров по разделу Дифференциальные уравнения:
· Найти общее решение уравнения 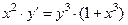 .
.
· Найти решение задачи Коши 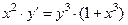 ,
, 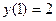 .
.
· Найти общее решение дифференциального уравнения 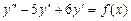 при
при 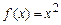 , или
, или 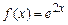 , или
, или 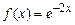 , или
, или 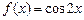 и т.п.
и т.п.
· Найти частное решение дифференциального уравнения 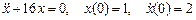 . Ответ представить в виде
. Ответ представить в виде 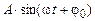 .
.
· Найти частное решение дифференциального уравнения 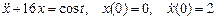 .
.
 2015-06-24
2015-06-24 576
576






