Это булева матрица графа порядка n2.
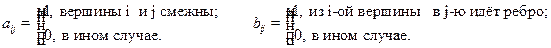
Просматривая строки и столбцы матриц смежности, находим соответствующие множества смежности; сумма единиц равна степени вершины. Для орграфов соответственно множество потомков и множество предшественников (родителей). — В каждой строке матрицы смежности орграфа количество единиц равно d+, а в каждом столбце количество единиц равно d–.
Сложность – O(n2).
Ранг матрицы смежности называется рангом графа. Обозначение: rank G. Характеристические числа графа – характеристические числа его матрицы смежности.
Для изоморфных графов матрицы смежности отличаются перестановками строк и столбцов – следовательно, характеристические многочлены изоморфных графов совпадают.
rank A=3, cA(l)=l(l+1)2(l–2); rank B=3, cB(l)=l(l–1)(l2+l+1).
Транзитивное замыкание графа:
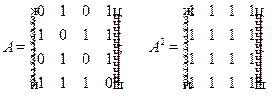
Орграфа:
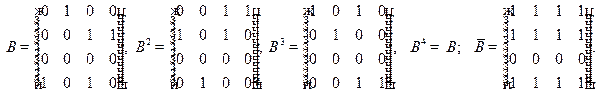
 2015-06-24
2015-06-24 1059
1059
