Схема Бернулли. Формула Бернулли. Предельные теоремы Муавра-Лапласа и Пуассона

Лабораторная работа 2

Вероятность того, что в n независимых испытаниях число успехов наступит ровно m раз (Схема Бернулли B(n;p)), выражается формулой Бернулли

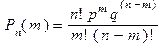
где p-вероятность появления успеха в каждом испытании; q=1-p- вероятность неудачи.(пример см.в конце работы)

Если n велико (не меньше 10) можно использовать теоремы Муавра-Лапласа и теорему Пуассона.

В случае, когда n велико, а p мало (обычно p<0,1; npq<10) (схема редких явлений) вместо формулы Бернулли применяют приближенную формулу Пуассона

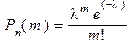, где .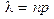

Теоремы Муавра-Лапласа применяются для приближенного вычисления вероятносте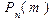й и 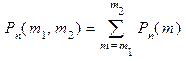в независимых испытаниях Бернулли при больших n, m, 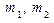, когда вероятность p наступления успеха в одном испытании постоянна, величины 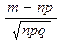, , 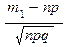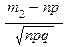равномерно ограничены по n, m, .

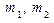Локальная формула. Вероятность того, что в n независимых испытаниях успех наступит ровно m раз, равна

,

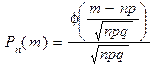где p - вероятность появления успеха в каждом испытании, q=1-p, .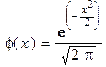

Интегральная формула. Вероятность того, что в n независимых испытаниях число успехов находится между 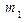и 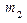, равна

,

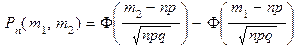где p- вероятность появления успеха в каждом испытании, q=1-p, 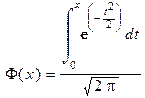- функция Лапласа.

Приближенные формулы Муавра-Лапласа применяют в случаях, когда p и q не малы, а .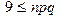

Задача 1. В схеме Бернулли B(10; 0,4) Найти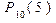

> n:=10;P(n,5):=binomial(n,5)*(.4)^5*(1-.4)^(n-5);

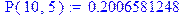
Задача 2. Вычислить вероятности того, что при 100-кратном бросании монеты герб выпадет а) ровно 50 раз; б) ровно 60 раз.

Решение. Условия применения локальной теоремы Муавра-Лапласа выполняются, поэтому воспользуемся ею:

а)

> n:=100;p:=0.5;q:=0.5;k:=50;

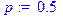
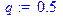
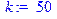
> x:=(k-n*p)/sqrt(n*p*q);

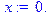
> f(x):=simplify(1/sqrt(2*Pi)*exp(-x^2/2));

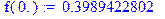
> pn(k):=1/sqrt(n*p*q)*f(x);

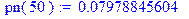
Пункт б) выполнить самостоятельно

Проанализируем изменение вероятности, в зависимости от числа появлений герба в этой схеме. Пусть к меняется от 40 до60 появлений. Построим график

> restart:n:=100;p:=0.5;q:=0.5;x:=(k-n*p)/sqrt(n*p*q);f(x):=(1/sqrt(2*Pi)*exp(-x^2/2));pn(k):=1/sqrt(n*p*q)*f(x);plot(pn(k),k=40..60);

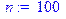
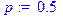
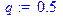
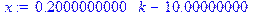
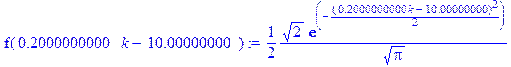
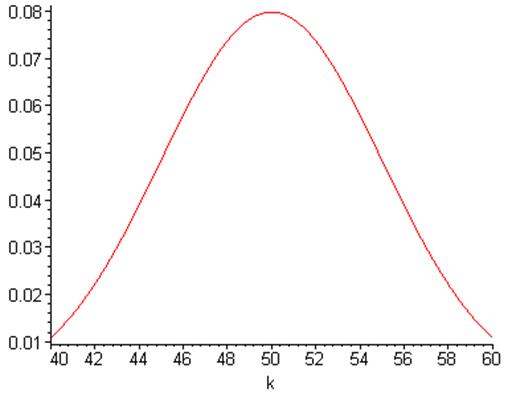
Очевидно, что наивероятнейшее число наступления успеха равняется 50.

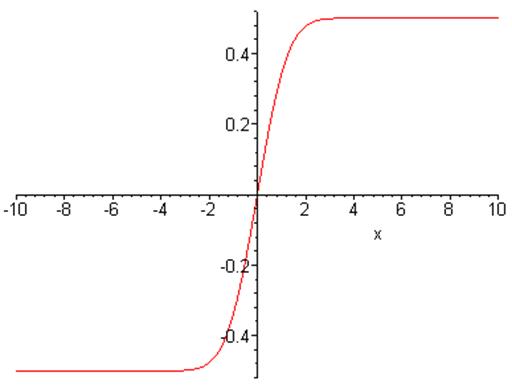
Задача 3. Построить график функции Лапласа.

Решение. Очистим x:

> x:='x':

Зададим функцию Лапласа

> Phi(x):=1/sqrt(2*Pi)*int(exp(-t^2/2),t=0..x);

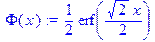
Построим график функции Лапласа

> plot(Phi(x),x);

Задача 4. Вычислить вероятность наступления случайного события от 790 до 830 раз в 900 независимых испытаниях, если p=0,9.

Решение. Выразим x1 и x2:

> x2:=(830-900*0.9)/sqrt(900*0.9*0.1);

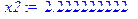
> x1:=(790-900*0.9)/sqrt(900*0.9*0.1);

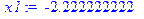
Вычислим искомую вероятность:

> P:=1/sqrt(2*Pi)*int(exp(-t^2/2),t=-infinity..x2)-1/sqrt(2*Pi)*int(exp(-t^2/2),t=-infinity..x1);

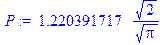
Оценим ее:

> evalf(P);

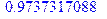
Решите задачи::

1) Какова вероятность того, что в столбике из 100 наугад отобранных монет число монет, расположенных "гербом" вверх, будет от 45 до 55?

2) Производство дает 1% брака. Какова вероятность того, что из взятых на исследование 900 изделий выбраковано будет а) ровно 9, б) не больше 9?

Решение а) Используем теорему Пуассона

> p:=.01;n:=900;lambda:=n*p;

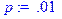
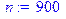
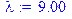
> P:=(lambda)^9/9!*exp(-lambda);

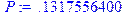
Пункт б) самостоятельно.

3) Игральную кость бросают 80 раз. Найти приближенно границы, в которых число выпадений шестерки будет заключено с вероятностью 0,9973.

4) Вероятность успеха в каждом испытании равна 0.25. Какова вероятность, что при 300 испытаниях успех наступит а) ровно 75 раз; б) ровно 85 раз?

5)Батарея дала 14 выстрелов по объекту, вероятность попадания в который равна 0,2. Найти наивероятнейшее число попаданий и вероятность этого числа попаданий.

6) Всхожесть семян данного сорта растений оценивается с вероятностью, равной 0,8. Какова вероятность того, что из пяти посеянных семян взойдут не менее четырех?

7) Вероятность рождения мальчика равна 0,515, девочки 0,485. В некоторой семье шестеро детей. Найти вероятность того, что среди них не более двух девочек.

8) Средняя плотность болезнетворных микробов в одном кубическом метре воздуха равна 100. Берется на пробу 2 кубических дециметра воздуха. Найти вероятность того, что в нем будет обнаружен хотя бы один микроб.

9) Сколько изюма должна в среднем содержать булочка, чтобы вероятность иметь хотя бы одну изюмину в булочке была не менее 0,99?

10) Рыбак забросил спиннинг 100 раз. Какова вероятность того, что он поймал хотя бы одну рыбу, если одна рыба приходится в среднем на 200 забрасываний?

11) Брошено 6 правильных игральных костей. Какова вероятность выпадения: а) хотя бы одной; б) ровно одной; в) ровно двух единиц? Найти точные значения и сравнить их со значениями, вычисленными по формуле Пуассона.

12) Монету бросают до тех пор, пока два раза подряд она не выпадет одной и той же стороной. Найти вероятности событий: а) опыт закончится не более чем за четыре бросания; б) опыт закончится за четное число бросаний.

13)В первые классы должно быть принято 200 детей. Определить вероятность того, что среди них окажется 100 девочек, если вероятность рождения мальчика равна 0.515.