Предположим, что испытание проведено и событие В при этом наступило. Проанализируем, как изменятся при этом вероятности гипотез.
По теореме умножения вероятностей имеем
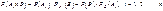
или 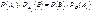 .
.
Отсюда получим
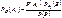 ,где
,где 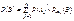
Полученная формула называется формулой Байеса, или формулой гипотез. Она позволяет переоценить вероятности гипотез после того, как событие В наступило в результате проведенного испытания, то есть найти новые условные вероятности гипотез PB(Ai), которые еще называют апостериорными.
Значение формулы Байеса состоит в том, что при наступлении события В, то есть по мере получения новой информации, можно проверять и корректировать выдвинутые до испытания гипотезы. Такой подход, называемый байесовским, дает возможность корректировать, например, управленческие решения в экономике.
1.8 Повторные независимые испытания. Вероятность наступления события при независимых испытаниях (формула Бернулли). Наивероятнейшая частота.
Пусть проводится n испытаний, в каждом из которых событие А может произойти или не произойти, причем вероятность события А от испытания к испытанию не меняется. Такие испытания называются независимыми. В противном случае испытания зависимы. Вероятность наступления события А при каждом испытании обозначим р, то есть P(A)=p, тогда 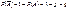 .
.
При n независимых испытаниях событие А практически может наступить любое число раз (m раз) в разных комбинациях с противоположным событием  (которое может наступить (n-m) раз).
(которое может наступить (n-m) раз).
Рассмотрим простейшую комбинацию:
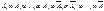 , то есть событие А наступает m раз подряд, а затем
, то есть событие А наступает m раз подряд, а затем 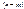 раз наступает событие
раз наступает событие  . Используя теорему умножения вероятностей независимых событий, получим
. Используя теорему умножения вероятностей независимых событий, получим 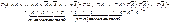
Различных комбинаций, в которых событие А наступает m раз, всего будет  , вероятность наступления каждой из этих комбинаций одинаковая и равна
, вероятность наступления каждой из этих комбинаций одинаковая и равна 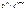 .
.
Вероятность наступления события А m раз при n испытаниях символически записывается так: 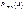 .
.
Итак, 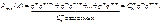
Таким образом, 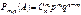 .
.
Полученная формула называется формулой Бернулли.
Наивероятнейшая частота
Частота m0 называется наивероятнейшая частота, если выполняются одновременно 2 условия
Рm0,n (A) ≥ Рm0 - 1,n (A)
Рm0,n (A) ≥ Рm0 + 1,n (A)
1)  *pm0*qn-m0≥
*pm0*qn-m0≥ 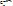 *pm0-1*qn-m0+1
*pm0-1*qn-m0+1
2)  *pm0*qn-m0≥
*pm0*qn-m0≥ 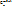 *pm0+1*qn-m0-1
*pm0+1*qn-m0-1
Разделим 1 на pm0-1qn-m0, a 2 на pm0 qn-m0-1
 p≥
p≥ 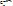 q
q
 ≥
≥ 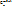 p
p
1) 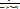 p≥
p≥ 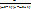 q
q
2) 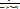 q≥
q≥ 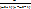 p
p
Домножаем 1 на 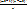 , 2 на
, 2 на 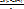
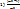 p≥
p≥ 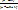 q
q
2) 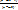 q≥
q≥ 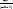 p
p
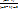 p≥
p≥ 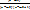 q
q
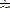 ≥
≥ 
1)  ≥
≥ 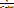 домножаем на m0
домножаем на m0
2) 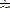 ≥
≥  домножаем на m0+1
домножаем на m0+1
1)p≥ 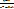 домножаем на (n-m0+1)
домножаем на (n-m0+1)
2) 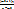 ≥ p домножаем на (n-m0)
≥ p домножаем на (n-m0)
1) (n-m0+1)p≥qm0
2) (m0+1)q≥(n-m0)p
1) np-m0p+p-qm0≥0
2) m0q+q-np+m0≥0
1) np+p-m0(p+q)≥0
2)q-np+m0(p+q)≥0
np+p≥m0
m0≥np-q
np-q≤ m0 ≤ np+p формула наивероятнейшей частоты
1.9 Теорема Пуассона
Пусть событие А - маловероятное, тогда вероятность его наступления при каждом испытании 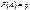 близка к нулю. В этом случае даже при большом числе испытаний
близка к нулю. В этом случае даже при большом числе испытаний 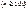 по небольшой величине произведения np
по небольшой величине произведения np 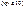 расчеты вероятностей
расчеты вероятностей  по формуле Муавра - Лапласа оказываются недостаточно точными. В таких случаях следует применять другую асимптотическую формулу - формулу Пуассона.
по формуле Муавра - Лапласа оказываются недостаточно точными. В таких случаях следует применять другую асимптотическую формулу - формулу Пуассона.
Теорема. Если вероятность р наступления события А при каждом испытании постоянна, но близка к нулю, число независимых испытаний n достаточно велико, а произведение np остается небольшим, то вероятность того, что событие А наступит m раз, приближенно равна
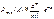 , где
, где 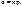
Доказательство. Действительно, пусть проводится n независимых испытаний, в результате которых событие А наступает с постоянной вероятностью р при каждом испытании. Вероятность наступления события А m раз при этих испытаниях найдем по формуле Бернулли
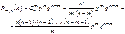
По условию теоремы a=np, отсюда p=a/n.
Тогда 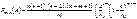 .
.
Запишем это равенство в таком виде 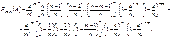
Так как по условию теоремы n достаточно велико, то множители 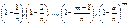 приближенно можно считать равными 1. Тогда, заменяя их в предыдущем равенстве единицей, получим приближенное значение
приближенно можно считать равными 1. Тогда, заменяя их в предыдущем равенстве единицей, получим приближенное значение 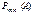 , а именно:
, а именно:
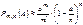 .
.
Известно, что 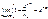 (следствие из второго замечательного предела). Тогда при достаточно больших n имеем
(следствие из второго замечательного предела). Тогда при достаточно больших n имеем 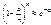 . Используя этот результат, получаем асимптотическую формулу расчета вероятности
. Используя этот результат, получаем асимптотическую формулу расчета вероятности 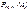 , называемую формулой Пуассона
, называемую формулой Пуассона
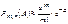 , где
, где 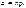
Вычисления Pm,n(A) по формуле Пуассона дают незначительную погрешность при выполнении следующего условия:a=np≤10. Для упрощения расчетов по рассматриваемой формуле составлена таблица ее значений (прил. 3).
1.10 Локальная теорема Муавра-Лапласа
Поэтому, когда число испытаний велико, для вычисления вероятности Pm,n(A) применять формулу Бернулли нецелесообразно. Нужны формулы, по которым достаточно точные значения вероятностей Pm,n (A) находились бы при сравнительно несложных вычислениях. Такими формулами являются формулы Муавра - Лапласа и Пуассона. Эти формулы являются асимптотическими.
Теорема. Если вероятность наступления события А в каждом из n испытаний постоянна и равна р, причем отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность Pm,n (A) того, что при n независимых испытаниях событие А наступит m раз, приближенно равна: 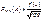 ,где функция
,где функция 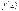 определяется равенством
определяется равенством 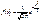 ,
, 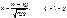 .
.
Теорему рассмотрим без доказательства, так как строгое доказательство ее выходит за рамки математического аппарата, который положен в основу настоящего пособия.
Итак, 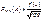 , где
, где 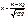 .
.
С возрастанием n относительная точность вычисления вероятностей 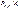 , получаемых по формуле Муавра - Лапласа, возрастает. Если выполняется условие
, получаемых по формуле Муавра - Лапласа, возрастает. Если выполняется условие 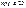 , то вычисления по рассматриваемой формуле дают приемлемую точность.
, то вычисления по рассматриваемой формуле дают приемлемую точность.
Для упрощения расчетов 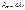 по формуле Муавра - Лапласа составлена таблица значений функции
по формуле Муавра - Лапласа составлена таблица значений функции 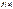 (прил. 1). Пользуясь данной таблицей, необходимо иметь в виду свойства этой функции, а именно:
(прил. 1). Пользуясь данной таблицей, необходимо иметь в виду свойства этой функции, а именно:
1) функция 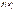 - четная, то есть
- четная, то есть 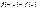 . Поэтому в таблице приведены значения функции только для положительных значений аргумента;
. Поэтому в таблице приведены значения функции только для положительных значений аргумента;
2) функция 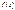 - монотонно убывающая при положительных значениях х. Уже при х=5
- монотонно убывающая при положительных значениях х. Уже при х=5 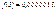 Следовательно, при
Следовательно, при 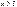 можно считать, что
можно считать, что 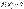 . Поэтому таблица значений функции
. Поэтому таблица значений функции 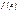 приводится только для
приводится только для 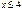 .
.
 2015-06-24
2015-06-24 638
638






