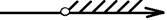· Для решения неравенства с одним неизвестным, которое сводится к линейному, нужно:
1. Если есть скобки, то раскрыть скобки.
2. Перенести члены, содержащие неизвестное, в левую часть, а члены, не содержащие неизвестное, в правую часть.
3. Привести подобные члены в обеих частях неравенства.
4. Разделить обе части неравенства на коэффициент при неизвестном, если он не равен нулю:
ü Если коэффициент число положительное, то знак неравенства не меняется.
ü Если коэффициент число отрицательное, то знак неравенства меняется на противоположный.
ОБРАЗЕЦ решения неравенства:
1) x – 5 £ -4
x £ -4 + 5
x £ 1
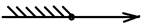 (- ¥; 1]
Ответ: (- ¥; 1]
(- ¥; 1]
Ответ: (- ¥; 1]
| 2)3х ³ -9
х ³ -9: 3
х ³ -3
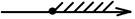 –3
[- 3; +¥)
Ответ: [- 3; +¥).
–3
[- 3; +¥)
Ответ: [- 3; +¥).
| ||||||
3)х + 1 > 7 – 2х
х + 2х > 7 – 1
3х > 6
х > 6: 3
 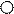
   х > 2 х > 2
2 (2; +¥) Ответ: (2; +¥). | 1 шаг перенесем член –2х из правой части неравенства в левую, изменив его знак на противоположный, а число 1 перенесем в правую часть со знаком «–». 2 шаг в обеих частях этого неравенства приведем подобные члены 3 шаг разделим обе части этого неравенства на 3; так как 3 положительное число, то знак неравенства не меняется | ||||||
4)3(х – 2) – 4(х + 1) < 2(х – 3) – 2
3х – 6 – 4х – 4 < 2х – 6 – 2
3х – 4х – 2х < - 6 – 2 + 6 + 4
–3х < 2
x < 2: (–3)
х > 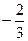
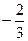 (-
(- 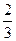 ; +¥)
Ответ: (- ; +¥)
Ответ: (- 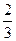 ; +¥). ; +¥).
| 1 шаг раскроем скобки 2 шаг перенесем члены, содержащие неизвестное, в левую часть, а члены, не содержащие неизвестное, в правую 3 шаг приведем подобные члены 4 шаг разделим обе части на -3; так как число -3 отрицательное, то знак неравенства меняем на противоположный | ||||||
5) 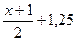 > > 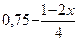
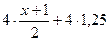 > > 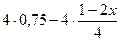 2(х + 1) + 5 > 3 – (1 – 2х)
2х + 2 + 5 > 3 – 1 + 2х
2х – 2х > 3 – 1 – 2 – 5
0х > -5
Ответ: х – любое число
2(х + 1) + 5 > 3 – (1 – 2х)
2х + 2 + 5 > 3 – 1 + 2х
2х – 2х > 3 – 1 – 2 – 5
0х > -5
Ответ: х – любое число
| 1) умножим обе части неравенства на 4(общий знаменатель) 2) раскроем скобки, используя правила раскрытия перенесем члены, содержащие неизвестное, в левую часть, а члены, не содержащие неизвестное, в правую часть 3) последнее неравенство является верным при любом значении х, т.к. его левая часть при любом х равна 0, а 0>-5. следовательно, любое значение х является решением данного неравенства | ||||||
| 6)5 – 3х < 3(2 – х) – 2 5 – 3х < 6 – 3х – 2 -3х + 3х < 6 – 2 – 5 0х < -1 Ответ: нет решений. | последнее неравенство не имеет решений, т.к. левая часть неравенства при любом значении х равна 0, а 0 < -1 неверно. Следовательно, исходное неравенство не имеет решений |
Решите по образцу неравенства:
1. 7, 2z > -27
2. -4,5x ³ 9
3. х + 2 ³ 10
4. -4 > 5 – у
5. 3z £ 2z + 4
6. -5 < 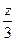 7.
7. 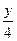 £ 7 £ 7
| 1. 2(3х – 7) – 5х £ 3х – 11 2. х – 4(х – 3) < 3 – 6х 3. 12х–16 ³ 11х +2(3х + 2) 4. 2х + 4(2х – 3) ³ 12х –11 5. 25 – х > 2 – 3(х – 6) | 1. 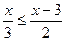 2.
2. 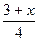 ³ ³ 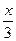 3.
3. 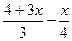 £ 1
4. £ 1
4. 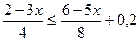 5.
5. 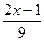 < < 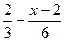
|
 2015-07-03
2015-07-03 435
435