1. Довести, що множина всіх цілих чисел, які діляться на 3, є абелевою групою відносно додавання.
2. Довести, що множина всіх векторів площини є абелевою групою відносно операції додавання.
3. У множині 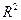 задано операцію
задано операцію 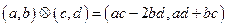 . Довести, що множина
. Довести, що множина 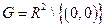 є групою відносно операції
є групою відносно операції 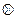 .
.
4. Задати таблицею Келі операцію 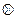 у множині
у множині 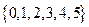 , якщо
, якщо 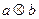 дорівнює остачі від ділення добутку
дорівнює остачі від ділення добутку 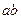 на число 6.
на число 6.
5. Довести, що множина всіх дійсних чисел виду 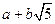 , де
, де 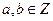 є комутативним кільцем з одиницею.
є комутативним кільцем з одиницею.
6. Чи є полем множина всіх чисел виду 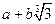 ;
; 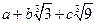 , де
, де 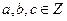 .
.
7. Нехай у множині 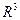 задано операції
задано операції
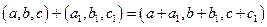
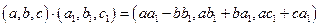 .
.
Чи є полем множина 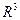 ?
?
8. Доведіть, що алгебраїчні структури є кільцем, але не полем.
1) Множина цілих чисел: операції множення та додавання.
2) Множина цілих чисел, кратних деякому числу 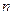 : операції множення та додавання.
: операції множення та додавання.
3) Множина дійсних чисел виду 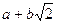 , де
, де 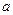 і
і 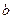 - цілі числа: операції множення та додавання.
- цілі числа: операції множення та додавання.
4) Множина многочленів з дійсними коефіцієнтами від заданої змінної 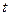 , в тому числі константи: операції множення та додавання.
, в тому числі константи: операції множення та додавання.
5) Множина один елемент 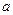 : операції визначено так
: операції визначено так 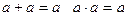 .
.
6) Множина пар 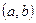 цілих чисел: операції визначено так
цілих чисел: операції визначено так 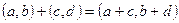 ,
, 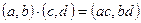 .
.
9. Доведіть, що алгебраїчні структури є полем.
1) Множина раціональних чисел: операції множення та додавання.
2) Множина дійсних чисел: операції множення та додавання.
3) Множина комплексних чисел: операції множення та додавання.
4) Множина дійсних чисел виду 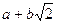 , де
, де 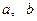 - раціональні числа: операції множення та додавання.
- раціональні числа: операції множення та додавання.
5) Множина двох елементів 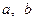 : операції визначено так
: операції визначено так  ,
, 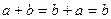 ,
, 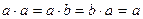 ,
, 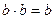 .
.
10. Визначте, чи замкнені дані операції відносно даних множин.
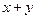
| 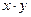
| 
| 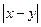
| 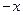
| 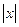
| |
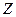
| ||||||
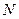
| ||||||
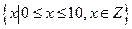
| ||||||
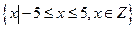
| ||||||
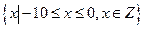
| ||||||
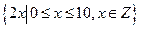
|
11. Побудуйте таблицю Келі для групи 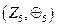 . Для кожного елемента визначте обернений.
. Для кожного елемента визначте обернений.
12. Доведуть двосторонню дистрибутивність множення 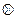 відносно віднімання
відносно віднімання 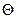 у кільці
у кільці 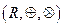 :
:
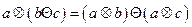 ;
; 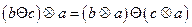 .
.
 2015-07-21
2015-07-21 484
484






