Азн.13.1. Вектары 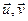 эўклідавай прасторы ε называюцца артаганальнымі, калі (
эўклідавай прасторы ε называюцца артаганальнымі, калі (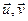 )=0.
)=0.
Ул-ць13.2. У эўклідавай прасторы ε:
1. Нулявы вектар і толькі ён артаганальны сам сябе;
2. Нулявы вектар і толькі ён артаганальны усім вектарам;
3. Калі вектар 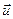 артаганальны вектарам
артаганальны вектарам 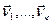 , тады ен артаганальны адвольнай іх лінейнай камбінацыі.
, тады ен артаганальны адвольнай іх лінейнай камбінацыі.
Доказ:
1. Калі 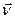 =
= 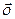 , тады па 12.7.1 (
, тады па 12.7.1 (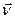 ,
, 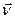 )=(
)=(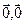 )=0; а калі
)=0; а калі 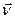 ≠
≠ 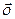 , тады па 12.7.4 (
, тады па 12.7.4 (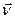 ,
, 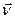 )>0.
)>0.
2. Калі 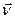 =0, тады
=0, тады 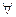
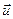 па 12.7.1 (
па 12.7.1 (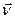 ,
, 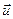 )=(
)=(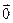 ,
, 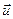 )=0; а калі
)=0; а калі 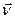 ≠
≠ 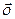 , тады па 12.1.4 (
, тады па 12.1.4 (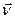 ,
, 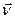 )>0.
)>0.
3. Калі 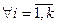
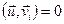 , тады
, тады 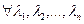 Î R па 12.3 маем
Î R па 12.3 маем 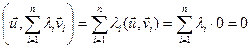 .
.
Ул-ць 13.3. Ненулявыя вектары 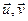 артаганальныя тады і толькі тады, калі вугал паміж імі роўны
артаганальныя тады і толькі тады, калі вугал паміж імі роўны 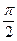 .
.
Ул-ць 13.4. Калі 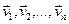 папарна артаганальныя ненулявыя вектары эўклідавай прасторы, тады яны лінейна незалежныя.
папарна артаганальныя ненулявыя вектары эўклідавай прасторы, тады яны лінейна незалежныя.
Доказ:
Няхай 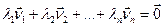 , тады:
, тады: 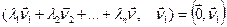 ;
;
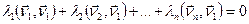 ;
; 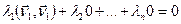 ;
; 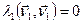 .
.
Па ўмове 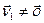 , значыцца, па 12.1 (
, значыцца, па 12.1 (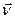 ,
, 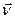 )>0, з чаго вынікае, што
)>0, з чаго вынікае, што 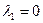 . Аналагічна даказваецца, што
. Аналагічна даказваецца, што 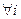
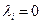 , што и трэба было даказаць.■
, што и трэба было даказаць.■
Ул-ць13.5. (Тэарэма Піфагора ў эўклідавай прасторы)
Калі 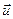 ,
, 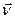 артаганальныя вектары эўклідавай прасторы, тады
артаганальныя вектары эўклідавай прасторы, тады 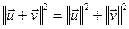 .
.
Доказ: 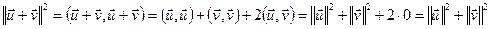 . ■
. ■
Ул-ць 13.6. (Уласцівасць паралелаграма ў эўклідавай прасторы)
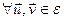
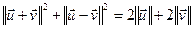
Доказ:
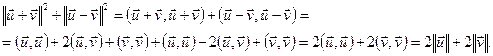 ■
■
 2015-07-14
2015-07-14 237
237






