Азн.15.1. Няхай ε – эўклідава прастора. Лінейнае пераўтварэнне f: ε 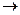 ε называецца артаганальным, калі
ε называецца артаганальным, калі 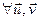 Î ε
Î ε 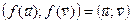 .
.
Прыклад. У эўклідавай прасторы V2 са скалярным здабыткам 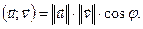
аператар f: V2 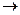 V2 ( паварот на вугал a з прыкладу 11.3) з’яўляецца артаганальным.
V2 ( паварот на вугал a з прыкладу 11.3) з’яўляецца артаганальным.
Ул-ць.15.2. Адвольнае артаганальнае пераўтварэнне прасторы ε n з’яўляецца аўтамарфізмам (гэта значыць, біектыўным пераўтварэннем ε n).
Доказ. Няхай f: ε n 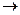 ε n – артаганальнае адлюстраванне. Дакажам ін’ектыўнасць f. Ад процілеглага.. Калі
ε n – артаганальнае адлюстраванне. Дакажам ін’ектыўнасць f. Ад процілеглага.. Калі 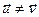 і
і 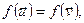 тады
тады 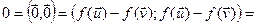
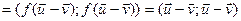 , значыцца,
, значыцца, 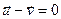 , а гэта супярэчыць умове
, а гэта супярэчыць умове 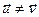 .
.
Дакажам сюр’ектыўнасць 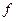 . Няхай f не з’яўляецца сюр’ектыўным, тады падпрастора
. Няхай f не з’яўляецца сюр’ектыўным, тады падпрастора 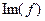 у ε n не роўная ε n. Калі
у ε n не роўная ε n. Калі 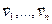 - базіс ў ε n, тады вектары
- базіс ў ε n, тады вектары 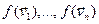 не ўтвараюць базіс ε n, значыцца, яны лінейна залежныя. Значыцца, існуюць
не ўтвараюць базіс ε n, значыцца, яны лінейна залежныя. Значыцца, існуюць 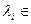 R не ўсе роўныя нулю, такія, што
R не ўсе роўныя нулю, такія, што 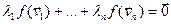 і
і 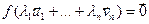 . З ін΄ектыўнасці f вынікае, што
. З ін΄ектыўнасці f вынікае, што 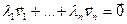 , а паколькі не ўсе каэфіцыенты
, а паколькі не ўсе каэфіцыенты 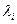 роўныя 0, гэта супярэчыць таму, што
роўныя 0, гэта супярэчыць таму, што 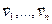 - базіс ε n. ■
- базіс ε n. ■
Ул-ць.15.3. Калі f: ε 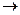 ε – артаганальны аператар, тады:
ε – артаганальны аператар, тады:
1) f захоўвае норму вектара (гэта значыць, што 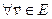
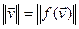 );
);
2) f захоўвае вугал паміж вектарамі
(гэта значыць, што 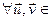 ε \{
ε \{ 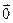 }
} 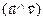 =
= 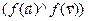 ).
).
Доказ. 1) 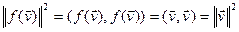 , значыцца
, значыцца 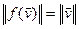 .
.
2) 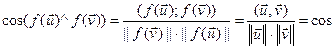
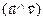 , адкуль
, адкуль 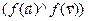 =
= 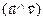 .■
.■
Ул-ць. 1 5.4. Лінейны аператар f: ε n 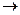 ε n з’яўляецца артаганальным тады і толькі тыды, калі для адвольнага ортаўнармаванага базіса
ε n з’яўляецца артаганальным тады і толькі тыды, калі для адвольнага ортаўнармаванага базіса 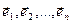 вектары
вектары 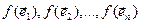 таксама ўтвараюць ортаўнармаваны базіс.
таксама ўтвараюць ортаўнармаваны базіс.
Доказ. 1) З таго, што 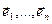 - ортаўнармаваны базіс па 15.3, атрымоўваем, што
- ортаўнармаваны базіс па 15.3, атрымоўваем, што 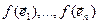 - таксама ортаўнармаваны базіс.
- таксама ортаўнармаваны базіс.
2) Няхай 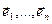 і
і 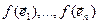 ортаўнармаваныя базісы ε n. Няхай вектары
ортаўнармаваныя базісы ε n. Няхай вектары 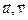 маюць у базісе
маюць у базісе 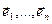 слупкі каардынат
слупкі каардынат 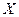 і
і 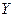 . З лінейнасці f вынікае, што
. З лінейнасці f вынікае, што 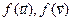 маюць таксама слупкі каардынат
маюць таксама слупкі каардынат 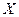 і
і 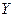 у базісе
у базісе 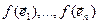 . Адсюль па 14.8 атрымоўваем, што
. Адсюль па 14.8 атрымоўваем, што 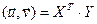 і
і 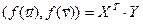 .■
.■
Азн.15.5. Матрвца A ÎMat(n´n;R) называецца артаганальнай, калі 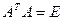 .
.
Прыклад.
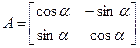
Лемма 15.6. Калі A, B ÎMat(n´n;R) і 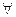 X, Y ÎRn
X, Y ÎRn 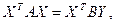 тады
тады 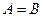 .
.
Доказ. 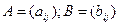 . Паколькі
. Паколькі 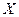 ,
, 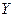 - адвольныя, разгледзім
- адвольныя, разгледзім 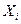 -слупок, у якога і -ы элемент роўны 1, а ўсе астатнія роўныя 0. Адпаведнв абазначым і
-слупок, у якога і -ы элемент роўны 1, а ўсе астатнія роўныя 0. Адпаведнв абазначым і 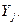 Нескладана ўбачыць, што
Нескладана ўбачыць, што 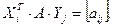 . З гэтага вынікае, што
. З гэтага вынікае, што 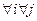
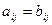 , значыцца,
, значыцца, 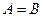 .■
.■
Ул-ць.15.7. Артаганальны аператар эўклідавай праторы ε n у ортаўнармаваным базісе мае артаганальную матрыцу.
Доказ. Няхай 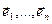 - ортаўнармаваны базіс ε n, f: ε n
- ортаўнармаваны базіс ε n, f: ε n 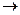 ε n – артаганальны аператар і А - яго матрыца ў гэтым базісе. Разгледзім адвольныя вектары
ε n – артаганальны аператар і А - яго матрыца ў гэтым базісе. Разгледзім адвольныя вектары 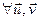 Î ε n, якія маюць слупкі каардынат
Î ε n, якія маюць слупкі каардынат 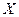 ,
, 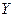 адпаведна ў дадзеным базісе. Тады вектары
адпаведна ў дадзеным базісе. Тады вектары 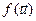 і
і 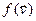 маюць слупкі каардынат
маюць слупкі каардынат 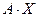 і
і 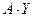 адпаведна. З артаганальнасці f па 14.7 вынікае, што
адпаведна. З артаганальнасці f па 14.7 вынікае, што
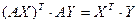 ,
, 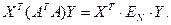
З лемы 15.6 вынікае, што 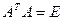 .■
.■
Ул-ць.15.8. Няхай у эўклідавай прасторы зададзены ортаўнармаваны базіс. Як вядома, кожнай матрыцы A ÎMat(n´n;R) адпавядае лінейны аператар f: ε n 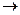 ε n, які ў гэтым базісе мае матрыцу А. Аператар f артаганальны тады і толькі тады, калі матрыца А артаганальная.
ε n, які ў гэтым базісе мае матрыцу А. Аператар f артаганальны тады і толькі тады, калі матрыца А артаганальная.
Доказ. (сам-на).
Ул-ць.15.9. Кампазіцыя артаганальных аператараў – артаганальны аператар.
Доказ. Няхай f: ε 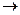 ε і g: ε
ε і g: ε 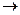 ε - артаганальныя, тады
ε - артаганальныя, тады 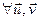 Î ε
Î ε
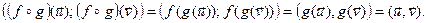 ■
■
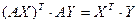 ,
, 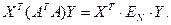
 2015-07-14
2015-07-14 309
309






