2.1. Вывести уравнение колебаний струны.
2.2. Используя уравнения Максвелла (система СИ)
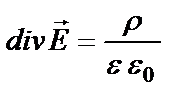 ,
, 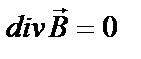 ,
, 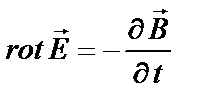 ,
, 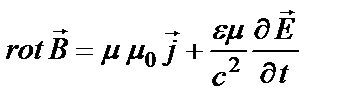
вывести волновое уравнение для электромагнитного поля в однородной среде – абсолютном диэлектрике (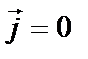 ) в отсутствие свободных зарядов (
) в отсутствие свободных зарядов (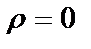 ).
).
Ответ. 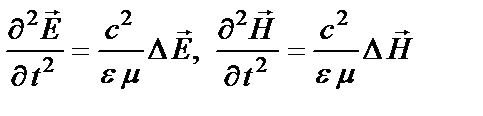 .
.
2.3 Вывести уравнение поперечных колебаний вращающейся струны длины l, конец которой закреплён на перпендикулярной к ней оси, зная угловую скорость вращения w и линейную плотность струны r.
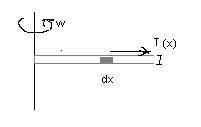 Указание. Сила натяжения струны
Указание. Сила натяжения струны 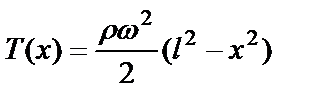
Ответ. 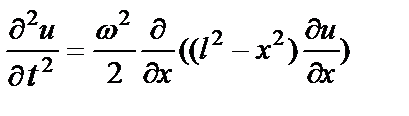
2.4. Вывести уравнение теплопроводности в стержне.
Указание. Количество тепла 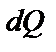 , проходящее через поперечное сечение стержня за время
, проходящее через поперечное сечение стержня за время 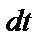 , выражается формулой
, выражается формулой 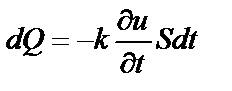 , где
, где 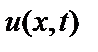 – температура в точке
– температура в точке 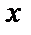 в момент
в момент 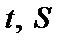 – площадь поперечного сечения стержня. Ответ.
– площадь поперечного сечения стержня. Ответ. 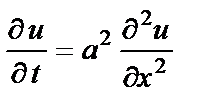 , где
, где 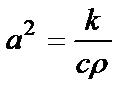 ,
, 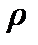 – плотность,
– плотность,  – удельная теплоёмкость.
– удельная теплоёмкость.
2.5. Вывести трёхмерное уравнение теплопроводности.
Указание. Использовать закон теплопроводности Фурье 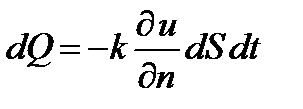 , где
, где 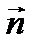 – единичный вектор внешней нормали к поверхности
– единичный вектор внешней нормали к поверхности 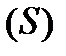 .
.
2.6. Вывести уравнение продольных колебаний однородного стержня с плотностью 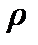 и площадью поперечного сечения
и площадью поперечного сечения 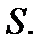
Указание. Обозначить через 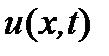 перемещение точки стержня с абсциссой
перемещение точки стержня с абсциссой 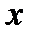 в момент времени
в момент времени 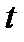 .
.
Найти относительное удлинение отрезка стержня от точки 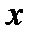 до точки
до точки 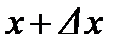 :
:
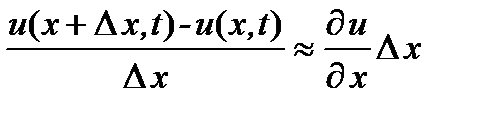 и применить закон Гука:
и применить закон Гука: 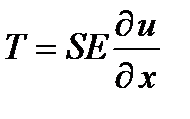 .
.
Ответ. 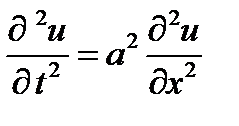 , где
, где 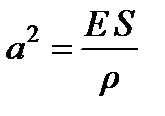 .
.
2.7. Однородный стержень плотности 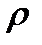 и длины
и длины 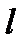 , закреплённый в точке
, закреплённый в точке 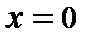 , растянут силой
, растянут силой 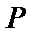 , приложенной к другому его концу. В момент времени
, приложенной к другому его концу. В момент времени 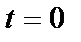 действие силы мгновенно прекращается. Сформулировать начальные и краевые условия.
действие силы мгновенно прекращается. Сформулировать начальные и краевые условия.
Указание. В момент 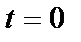 сила натяжения
сила натяжения 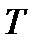 во всех сечениях стержня одна и та же и равна
во всех сечениях стержня одна и та же и равна 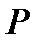 .
.
Ответ. 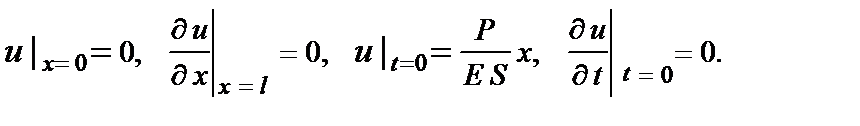
2.8 Вывести уравнение распространения звуковых колебаний в воздушной среде.
Ответ. 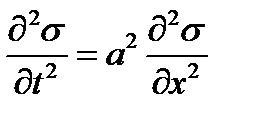 , где
, где  - относительное изменение плотности,
- относительное изменение плотности, 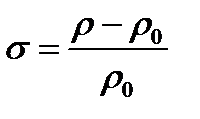 ,
,

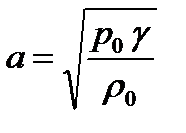 ,
, 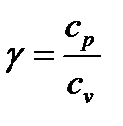 ,
, 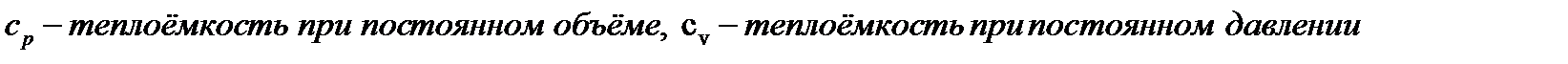
 2015-07-21
2015-07-21 392
392






