Примеры

Дифференциальные уравнения первого порядка

Дифференциальное уравнение первого порядка имеет вид

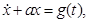(1)

где a – постоянный параметр, а 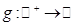- непрерывная функция.

Если a = 0, то решение x (t) уравнения (1) с начальным условием t = 0, x = x (0) представляется формулой

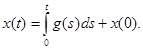
Решение однородного уравнения

Однородное уравнение, соответствующее дифференциальному уравнению (1) есть

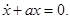(2)

Общее решение

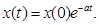(4)

Частное решение неоднородного уравнения

1.2.1. g (t) постоянная

В этом случае уравнение (1) имеет вид

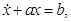(5)

где b – постоянный параметр.

Частное решение:

.

.

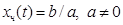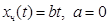Примеры

Пример 1.1. Пусть требуется решить неоднородное дифференциальное уравнение с заданным начальным условием

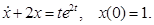(1.9)

Характеристическое уравнение однородной части имеет вид 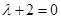поэтому общее решение соответствующего однородного уравнения есть

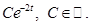
Частное решение исходного неоднородного уравнения ищем в виде 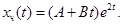Подставляя его у уравнение (1.9), получим

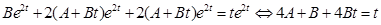
Поэтому приходим к системе уравнений для нахождения величин A и B

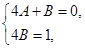
из которой находим B = 1 / 4, A = ‑ 1 / 16.

Таким образом, общее решение уравнения (1.9) имеет вид

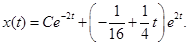(1.10)

Для определения произвольной постоянной C положим в формуле (1.10) t = 0, 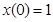. В результате будем иметь равенство

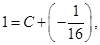(1.10)

из которого следует, что 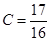. Следовательно, формула искомого решения дифференциального уравнения (1.9) принимает следующий вид

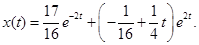(1.10)

Задание 1. Найти общее решение следующего дифференциального уравнения

1) ;

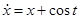2) ;

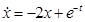3) ;

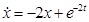4) ;

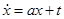5) ;

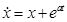Упражнения 1.1. 1) Найти решения следующих дифференциальных уравнений (для случая x (0) = 1)

(i) ,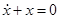

(ii) ,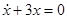

(iii) ;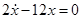

(iv) ;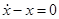

(v) ;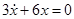

(vi) ;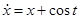

(vii) ;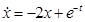

(viii) ;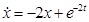

(ix) ;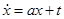

(x) ;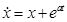

(xi)

2) Ввести в предыдущих примерах уравнений соответственно следующие неоднородные части (функцию)

(i) ;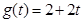

(ii) ;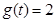

(iii) ;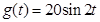

(iv) ;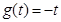

(v) ,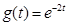

и определить общее решение полученного неоднородного уравнения.