Следствием правила умножения, и формулы полной вероятности является теорема гипотез или формула Байеса. По условиям опыта известно, что гипотезы H1, H2,…, Hn несовместны, образуют полную группу событий: Hi  Hj =
Hj =  при
при  и H1
и H1  H2,
H2,  ...,
...,  Hn =
Hn =  . Вероятности гипотез до опыта (так называемые «априорные вероятности») известны и равны P(H1), P(H2), …, P(Hn) = 1. Предположим, что опыт произведен и в результате появилось событие A. Спрашивается, как нужно пересмотреть вероятность гипотез с учетом этого факта, или, другими словами, какова вероятность того, что наступлению события A предшествовала гипотеза Hk (после опытные вероятности называются апостериорными): P(H1/A), P(H2/A), …, P(Hn/A). Вероятность наступления события A совместно с гипотезой Hk определяется с использованием теоремы умножения вероятностей: P(A
. Вероятности гипотез до опыта (так называемые «априорные вероятности») известны и равны P(H1), P(H2), …, P(Hn) = 1. Предположим, что опыт произведен и в результате появилось событие A. Спрашивается, как нужно пересмотреть вероятность гипотез с учетом этого факта, или, другими словами, какова вероятность того, что наступлению события A предшествовала гипотеза Hk (после опытные вероятности называются апостериорными): P(H1/A), P(H2/A), …, P(Hn/A). Вероятность наступления события A совместно с гипотезой Hk определяется с использованием теоремы умножения вероятностей: P(A  Hk) = P(Hk)
Hk) = P(Hk)  P(A / Hk) = P(A)
P(A / Hk) = P(A)  P(Hk / A). Таким образом, можно записать: P (Hk / A) = P (Hk)
P(Hk / A). Таким образом, можно записать: P (Hk / A) = P (Hk)  P(A / Hk) / P(A). С использованием формулы полной вероятности P(Hk/A) =
P(A / Hk) / P(A). С использованием формулы полной вероятности P(Hk/A) = 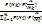 . Эта формула называется формулой Байеса. Она позволяет пересчитывать вероятности гипотез в свете новой информации, состоящей в том, что опыт дал результат А.
. Эта формула называется формулой Байеса. Она позволяет пересчитывать вероятности гипотез в свете новой информации, состоящей в том, что опыт дал результат А.
______________________________________________________________________
Теоремы о повторении опытов. Ф-ла Бернулли
9. Теоремы о повторении опытов. Формула Бернулли. Несколько опытов называются независимыми, если вероятность исхода опыта не зависит от того, какие исходы имели другие опыты. Рассмотрим случай, когда вероятности исходов опытов постоянны и не зависят от номера опыта. Пусть один и тот же опыт проводятся n раз. В каждом опыте некоторые события А1, А2, …, Аr появляется с вероятностями р1, р2, …, рп. Будем рассматривать не результат каждого конкретного опыта, а общее число появлений событий А1, А2, …, Аr. Рассмотрим случай с двумя возможными исходами опытов, т.е. в результате каждого опыта событие A появляется с вероятностью р и не появляется с вероятностью q=1-p. Вероятность P(n,k) того, что в последовательности из n опытов интересующее нас событие произойдет ровно k раз (безразлично, в какой последовательности), равна (формула Бернулли): 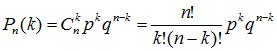 . Следствия из формулы Бернулли: Вероятность того, что событие А наступит менее k раз:
. Следствия из формулы Бернулли: Вероятность того, что событие А наступит менее k раз: 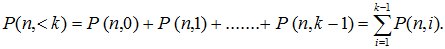
Вероятность того, что событие наступит более k раз: 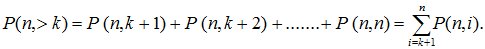 Вероятность того, что в n опытах схемы Бернулли, событие А появится от k1 до k2 раз
Вероятность того, что в n опытах схемы Бернулли, событие А появится от k1 до k2 раз 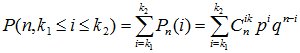
Вероятность того, что в n опытах событие А появится хотя бы один раз, определяется формулой 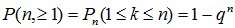 . Число k0, которому соответствует максимальная биномиальная вероятность Pn(k0), называется наивероятнейшим числом появления события А. При заданных n и p это число определяется неравенствами:
. Число k0, которому соответствует максимальная биномиальная вероятность Pn(k0), называется наивероятнейшим числом появления события А. При заданных n и p это число определяется неравенствами: 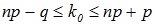 .
.
______________________________________________________________________
______________________________________________________________________
Случ. в-на, табл. задание распр. диск. случ. в-ны
10. Понятие случайной величины. Табличное задание закона распределения дискретной случайной величины.  Под случайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение. Возможные значения случайной величины образуют множество
Под случайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение. Возможные значения случайной величины образуют множество  , которое называется множеством возможных значений случайной величины. Обозначения случайной величины: X, Y, Z; возможные значения случайной величины: x, y, z. В зависимости от вида множества
, которое называется множеством возможных значений случайной величины. Обозначения случайной величины: X, Y, Z; возможные значения случайной величины: x, y, z. В зависимости от вида множества  случайные величины могут быть дискретными и непрерывными. С.В. Х называется дискретной, если множество ее возможных значений
случайные величины могут быть дискретными и непрерывными. С.В. Х называется дискретной, если множество ее возможных значений  – счетное или конечное. Если множество возможных значений С.В. несчетно, то такая С.В. является непрерывной. Законом распределения случайной величины называется соответствие между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения. Две случайные величины называются независимыми, если закон распределения одной из них не зависит то того, какие возможные значения приняла другая величина. В противном случае случайные величины называются зависимыми. Несколько случайных величин называются взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины. Закон распределения случайной величины может быть задан в виде таблицы, функции распределения либо плотности распределения. Таблица, содержащая возможные значения случайной величины и соответствующие вероят-ности, является простей-шей формой задания закона распределения случайной величины. Табличное задание закона распределения можно использовать только для дискретной случайной величины с конечным числом возможных значений. Табличная форма задания закона случайной величины называется также рядом распределения.
– счетное или конечное. Если множество возможных значений С.В. несчетно, то такая С.В. является непрерывной. Законом распределения случайной величины называется соответствие между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения. Две случайные величины называются независимыми, если закон распределения одной из них не зависит то того, какие возможные значения приняла другая величина. В противном случае случайные величины называются зависимыми. Несколько случайных величин называются взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины. Закон распределения случайной величины может быть задан в виде таблицы, функции распределения либо плотности распределения. Таблица, содержащая возможные значения случайной величины и соответствующие вероят-ности, является простей-шей формой задания закона распределения случайной величины. Табличное задание закона распределения можно использовать только для дискретной случайной величины с конечным числом возможных значений. Табличная форма задания закона случайной величины называется также рядом распределения.
______________________________________________________________________
Ф-я распределения случ. в-ны, ее свойства
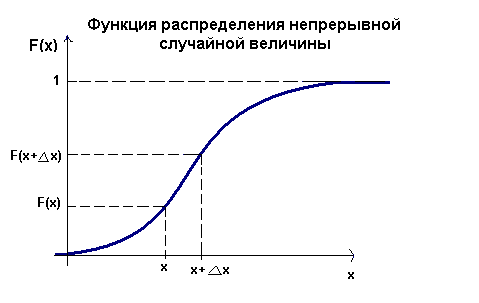
 11. Функция распределения случайной величины и ее свойства. Функцией распределения F(x) случайной величины X называется вероятность события, состоящего в том, что случайная величина X примет значение строго меньше аргумента этой функции, т.е. x. F(x)=P(X<x). С помощью функции распределения можно задавать закон распределения как дискретной, так и непре-рывной слу-чайной вели-чины. Для дискретной слу-чайной вели-чины ф-ция раз-рывная и ступенчатая, принимает значения от 1 до 0. Если случайная величина непрерывна, то функция распределения будет непрерывной неубывающей функцией, заключенной между 0 и 1. Свойства:
11. Функция распределения случайной величины и ее свойства. Функцией распределения F(x) случайной величины X называется вероятность события, состоящего в том, что случайная величина X примет значение строго меньше аргумента этой функции, т.е. x. F(x)=P(X<x). С помощью функции распределения можно задавать закон распределения как дискретной, так и непре-рывной слу-чайной вели-чины. Для дискретной слу-чайной вели-чины ф-ция раз-рывная и ступенчатая, принимает значения от 1 до 0. Если случайная величина непрерывна, то функция распределения будет непрерывной неубывающей функцией, заключенной между 0 и 1. Свойства:
0 ≤ F(x) ≤ 1,
F(x+  ) ≥ F(x)
) ≥ F(x)
F(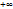 ) = 1
) = 1
F( ) = 0
) = 0
Если X непрерывна, то вероятность того, что она примет кон-кретные значения равна 0.
______________________________________________________________________
____________________________________________________________
Плотность распр. случ. в-ны, ее свойства
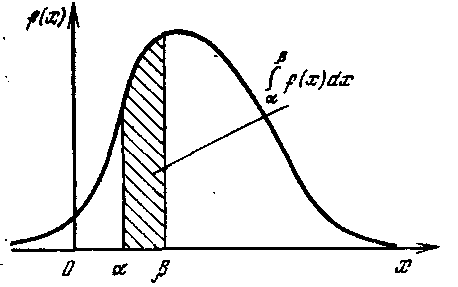 12. Плотность распределения случайной величины и ее свойства. С помощью плотности распределения можно задавать закон распределения только непре-рывной случайной величины. f(x) = F’(x) =
12. Плотность распределения случайной величины и ее свойства. С помощью плотности распределения можно задавать закон распределения только непре-рывной случайной величины. f(x) = F’(x) = 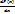 ; F(x) =
; F(x) = 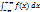 . Свойства: 1)F(x) ≥ 0; 2) P(a<x<b) =
. Свойства: 1)F(x) ≥ 0; 2) P(a<x<b) = 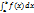 ,
, 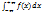 =1.
=1.
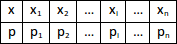 13. Математическое ожидание случайной величины и его свойства. Математическое ожидание характеризует положение случайной величины на числовой оси, определяет некоторое среднее значение, около которого сосредоточены все возможные значения этой случайной величины. Математическое ожидание часто называют средним значением случайной величины. M[x] – математическое ожидание x. Если случайная величина дискретна, т.е. задана в виде таблицы, то ее математич. ожидание: M[x]= mx = x1p1 + x2p2 + … + xipi + … + xnpn =
13. Математическое ожидание случайной величины и его свойства. Математическое ожидание характеризует положение случайной величины на числовой оси, определяет некоторое среднее значение, около которого сосредоточены все возможные значения этой случайной величины. Математическое ожидание часто называют средним значением случайной величины. M[x] – математическое ожидание x. Если случайная величина дискретна, т.е. задана в виде таблицы, то ее математич. ожидание: M[x]= mx = x1p1 + x2p2 + … + xipi + … + xnpn = 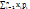 . Понятию математ. ожидания для дискретной случайной величины можно придать следующий физический смысл: Если приложить грузик, то вес будет равен вероятности. Если случайная величина непрерывна и ее закон распределения задан в виде плотности, то M[x] ]= mx =
. Понятию математ. ожидания для дискретной случайной величины можно придать следующий физический смысл: Если приложить грузик, то вес будет равен вероятности. Если случайная величина непрерывна и ее закон распределения задан в виде плотности, то M[x] ]= mx = 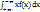 . Физический смысл: координата по оси X центра тяжести фигуры, ограниченной сверху графиком распределения. Свойства: 1) Мат.ож. константы = const. M[c] = c. 2) Мат. ожидание суммы двух случайных величин = сумме мат. ож. этих случайных величин, т.е. M[x+y] = M[x] + M[y], M[
. Физический смысл: координата по оси X центра тяжести фигуры, ограниченной сверху графиком распределения. Свойства: 1) Мат.ож. константы = const. M[c] = c. 2) Мат. ожидание суммы двух случайных величин = сумме мат. ож. этих случайных величин, т.е. M[x+y] = M[x] + M[y], M[ 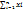 ] =
] = 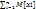 . 3) Если закон распределения случайной величины x никак не изменяется от того, какое значение приняла величина y (x и y независимы), то для таких случайных величин справедлива формула: M[xy] = M[x]M[y]. Следствие 1: M[cx] = cM[x]. След. 2: мат. ож. отклонения случайной величины от ее мат. ож. равно 0: M[x-M[x]] = 0. Случайная величина (x-M[x]) называется центрированной случайной величиной и обозначается x0.
. 3) Если закон распределения случайной величины x никак не изменяется от того, какое значение приняла величина y (x и y независимы), то для таких случайных величин справедлива формула: M[xy] = M[x]M[y]. Следствие 1: M[cx] = cM[x]. След. 2: мат. ож. отклонения случайной величины от ее мат. ож. равно 0: M[x-M[x]] = 0. Случайная величина (x-M[x]) называется центрированной случайной величиной и обозначается x0.
______________________________________________________________________
Дисперсия и среднее квадратичное отклонение
14. Дисперсия и среднее квадратичное отклонение, их свойства. Эти числовые характеристики показывают насколько велико рассеивание случайной величины относительно среднего значения этой случайной величины. Dx = D[x] =  = M[
= M[ 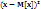 ] равно: 1)
] равно: 1) 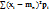 - для дискретных; 2)
- для дискретных; 2) 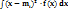 - для непрерывных. Важное: 1) Дисперсия всегда больше 0; 2.) Ее размерность – квадрат размерности случайной величины. Чтобы сделать так, чтобы размерность случайной величины x и размерность числовой характеристики, определя-ющей величину разброса случайной величины относительно среднего значения, совпадала, рассмо-трим корень квадратный из дисперсии.
- для непрерывных. Важное: 1) Дисперсия всегда больше 0; 2.) Ее размерность – квадрат размерности случайной величины. Чтобы сделать так, чтобы размерность случайной величины x и размерность числовой характеристики, определя-ющей величину разброса случайной величины относительно среднего значения, совпадала, рассмо-трим корень квадратный из дисперсии. 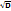 =
=  наз. средним квадратичным отклонением. Свойства: 1) Дисперсии константы есть константа. D[c]=0; 2) Постоянный множитель случайной величины можно выносить за знак дисперсии, предварительно возведя его в квадрат D[cx]=c2D[x]; 3) Если случайные величины независимы D[x+y] = D[x]+D[y]; D[x-y] = D[x+(-1)y] = D[x] + D[(-1)y] = D[x]+D[y]; 4) Дисперсия случайной величины равна разности между мат. ож. квадрата случайной величины и квадратом мат. ож. этой случайной величины. D[x] = M[x2] – M2[x]; D[x] = M[(x-mx)2] = M[x2-2mxx+mx2] = M[x2] – M[2mxx] + M[mx2] = M[x2] - 2mxM[x] + mx2= M[x2] - mx2 = M[x2] – M2[x]. Свойство 4 позволяет упростить вычисление дисперсии.
наз. средним квадратичным отклонением. Свойства: 1) Дисперсии константы есть константа. D[c]=0; 2) Постоянный множитель случайной величины можно выносить за знак дисперсии, предварительно возведя его в квадрат D[cx]=c2D[x]; 3) Если случайные величины независимы D[x+y] = D[x]+D[y]; D[x-y] = D[x+(-1)y] = D[x] + D[(-1)y] = D[x]+D[y]; 4) Дисперсия случайной величины равна разности между мат. ож. квадрата случайной величины и квадратом мат. ож. этой случайной величины. D[x] = M[x2] – M2[x]; D[x] = M[(x-mx)2] = M[x2-2mxx+mx2] = M[x2] – M[2mxx] + M[mx2] = M[x2] - 2mxM[x] + mx2= M[x2] - mx2 = M[x2] – M2[x]. Свойство 4 позволяет упростить вычисление дисперсии.
______________________________________________________________________
______________________________________________________________________
Мода, медиана, моменты случайных величин
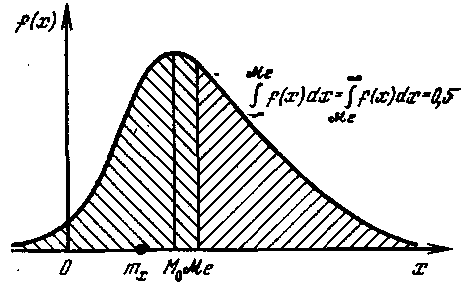 15. Мода, медиана и моменты случайных величин. Модой Mo дискретной случайной величины называется наиболее вероятное ее значение. Для непрерывной случайной величины модой называется такое значение, при котором плотность принимает наибольшее значение. Для непрерывной случайной величины медианой Ме называется такое значение случайной величины, для которого справедливо следующее равенство:
15. Мода, медиана и моменты случайных величин. Модой Mo дискретной случайной величины называется наиболее вероятное ее значение. Для непрерывной случайной величины модой называется такое значение, при котором плотность принимает наибольшее значение. Для непрерывной случайной величины медианой Ме называется такое значение случайной величины, для которого справедливо следующее равенство: 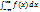 =
= 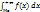 =
=  . Для случайной величины мода и медиана могут быть различны.
. Для случайной величины мода и медиана могут быть различны.
 Если график сим-метричен отно-сительно прямой || Oy, проходящей через Ме, то мат. ожидание, мода Мо и медиана Ме совпадают. Обобщением м. ожид. и дисп. явл. момент. Моментом К-го порядка наз. мат. ожидание сл. в-ны Z=(x-a)k; νk(a) = M[(x-a)k], k=1,2,..; a=0 – мо-мент началь-ный, a=mx – мо-мент центральный,
Если график сим-метричен отно-сительно прямой || Oy, проходящей через Ме, то мат. ожидание, мода Мо и медиана Ме совпадают. Обобщением м. ожид. и дисп. явл. момент. Моментом К-го порядка наз. мат. ожидание сл. в-ны Z=(x-a)k; νk(a) = M[(x-a)k], k=1,2,..; a=0 – мо-мент началь-ный, a=mx – мо-мент центральный,  – начальный момент,
– начальный момент,  1 = M[x];
1 = M[x];  2 = M[x2];
2 = M[x2];  3 = M[x3].
3 = M[x3].  k = M[(x-mx)k] – центральный момент,
k = M[(x-mx)k] – центральный момент,  1 = M[(x-mx)] = 0,
1 = M[(x-mx)] = 0,  2 = M[(x-mx)2] = Dx,
2 = M[(x-mx)2] = Dx,  3 = M[(x-mx)3]. Дисперсию можно выразить через моменты следующим образом:
3 = M[(x-mx)3]. Дисперсию можно выразить через моменты следующим образом:  2 =
2 =  2 -
2 -  12. Можно доказать справедливость следующих формул:
12. Можно доказать справедливость следующих формул:  3 =
3 =  3 - 3
3 - 3  2
2  1 + 2
1 + 2  13,
13,  4 =
4 =  4 - 4
4 - 4  3
3  1 +6
1 +6  2
2  1 -3
1 -3  14. Третий центральный момент
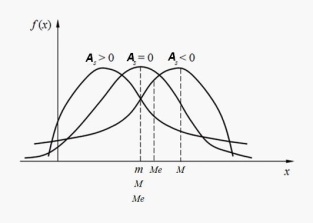
14. Третий центральный момент  3 служит для характеристики асимметрии распределения. Для этого используют коэффициент асимметрии As = µ3/
3 служит для характеристики асимметрии распределения. Для этого используют коэффициент асимметрии As = µ3/  3. Четвертый центральный момент
3. Четвертый центральный момент  4 служит для характе-ристики крутости или островершинности распреде-ления. Для этого используют коэффициент Ex называемый эксцессом: Ex = (
4 служит для характе-ристики крутости или островершинности распреде-ления. Для этого используют коэффициент Ex называемый эксцессом: Ex = ( 4/
4/  4)-3.
4)-3.
______________________________________________________________________
Биномиальный и Пуассона з-ны распределения
16. Биномиальный закон распределения и его свойства. Производится n независимых опытов, в каждом из которых может наступить или не наступить событие A, где вероятность наступления события A: P(A) = p, а вероятность того, что событие А не наступит т.е. обратного события  : P(
: P( ) = 1 – p = q; Тогда вероятность того что событие А, в n независимых опытах, наступит ровно m раз определяется формулой Бернулли:
) = 1 – p = q; Тогда вероятность того что событие А, в n независимых опытах, наступит ровно m раз определяется формулой Бернулли: 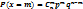 , где
, где 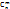 – число сочетаний из n по m, x - случайная величина равная количеству появлений события А. Так как формула Бернулли является формулой для членов разложения бинома
– число сочетаний из n по m, x - случайная величина равная количеству появлений события А. Так как формула Бернулли является формулой для членов разложения бинома 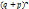 , то такое распределение вероятностей называется биномиальным. М. ожидание:
, то такое распределение вероятностей называется биномиальным. М. ожидание: 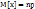 ; Дисперсия:
; Дисперсия: 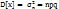 . Биномиальное распре-деление применяется для дискретных величин, однако при большом количестве опытов приближается к нормальному распределению (согласно Центральной предельной теоремы).
. Биномиальное распре-деление применяется для дискретных величин, однако при большом количестве опытов приближается к нормальному распределению (согласно Центральной предельной теоремы).
17. Закон распределения Пуассона. Закон распределения Пуассона получается из биномиального закона распределения, если число испытаний “m” неограниченно возрастает при одновременном уменьшении вероятности наступления “p”, причем “np = const”. 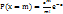 , где a = np = const – параметр закона распределения Пуассона. Мат. ожидание:
, где a = np = const – параметр закона распределения Пуассона. Мат. ожидание: 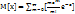 =
= 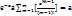 (тут получившаяся сумма сходится к экспоненте в степени а и всё сокращается). Дисперсия: Т.к.
(тут получившаяся сумма сходится к экспоненте в степени а и всё сокращается). Дисперсия: Т.к. 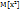 =
= 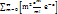 =
= 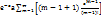 =
= 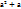 , то D[x] =
, то D[x] = 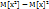 =
=  = a. Равенство математического ожидания и дисперсии является одной из особенностей распределения Пуассона, эта особенность часто применяется в математической статистике. Распределением Пуассона можно пользоваться, когда исследуемая величина подчинена биномиальному закону распределения, но при этом известно, что “m” – достаточно большое, а “p” достаточная мала.
= a. Равенство математического ожидания и дисперсии является одной из особенностей распределения Пуассона, эта особенность часто применяется в математической статистике. Распределением Пуассона можно пользоваться, когда исследуемая величина подчинена биномиальному закону распределения, но при этом известно, что “m” – достаточно большое, а “p” достаточная мала.
______________________________________________________________________
_________________________________________________________________________
Равномерное и экспоненциальное распр.
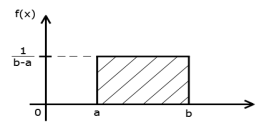
18. Равномерное и экспоненциальное распределения. Равномерное распределение для дискретных величин. Если случайная величина Х принимает конечное число значений с равными вероятностями, то вероятность одного (любого) события A (х = m) равна 1/n, где n – число опытов. Математическое ожидание: 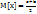 , где а – начальное возможное значение, b – конечное. Дисперсия:
, где а – начальное возможное значение, b – конечное. Дисперсия: 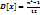 ; Равномерное распре-деление для непрерывных величин. Говорят что случайная величина Х имеет равномерное распределение если:Х может принимать любые значения на интервале [a, b];в каждой точке интервала [a, b] значение плотности распределения одно и тоже. Плотность распределения: f(x) =
; Равномерное распре-деление для непрерывных величин. Говорят что случайная величина Х имеет равномерное распределение если:Х может принимать любые значения на интервале [a, b];в каждой точке интервала [a, b] значение плотности распределения одно и тоже. Плотность распределения: f(x) = 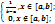
 Функция распределения: F(x) =
Функция распределения: F(x) = 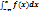 =
= 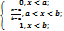
Мат. ожидание: M[x] = 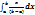 =
= 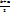 ; Дисперсия: D[x] =
; Дисперсия: D[x] = 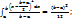 Показательное распре-деление. О случайной величине Х говорят, что она подчинена экспоненциальному (показательному) распределению, если она принимает только положительные значения и её ф-я плотности распре-деления имеет следующий вид: f(x) =
Показательное распре-деление. О случайной величине Х говорят, что она подчинена экспоненциальному (показательному) распределению, если она принимает только положительные значения и её ф-я плотности распре-деления имеет следующий вид: f(x) = 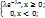
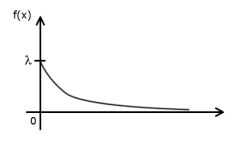 Ф-я распределения: F(x) =
Ф-я распределения: F(x) = 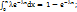 Мат. ожидание: M[x] =
Мат. ожидание: M[x] = 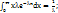 Дисперсия: D[x] =
Дисперсия: D[x] = 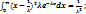
______________________________________________________________________
Нормальный закон распределения, его св-ва
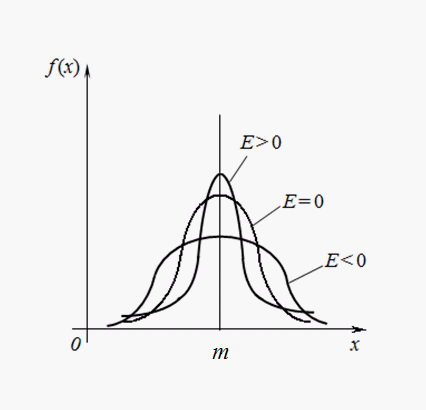
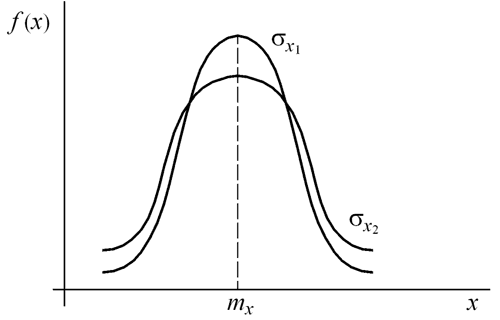 19. Нормальный закон распределения и его свойства. Нормальный закон распределения является наиболее часто встречающимся на практике законом распределения. Его главная особенность состоит в том что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
19. Нормальный закон распределения и его свойства. Нормальный закон распределения является наиболее часто встречающимся на практике законом распределения. Его главная особенность состоит в том что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. 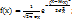 На практике часто необходимо выяснить вероятность того, что нормально распреде-ленная случайная ве-личина находится в пределах интервала. P(a<X<b) =
На практике часто необходимо выяснить вероятность того, что нормально распреде-ленная случайная ве-личина находится в пределах интервала. P(a<X<b) = 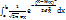 =
= 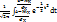 . Данный интеграл не выражается через элементарные функции для его расчета используют табличные функции:
. Данный интеграл не выражается через элементарные функции для его расчета используют табличные функции: 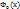 =
= 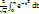 или
или 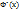 =
= 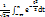 ;
; 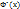 – является ф-ей распределения нормально распределенной случайной величины с
– является ф-ей распределения нормально распределенной случайной величины с 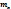 = 0, a
= 0, a  = 1.
= 1. 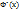 =
= 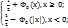
P(a<X<b) = 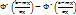 . Если нормально рас-пределенная случайная величина принимает значения в интервале длинной L симметричном относительно мат. ожидания, то её вероятность можно рассчитать по формуле: P =
. Если нормально рас-пределенная случайная величина принимает значения в интервале длинной L симметричном относительно мат. ожидания, то её вероятность можно рассчитать по формуле: P = 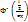 -
- 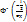 =
= 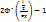 =
= 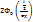 . Правило 3-х сигм. Основываясь на формуле выше можно показать, что практически все возможные значения равно распределенной величины находятся в интервале
. Правило 3-х сигм. Основываясь на формуле выше можно показать, что практически все возможные значения равно распределенной величины находятся в интервале  ;
; 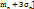 . Правило 3-х сигм позволяет вычислить приближенно неизвестное значение среднего квадратического отклонения или дисперсии по результатам опытов (экспериментально).
. Правило 3-х сигм позволяет вычислить приближенно неизвестное значение среднего квадратического отклонения или дисперсии по результатам опытов (экспериментально).
______________________________________________________________________
____________________________________________________________
С-мы случ. в-н, табл. способ задания з-на распр.
20. Системы случайных величин, табличный способ задания закона распределения. Системой случайных величин называют комплекс нескольких случайных величин, которые в совокупности характеризуют результат опыта и рассматриваются совместно. В общем случае закон распределения случайной величины полностью не исчерпывается законами распределения компонент этой системы, т.к. изменение значений одной компоненты может изменить законы распределения других компонентов. Система случ. в-н обозначаются как: 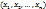 . Сист. с. в. можно интерпретировать как некую точку в n-мерном пространстве, или как n-мерный случайный вектор. Табличный способ задания закона распределения (на примере системы 2-ух случайных величин). Если компоненты системы являются дискретными с. в., то закон распределения можно задать с помощью таблицы следующего вида (для сист. 2-ух с.в.):
. Сист. с. в. можно интерпретировать как некую точку в n-мерном пространстве, или как n-мерный случайный вектор. Табличный способ задания закона распределения (на примере системы 2-ух случайных величин). Если компоненты системы являются дискретными с. в., то закон распределения можно задать с помощью таблицы следующего вида (для сист. 2-ух с.в.):
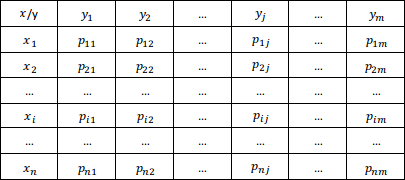
 =
= 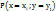 . Т.к. в результате опыта каждая из компонент принимает одно и только одно из возможных значений, то:
. Т.к. в результате опыта каждая из компонент принимает одно и только одно из возможных значений, то: 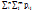 = 1;
= 1; 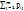 =
=  ;
; 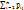 =
= 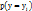 . Знание закона распределения системы однозначно дает возможность получить закон распределения компонент системы по отдельности.
. Знание закона распределения системы однозначно дает возможность получить закон распределения компонент системы по отдельности.
______________________________________________________________________
Совм. ф-я распределения с-мы 2 случ. в-н, св-ва
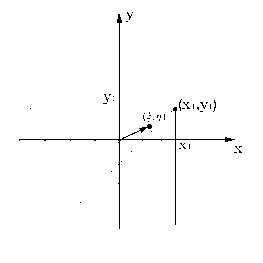 21. Совместная функция распределения системы двух случайных величин, ее свойства. Функцией распределения системы из двух случ. в-н (X,Y) называется вероятность совместного выполнения двух неравенств X<x и Y<y: F(X,y) = P((X<x)(Y<y)). По определению, функция распределения F(x,y) есть вероятность попадания случайной точки с координатами (x,y) в квадрат с бес-конечными разме-рами, расположенный левее и ниже этой точки на плоскости XOY. Отдельно для каждой случ. в-ны X и Y можно определить одномерную функцию распре-деления, например, F1(x) есть вероятность попадания в полуплоскость, расположенную левее точки с координатой x. Также и F1(y) есть вероятность попадания в полуплоскость ниже точки y. Свойства:
21. Совместная функция распределения системы двух случайных величин, ее свойства. Функцией распределения системы из двух случ. в-н (X,Y) называется вероятность совместного выполнения двух неравенств X<x и Y<y: F(X,y) = P((X<x)(Y<y)). По определению, функция распределения F(x,y) есть вероятность попадания случайной точки с координатами (x,y) в квадрат с бес-конечными разме-рами, расположенный левее и ниже этой точки на плоскости XOY. Отдельно для каждой случ. в-ны X и Y можно определить одномерную функцию распре-деления, например, F1(x) есть вероятность попадания в полуплоскость, расположенную левее точки с координатой x. Также и F1(y) есть вероятность попадания в полуплоскость ниже точки y. Свойства:
1) 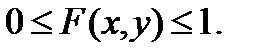
2) 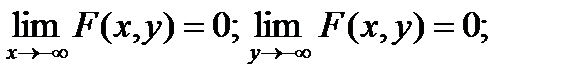
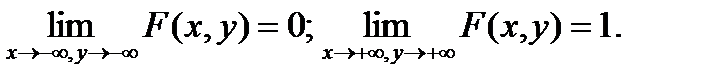
3) 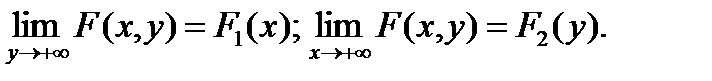
4) F(x,y) неубывающая функция по каждому аргументу при фиксированном втором
5) 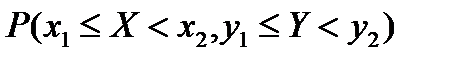 =
= 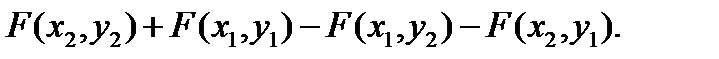
6) 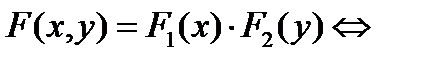 X и Y независимые с. в.
X и Y независимые с. в.
7) F(x,y) = 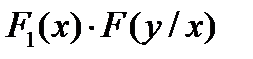 =
= 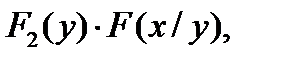 где F(x/y), F(y/x) – условные функции распределения.
где F(x/y), F(y/x) – условные функции распределения.
В текстовом виде: 2) на -  по обеим осям она равна нулю; 3) при равенстве
по обеим осям она равна нулю; 3) при равенстве 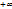 одного из аргументов согласно другому аргументу она превращается в одномерную функцию распределения; 4) F(x,y) есть неубывающая функция обоих своих аргументов; 5) если оба аргумента равны +¥, то F(x,y) = 1. Вероятность попадания случайной точки в квадрат R с координатами (α,β) по оси x и (γ,δ) по оси y равна
одного из аргументов согласно другому аргументу она превращается в одномерную функцию распределения; 4) F(x,y) есть неубывающая функция обоих своих аргументов; 5) если оба аргумента равны +¥, то F(x,y) = 1. Вероятность попадания случайной точки в квадрат R с координатами (α,β) по оси x и (γ,δ) по оси y равна 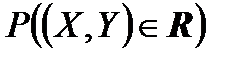 =
= 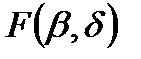 -
- 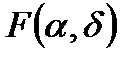 -
- 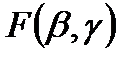 +
+ 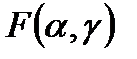 . F(x,y) существует как для непрерывных, так и для дискретных СВ.
. F(x,y) существует как для непрерывных, так и для дискретных СВ.
______________________________________________________________________
____________________________________________________________
Совм. пл-ть распределения с-мы 2 сл. в-н, св-ва
22. Совместная плотность распределения системы двух случайных величин, ее свойства. Пусть у функции F2(x,y) существуют производные по x и y, а также вторая смешанная производная. Совместной (или двумерной) плотностью распределения вероятностей случайных величин  и
и  наз. ф-я f2(x,y) =
наз. ф-я f2(x,y) = 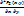 . Свойства двумерной плотности вероятности: 1) Справедливо соот-е: P(
. Свойства двумерной плотности вероятности: 1) Справедливо соот-е: P(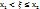 ,
,  ) =
) = 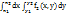 . Для док-ва исп. раенство, тогда:
. Для док-ва исп. раенство, тогда: 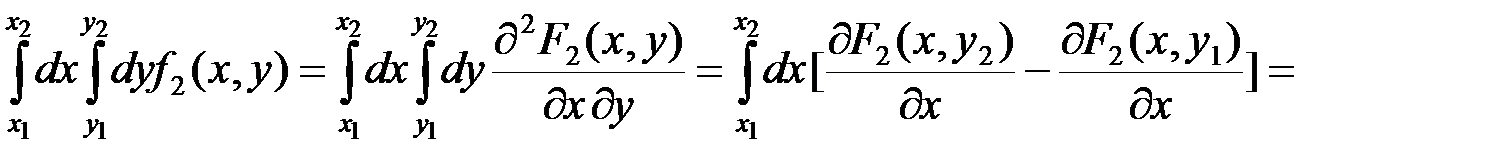
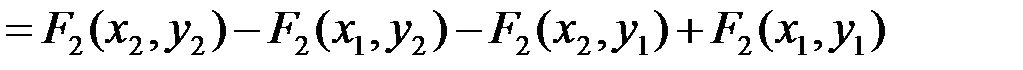 . Это соот-ношение имеет практическое значение, поскольку позволяет выч-ть вероятность
. Это соот-ношение имеет практическое значение, поскольку позволяет выч-ть вероятность 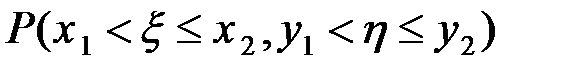 попадания двумерного вектора (ξ,η) в прямоугольник, определяемый отрезками (x1,x2] и (y1,y2] через пл-ть вероятности f2(x,y). 2) Рассмотрим частный случай соотношения. Пусть x1=-
попадания двумерного вектора (ξ,η) в прямоугольник, определяемый отрезками (x1,x2] и (y1,y2] через пл-ть вероятности f2(x,y). 2) Рассмотрим частный случай соотношения. Пусть x1=-  , x2=x, y1=-
, x2=x, y1=-  , y2=y, тогда формула принимает вид: F2(x,y) =
, y2=y, тогда формула принимает вид: F2(x,y) = 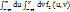 . Это соотношение определяет функцию распределения вероятностей F2 через плотность вероятности f2.
. Это соотношение определяет функцию распределения вероятностей F2 через плотность вероятности f2.
3. Рассмотрим при условиях: x1=-  , x2=
, x2=  , y1=-
, y1=-  , y2=
, y2=  , тогда следует равенство:
, тогда следует равенство: 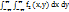 , поскольку
, поскольку 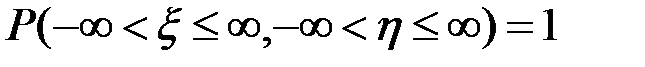 как вероятность досто-верного события. Это соотношение называется условием нормировки для плотности вероятности f2. 4. Если f2 - плотность вероятности вектора (ξ, η), и fξ – пл-ть в-ти случ. величины ξ, то
как вероятность досто-верного события. Это соотношение называется условием нормировки для плотности вероятности f2. 4. Если f2 - плотность вероятности вектора (ξ, η), и fξ – пл-ть в-ти случ. величины ξ, то 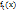 =
= 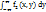 . Это равенство называется свойством согласованности плотности второго порядка f2 и плотности первого порядка fξ. Если известна плотность второго порядка f2, то по формуле можно вычислить плотность вероятности fξ - случайной величины ξ. Аналогично,
. Это равенство называется свойством согласованности плотности второго порядка f2 и плотности первого порядка fξ. Если известна плотность второго порядка f2, то по формуле можно вычислить плотность вероятности fξ - случайной величины ξ. Аналогично, 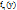 =
= 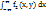 . Доказательство получим на основе равенства F2(x,
. Доказательство получим на основе равенства F2(x,  ) = Fξ(x). Представим F2 через плотность f2, а Fξ через fξ, тогда следует
) = Fξ(x). Представим F2 через плотность f2, а Fξ через fξ, тогда следует 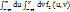 =
= 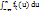 . Дифференцирование по x приводит к равенству, что и завершает доказательство. 5. Случайные величины и называются независимыми, если независимы случайные события
. Дифференцирование по x приводит к равенству, что и завершает доказательство. 5. Случайные величины и называются независимыми, если независимы случайные события 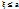 и
и 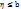 при любых числах a и b. Для независимых случайных величин
при любых числах a и b. Для независимых случайных величин  и
и  :
: 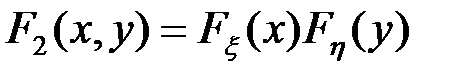 . Доказательство следует из определений функций F2 и Fξ, Fη. Поскольку
. Доказательство следует из определений функций F2 и Fξ, Fη. Поскольку  и
и  - независимые случайные величины, то события вида:
- независимые случайные величины, то события вида: 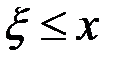 и
и 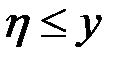 - независимые для любых x и y. Поэтому
- независимые для любых x и y. Поэтому 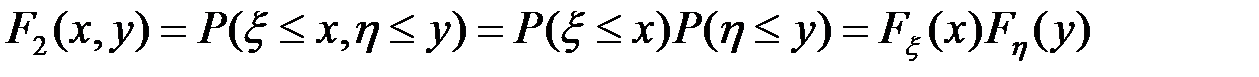 .
.
Продифференцируем по x и y, тогда согласно получаем следствие для плотностей: 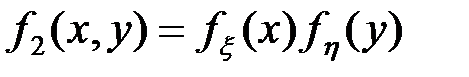 . 6. Пусть G - произвольная область на плоскости (x,y), тогда
. 6. Пусть G - произвольная область на плоскости (x,y), тогда 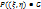 =
= 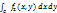 - вероятность того, что вектор (ξ,η) принимает любые значения из области G определяется интегралом по G от плотности вероятности f2. Рассмотрим пример случайного вектора (ξ,η) с равномерным распределением вероятностей, который имеет плотность вероятности f2(x,y)=λ на прямо-угольнике a<x≤b, c<y≤d и f2(x,y)=0 - вне этого прямоугольника. Число λ определяется из условия нормировки:
- вероятность того, что вектор (ξ,η) принимает любые значения из области G определяется интегралом по G от плотности вероятности f2. Рассмотрим пример случайного вектора (ξ,η) с равномерным распределением вероятностей, который имеет плотность вероятности f2(x,y)=λ на прямо-угольнике a<x≤b, c<y≤d и f2(x,y)=0 - вне этого прямоугольника. Число λ определяется из условия нормировки: 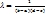 .
.
______________________________________________________________________
____________________________________________________________
Числовые хар-ки сис-мы 2 случайных величин
23. Числовые характеристики системы двух случайных величин. Числовые характеристики непрерывно распределённой системы случайных величин Х, У. Начальный момент порядка k+S равен
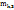 =
= 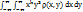 . Математическими ожиданиями называются начальные моменты первого порядка m1,0 = mx = M[x] =
. Математическими ожиданиями называются начальные моменты первого порядка m1,0 = mx = M[x] = 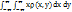 ; m0,1 = my = M[Y] =
; m0,1 = my = M[Y] = 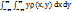 . Центральный момент порядка k+S равен μk,S =
. Центральный момент порядка k+S равен μk,S = 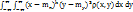 . Центральные моменты второго порядка μ2,0 = Dx = D[x], μ0,2 = Dy = D[y] называются дисперсиями, μ1,1 = Kxy = cov(X,Y) называется ковариацией. Нормированная ковариация rxy =
. Центральные моменты второго порядка μ2,0 = Dx = D[x], μ0,2 = Dy = D[y] называются дисперсиями, μ1,1 = Kxy = cov(X,Y) называется ковариацией. Нормированная ковариация rxy = 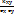 называется коэффициентом корреляции системы двух случайных величин. Среднеквадратичные отклонения: σx =
называется коэффициентом корреляции системы двух случайных величин. Среднеквадратичные отклонения: σx = 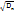 и σy =
и σy = 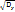 . Числовые характеристики дискретно распределённой системы случайных величин Х, У: Начальный момент порядка k+S равен: mk,S =
. Числовые характеристики дискретно распределённой системы случайных величин Х, У: Начальный момент порядка k+S равен: mk,S = 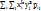 . Математическими ожиданиями называются начальные моменты первого порядка m1,0 = mx = M[x] =
. Математическими ожиданиями называются начальные моменты первого порядка m1,0 = mx = M[x] = 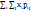 =
= 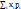 . Центральный момент порядка k+S равен μk,S =
. Центральный момент порядка k+S равен μk,S = 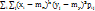 . m0,1 = my = M[Y] =
. m0,1 = my = M[Y] = 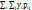 =
= 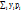 . Центральные моменты второго порядка: μ2,0 = Dx = D[x] =
. Центральные моменты второго порядка: μ2,0 = Dx = D[x] = 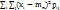 =
= 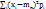 =
= 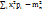 , μ2,0 = Dx = D[x] (далее аналогично) - называются дисперсиями. Центральный момент второго порядка μ1,1 = Kxy = cov(X,Y) =
, μ2,0 = Dx = D[x] (далее аналогично) - называются дисперсиями. Центральный момент второго порядка μ1,1 = Kxy = cov(X,Y) = 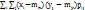 =
= 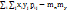 называется ковариацией. Нормированная ковариация rxy =
называется ковариацией. Нормированная ковариация rxy = 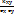 называется коэффициентом корреляции системы двух случайных величин. Среднеквадратичные отклонения: σx =
называется коэффициентом корреляции системы двух случайных величин. Среднеквадратичные отклонения: σx = 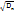 и σy =
и σy = 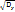 .
.
______________________________________________________________________
Усл. з-ны распр., зав., незав. случ. в-ны, т-ма умн.
24. Условные законы распределения случайных величин, зависимые и независимые случайные величины, теорема умножения законов распределения. Условным законом распределения называется распределение одной случайной величины, найденное при условии, что другая случайная величина приняла определенное значение. Условные ряды вероятностей для дискретных составляющих Х и Y определяются по формулам: pi / j = P(X = xi / Y = yj) = pij /P(Y = yj) = 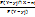 =
= 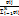 , i = 1,..., N; pj / i = P(Y = yj / X = xi)= pij /P(X = xi)=
, i = 1,..., N; pj / i = P(Y = yj / X = xi)= pij /P(X = xi)= 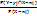 =
= 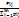 , j= 1,…,M
, j= 1,…,M
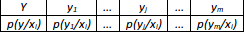 Условное распре-деление может быть предста-влено в виде таблицы. Заметим, что
Условное распре-деление может быть предста-влено в виде таблицы. Заметим, что 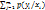 =
= 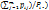 =
= 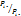 = 1. Условные плотности для непрерывных составляющих X и Y определяются так
= 1. Условные плотности для непрерывных составляющих X и Y определяются так
f (x / y) = f (x, y)/ f у(y), f у (y)¹ 0; f (y / x) = f (x, y)/ f х(x), f х (x)¹ 0.
Fx(x/y) = (Fx(x/y))x’ = f(x,y)/fy(y); FY(y/x) = (FY(y/x))y’ = f(x,y)/fx(x). Условные плотности обладают всеми свойствами обычных плотностей: двумерная плотность вероятности неотрицательна f(x,y)  0; условие нормировки
0; условие нормировки 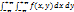 =1;
=1; 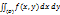 =1.
=1.
Величина Х не зависит от величины Y, если ее закон распределения не зависит от того, какое значение приняла величины Y. Для независимых величин выполняется следующие соотношения: 1) F (x, y) = p (X < x, Y < y) = p (X < x) p (Y < y) = FX (x) FY (y); 2) для непр. случ. величин f (x, y) = f 1(x) f 2(y); 3) для дискретных случайных величин pij = pi pj, для " i, j. Для независимых величин двумерные формы закона распределения не содержат никакой дополнительной информации кроме той, которая содержится в двух одномерных законах. В случае зависимости величин Х и Y, переход от двух одномерных законов к совместному осуществить невозможно. Для этого необходимо знать условные законы распределения.
______________________________________________________________________
____________________________________________________________
Нормальный закон распределения
25. Нормальный закон распределения системы двух случайных величин. Непрерывная двумерная случайная величина (X,Y) имеет нормальное распределение, если ее совместная плотность вероятности имеет вид: f(x,y) = 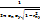
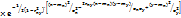 ,где mx – мат. ожид. случайной величины X, my – мат. ожид. случ. величины Y, σx – среднее квадратичное отклонение с. в. X, σy – среднее квадратичное отклонение с. в. Y, rxy – коэффициент корреляции. Условные законы распределения с. в. X и Y также явл. нормальными:
,где mx – мат. ожид. случайной величины X, my – мат. ожид. случ. величины Y, σx – среднее квадратичное отклонение с. в. X, σy – среднее квадратичное отклонение с. в. Y, rxy – коэффициент корреляции. Условные законы распределения с. в. X и Y также явл. нормальными: 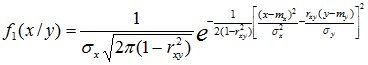
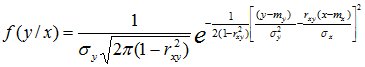
Условные числовые характеристики имеют вид: 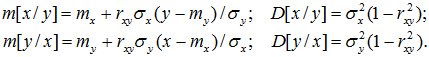
Для системы нормально распределенных случайных величин линии регрессии m[x/y] и m[y/x] представляют собой прямые линии, т.е. регрессия линейна. Для двумерной норм. распр. с. в. – если составляющие не коррелированы, то они и независимы, т.е. rxy=0: 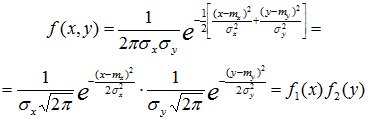
Итак, для нормально распределенных составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны. Можно показать, что двумерная случайная величина (Х,Y) распределена нормально, то Х и Y связаны линейной корреляционной зависимостью.
______________________________________________________________________
____________________________________________________________
Системы n-случайных величин
 26. Системы n – случайных величин. Упорядоченный набор (
26. Системы n – случайных величин. Упорядоченный набор (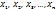 ) случайных величин
) случайных величин  (
(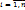 ), заданных в одном и том же поле случайных величин
), заданных в одном и том же поле случайных величин  , называется
, называется 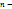 мерной случайной величиной или системой
мерной случайной величиной или системой  случайных величин. Одномерные случайные величины
случайных величин. Одномерные случайные величины 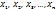 называются компонентами или составляющими
называются компонентами или составляющими 
 мерной случайной величины (
мерной случайной величины (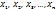 ). Их удобно рассматривать как координаты случайной точки или случайного вектора
). Их удобно рассматривать как координаты случайной точки или случайного вектора 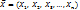 в пространстве
в пространстве 
 измерений. На многомерные случайные величины распространяются почти все основные понятия и определения, относящиеся к одномерным случайным величинам. Рассмотрим двумерную случайную величину (X, Y). Упорядоченная пара (X, Y) двух случайных величин X и Y называется двумерной случайной величиной или системой двух одномерных случайных величин X и Y. Систему (X, Y) можно изобразить случайной точкой M(X, Y) или случайным вектором
измерений. На многомерные случайные величины распространяются почти все основные понятия и определения, относящиеся к одномерным случайным величинам. Рассмотрим двумерную случайную величину (X, Y). Упорядоченная пара (X, Y) двух случайных величин X и Y называется двумерной случайной величиной или системой двух одномерных случайных величин X и Y. Систему (X, Y) можно изобразить случайной точкой M(X, Y) или случайным вектором 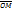 . Система (X, Y) – функция элементарного события (X, Y)
. Система (X, Y) – функция элементарного события (X, Y) 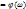 . Каждому
. Каждому  ставится в соответ-ствие два действи-тельных числа x и y - значения X и Y. В этом случае
ставится в соответ-ствие два действи-тельных числа x и y - значения X и Y. В этом случае 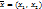 назыв. реализацией вектора
назыв. реализацией вектора 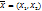 . Системы случайных величин могут быть дискретными, непрерывными и смешанными в зависимости от образующих систему случайных величин. Полной харакиеристикой системы (X, Y) является её закон распределения вероятностей, указывающий область возможных значений системы случайных величин и вероятность этих значений. Закон распределения (X, Y):
. Системы случайных величин могут быть дискретными, непрерывными и смешанными в зависимости от образующих систему случайных величин. Полной харакиеристикой системы (X, Y) является её закон распределения вероятностей, указывающий область возможных значений системы случайных величин и вероятность этих значений. Закон распределения (X, Y): 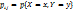
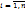
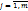 (или может быть задан в виде таблицы, изображенной ниже).
(или может быть задан в виде таблицы, изображенной ниже).  Сумма всех вероятностей
Сумма всех вероятностей  , как сумма вероятностей полной группы несовместных событий: {X=x;Y=y}=1,
, как сумма вероятностей полной группы несовместных событий: {X=x;Y=y}=1, 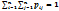 . Зная закон распределения двумерной дискретной случайной величины можно найти законы распределения каждой из компонент, причем обратное не верно.
. Зная закон распределения двумерной дискретной случайной величины можно найти законы распределения каждой из компонент, причем обратное не верно. 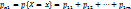 , что следует из теории сложения несовместных событий {X=
, что следует из теории сложения несовместных событий {X=  , Y=
, Y=  }, {X=
}, {X=  , Y=
, Y=  }, …, {X=
}, …, {X=  , Y=
, Y=  }.
}.  налогично находим:
налогично находим: 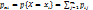 и
и 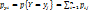 .
.
______________________________________________________________________
Ф-я случ. в-н, нах-е ч. хар-к ф-и по з. з-нам р. арг.
 27. Понятие функции случайных величин. Нахождение числовых характеристик функции случайных величин по заданным законам распределения аргументов. Если каждому возможному значению случайной величины X по определенному правилу соответствует одно возможное значение случайной величины Y, то Y – называется функцией случайного аргумента X,
27. Понятие функции случайных величин. Нахождение числовых характеристик функции случайных величин по заданным законам распределения аргументов. Если каждому возможному значению случайной величины X по определенному правилу соответствует одно возможное значение случайной величины Y, то Y – называется функцией случайного аргумента X,  . Пусть Х – дисперсная случайная величина с возможными значениями
. Пусть Х – дисперсная случайная величина с возможными значениями  вероятности которых равны соответственно
вероятности которых равны соответственно  , т.е.
, т.е. 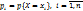 . Очевидно, что случайная величина
. Очевидно, что случайная величина  , также дисперсная случайная величина, с возможными значениями
, также дисперсная случайная величина, с возможными значениями 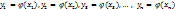 , вероятности которых соответственно равны
, вероятности которых соответственно равны  , т.е. если
, т.е. если 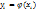 , то
, то 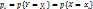 ,
, 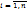 . Возможные значения случайной величины X могут соответствовать одинаковым значениям случайной величины Y. Вероятности повторяющихся значений складываются. Пример нахождения числовых характеристик функции по закону распределения аргумента: Найти MY, если: а)
. Возможные значения случайной величины X могут соответствовать одинаковым значениям случайной величины Y. Вероятности повторяющихся значений складываются. Пример нахождения числовых характеристик функции по закону распределения аргумента: Найти MY, если: а) 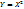 ; б)
; б) 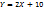 .
.
 а) Случ. в-на Y принимает значения
а) Случ. в-на Y принимает значения 
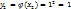 ,
, 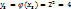 . Таким образом, она принимает значения 1 и 4, причем
. Таким образом, она принимает значения 1 и 4, причем 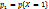 =
= 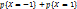 = 0.1 + 0.3 = 0.4,
= 0.1 + 0.3 = 0.4, 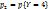 =
= 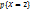 = 0.6. MY =
= 0.6. MY =  = 2.8. б) Закон распределения Y имеет вид таблицы, изобр. слева. MY=
= 2.8. б) Закон распределения Y имеет вид таблицы, изобр. слева. MY= 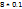 +
+ 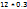 +
+ 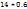 =12.8.
=12.8.
______________________________________________________________________
____________________________________________________________
Опр. числ. хар-к и з-нов р. ф-ий с. в. по аргументу
28-29. Определение числовых характеристик функции случайных величин по заданным числовым характеристикам аргументов. Определение законов распределения функций случайных величин по заданным законам распределения аргументов. Рассмотрим случайную величину Y, зависящую функционально от случайной величины X с известным законом распределения F(x): Y = 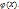 Если Х – дискретная случайная величина и известен ее ряд распределения имеет вид:
Если Х – дискретная случайная величина и известен ее ряд распределения имеет вид: 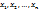 ,
, 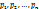 . Определяем вероятности появления различных значений случайной величины Y:
. Определяем вероятности появления различных значений случайной величины Y: 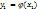 ,
, 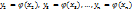 . Тогда мат. ожид. случайной величины Y определяется так:
. Тогда мат. ожид. случайной величины Y определяется так: 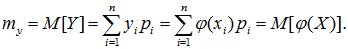
Если случ. в-на X непрерывна и имеет плотность распр-я f(x), то заменяя в формуле вер-ти pi элементом вероятности f(x)dx, а сумму – интегралом, получаем: 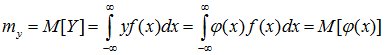
Для смешанной случайной величины выражение для математического ожидания преобразуется к виду: 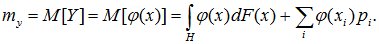
Эти соотношения – общее понятие мат. ожидания, позволяющее вычислить мат. ожидание для неслучайных функций случайного аргумента. Например, дисперсия случ. величины Y=φ(x) определяется так: 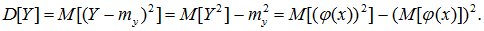
Величину M[φ(x)] рассчитываем в соответствии с первыми тремя формулами. Для определения математического ожидания квадрата φ(х) воспользуемся следующими соотношениями: 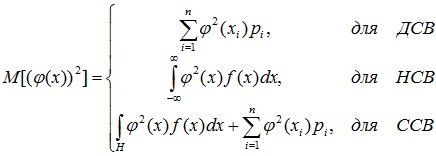
Таким образом, для нахождения числовых характеристик функции Y=φ(x) достаточно знать закон распределения ее аргумента.
______________________________________________________________________
Характеристические ф-ии и их основные св-ва
30. Определение и основные свойства характерис-тических функций. Характеристической функцией случайной величины X называется матем. ожидание случайной величины  , обозначаемое
, обозначаемое 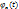 или
или 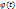 .
.
По определению  . Для дисперсии случайной величины X, принимающей значения
. Для дисперсии случайной величины X, принимающей значения  с вероятностью
с вероятностью 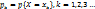 характерна формула
характерна формула 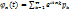 . Для непрерывной случайной величины с плотностью f(x):
. Для непрерывной случайной величины с плотностью f(x): 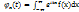 . Характеристическая функция непрерывной случайной величины есть преобразование Фурье от ее плотности f(x). f(x) выраженная через
. Характеристическая функция непрерывной случайной величины есть преобразование Фурье от ее плотности f(x). f(x) выраженная через 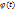 образует обратное преобразование Фурье:
образует обратное преобразование Фурье: 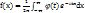 . Если случайная величина принимает целочисленные значения 0, 1, 2, …, то
. Если случайная величина принимает целочисленные значения 0, 1, 2, …, то  , где
, где 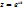

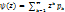 . Свойства характеристических функций: 1) Для всех
. Свойства характеристических функций: 1) Для всех 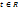 имеет место нер-во:
имеет место нер-во: 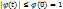 . 2) Если
. 2) Если 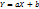 , где
, где 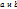 постоянные, то
постоянные, то 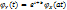 . Характеристическая функция суммы двух независимых случайных величин X и Y равна произведению их характеристических функций
. Характеристическая функция суммы двух независимых случайных величин X и Y равна произведению их характеристических функций 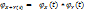 . Если для некоторого k существует начальный момент k-го порядка случайной величины X, т.е.
. Если для некоторого k существует начальный момент k-го порядка случайной величины X, т.е. 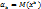 , то существует k-я производная характеристической функции и ее значение при t = 0 равно
, то существует k-я производная характеристической функции и ее значение при t = 0 равно
 2015-08-12
2015-08-12 947
947