Симплекс-метод решения задач линейного программирования

1. Симплекс-метод как обобщение графического.

2. Каноническая форма задачи ЛП.

3. Идея алгоритма симплекс-метода.

4. Вычислительный алгоритм симплекс-метода.

Обобщение графического метода решения приводит к алгебраическому симплекс-методу. Графический способ решения задачи ЛП показывает, что оптимальное решение этой задачи всегда ассоциируется с угловой (крайней) точкой пространства решений. Это является ключевой идеей при разработке общего алгебраического симплекс-метода для решения любой задачи линейного программирования [1].

Переход от геометрического способа решения задачи ЛП к симплекс-методу лежит через алгебраическое описание крайних точек пространства решений. Для реализации этого перехода сначала надо привести задачу ЛП к канонической форме, преобразовав неравенства ограничений в равенства путем введения дополнительных переменных.

Каноническая форма позволяет алгебраически получить базисные решения, (используя систему уравнений, порожденную ограничениями). Эти базисные решения полностью определяют все крайние точки пространства решений.

Каноническаяформа записи задачи ЛП предполагает выполнение следующих требований: все ограничения преобразуются в равенства с неотрицательной правой частью и все переменные неотрицательные.

Каноническая форма записи задач линейного программирования имеет вид:

Z= с₁х₁ + с₂х₂ +... + с_пх_п ® mах (целевая функция).

a₁₁х₁ + a₁₂x₂ + … + a_1nx_n = b₁
a₂₁х₁ + a₂₂x₂ + … + a_2nx_n = b_{2
………………………………………………….} (система ограничений)
a_m1х₁ + a_m2x₂ + … + a_mnx_n = b_m

х_i ≥ 0, i = 1,2, …, n (ограничения на переменные).

bj ≥ 0, j = 1,2,…,m (неотрицательные правые части ограничений)

Ее матричный вид:

C X ® max,
A X = B,
Х ≥ 0, B ≥ 0/

Все задачи ЛП можно привести к каноническому виду, руководствуясь следующими правилами.

1. Минимизация целевой функции Z равносильна максимизации целевой функции (-Z). Так, если целевая функция исходной задачи исследуется на минимум, т.е. Z®min, то можно рассмотреть функцию с противоположным знаком, которая будет стремиться к максимуму: -Z®max.

2. Неравенства любого типа (со знаками неравенств ≤ или ≥) можно преобразовать в равенства путем добавления в левую часть неравенств дополнительных переменных остаточных или избыточных.

Для неравенств типа ≤ в левую часть неравенства вводится неотрицательная остаточная переменная. Например, в модели ограничение на количество сырья задается в виде неравенства 6х₁ + 4х₂ ≤ 24. Вводя новую неотрицательную переменную s₁, которая показывает остаток (неиспользованное количество) сырья это ограничение преобразуется в равенство

6х₁ + 4х₂ + s₁ = 24, s₁≥0.

Неравенства типа ≥ в задачах ЛП обычно устанавливают нижнюю границу чего-либо. Избыточная переменная определяет превышение значения левой части неравенства над этой границей. Так, в модели диеты неравенство x₁ + х₂ ≥ 800 показывает, что суточное производство пищевой добавки не должно быть меньше 800 фунтов. Математически это неравенство эквивалентно равенству

х, + х₂ – S₁ = 800, S₁≥0.

Положительное значение избыточной переменной S₁ показывает превышение суточного производства добавки над минимальным значением в 800 фунтов. Важно еще раз подчеркнуть, что дополнительные переменные – остаточная s₁ и избыточная S₁ – всегда неотрицательные.

3. Правую часть равенства всегда можно сделать неотрицательной, умножив все равенство на –1. Кроме того, заметим, что неравенство типа ≤ также преобразуется в неравенство типа ≥ посредством умножения обеих частей неравенства на –1.

Например, неравенство –х₁, + х₂ ≤ –3 эквивалентно равенству

–х₁ + х₂ + s₁ = –3, s₁≥0.

Теперь, умножая обе части этого равенства на –1, получим равенство с неотрицательной правой частью: х₁ – х₂ – s₁ = 3.

4. Преобразование неположительных переменных в неотрицательные:

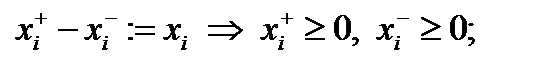
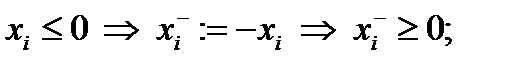
причем одну из двух переменных x_i^- или x_i⁺ можно полагать равной нулю. Например, если x=3, то ее можно представить в виде x_i⁺=3, x_i^- =0. Если x=-5, то x_i⁺=0, x_i^- =-5. Такие преобразования должны быть выполнены во всех неравенствах и целевой функции. После решения задачи с переменными x_i^- и x_i⁺ значения исходных переменных восстанавливаются с помощью обратной подстановки.

Основное свойство симплекс-метода заключается в том, что решение задачи ЛП осуществляется итерационно. На каждой итерации алгоритм переходит к новой угловой точке, которая потенциально может улучшить значение целевой функции.

Идеи, лежащие в основе графического метода решения задач линейного программирования, также являются основой и алгебраического симплекс-метода.

В графическом методе пространство решений определяется как пересечение полупространств, порождаемых ограничениями. В симплекс-методе пространство решений задают система из m линейных уравнений и n неотрицательных переменных.

Пространство решений графического метода, имеющее бесконечное число точек решений. В алгебраическом представлении задачи ЛП количество уравнений m всегда меньше или равно количеству переменных n. Если m = n и система уравнений совместна, то она имеет только одно решение; если же m<n и система уравнений совместна, то она имеет бесконечное множество решений. Простая иллюстрация в качестве доказательства: для уравнения х = 2 имеем m = n = 1, а его решение, очевидно, единственное. Для уравнения х + у = 1 имеем m = 1 и n = 2, этому уравнению удовлетворяет бесконечное множество решений (любая точка на прямой х + у = 1 будет решением).

Как уже говорилось, что базисные решения полностью определяют все крайние точки пространства решений. Тогда решение может быть найдено путем перебора всех допустимых базисных решений, что неэффективно.

Алгоритм симплекс-метода находит оптимальное решение, рассматривая ограниченное количество допустимых базисных решений. Алгоритм начинается с некоторого допустимого базисного решения и затем пытается найти другое базисное решение, улучшающее значение целевой функции.

В алгебраическом представлении кандидаты на оптимальное решение (т.е. те же угловые точки в графическом представлении) определяются из системы линейных уравнений следующим образом. Пусть m < n, тогда полагаем (n – m) переменных равными нулю и решаем систему из m уравнений относительно оставшихся m переменных.

Это положение иллюстрирует следующий пример.

Максимизировать Z = 2х₁ + Зх₂

при выполнении условий

2х₁+x₂≤4,

,

х_l, x₂≥0.

На рис. 1.10 показано пространство решений для этой задачи.

B

C

D

А

х1

х2

2х1+x2=4

х1 + 2х2=5

Рис. 1.10. Пространство решений

После преобразования к канонической форме имеем следующую задачу ЛП.

Максимизировать Z = 2х₁ + Зх₂

при выполнении условий

2х₁ +х₂ + s₁ = 4,

х₁ + 2х₂ + s₂ = 5,

х₁ х₂, s₁,s₂>0.

Здесь имеем систему из m = 2 уравнений для n = 4 переменных. Согласно сформулированному выше правилу угловые точки можно определить алгебраически, присвоив n-m=4-2=2 переменным нулевых значений и решив затем систему уравнений относительно оставшихся m = 2 переменных. Если, например, положить х₁ = 0 и х₂ = 0, тогда решением системы будет s₁ = 4, s₂ = 5. Это решение соответствует точке A на рис. 1.10. Другую угловую точку можно определить, если положить s₁ = 0 и s₂ = 0. В этом случае надо найти решение системы

2х₁ +х₂ = 4,

x₁ + 2х₂ = 5.

Решением в данном случае будет х₁ = 1 и х₂ = 2, что соответствует точке С на рис. 1.10.

Основываясь на графическом методе оптимальное решение задачи линейного программирования можно найти путем простого перебора всех базисных (допустимых) решений. Но, конечно, такая процедура не эффективна. Алгоритм симплекс-метода находит оптимальное решение, рассматривая ограниченное количество допустимых базисных решений.

Обычно алгоритм симплекс-метода начинается с исходной точки А, где х₁ = х₂ = 0 (рис. 1.10). В этой начальной точке значение целевой функции Z равно нулю. Возникает естественный вопрос: если одна или обе небазисные переменные х₁ и х₂ примут положительные значения, то приведет ли это к улучшению (возрастанию) значений целевой функции? Для ответа на этот вопрос рассмотрим целевую функцию максимизировать Z = 2х₁ + Зх₂.

Очевидно, что если переменная х₁ или переменная х₂ (или обе сразу) примут положительные значения, то это приведет к увеличению значения целевой функции. Однако алгоритм симплекс-метода на каждом шаге допускает изменение значения только одной небазисной переменной.

1. Если увеличивать значение переменной x₁, то (см. рис. 1.10) ее значение должно возрасти таким образом, чтобы соответствовать угловой точке В (повторим, что внутренние точки отрезка от точки А до точки В неприемлемы, поскольку кандидатом на оптимальное решение может быть только угловая точка). В точке В симплекс-метод должен увеличить значение переменной х₂, перемещаясь при этом в угловую точку С. Так как точка С соответствует оптимальному решению, то на этом процесс вычислений заканчивается. Таким образом, алгоритм симплекс-метода создает путь А–В–С.

2. Если сначала увеличивать значение переменной х₂, то следующей угловой точкой будет точка D, из которой процесс решения переходит в оптимальную точку С. Здесь алгоритм симплекс-метода создает путь А–D–C.

Отметим, что оба пути A–B–C и A–D–C расположены вдоль границы пространства решений. Это означает, что симплекс-метод не может сразу перескочить из точки А в точку С.

Может возникнуть правомерный вопрос: существует ли правило, в соответствии с которым можно было бы определить, какую небазисную переменную сделать положительной в данной угловой точке? Например, в точке А как переменная x₁ так и переменная х₂ могут увеличить значение целевой функции.

Симплекс-метод предлагает простое правило выбора переменных, которое в основном применяется в его программных реализациях. Поскольку здесь мы рассматриваем задачу максимизации, то следует выбирать такую небазисную переменную, которая имеет наибольший положительный коэффициент в выражении целевой функции. Если таких переменных несколько, то выбор произвольный. Необходимо понимать, что это эмпирическое правило, сформулированное на основе многочисленных компьютерных вычислений симплекс-метода – в большинстве случаев (но не обязательно всегда) применение этого правила ведет к наименьшему числу итераций, затрачиваемых на поиск оптимального решения.

Процесс перевода небазисных переменных в базисные и наоборот при переходе от одной угловой точки к следующей. На рис. 1.10 показано, что в точке А переменные s₁ и s₂ являются базисными, а переменные x₁ и х₂ – небазисными. Если переменная х₁ принимает положительное значение, мы переходим в угловую точку В, в которой изменяется состояние переменной x₁ из небазисной в базисную. Одновременно переменная s₁, которая была базисной в точке А, становится небазисной и принимает нулевое значение в точке В. Здесь существенно, что происходит одновременный "обмен состояниями" между небазисной переменной х₁ и базисной переменной s₁, что приводит к новым базисным переменным (x₁, s₂) и небазисным переменным (s₁, x₂) в точке В. Скажем, что в точке А переменная x₁ вводится в базисное решение, а переменная s₁ – исключается из базисного решения. В соответствии с терминологией симплекс-метода выбранная небазисная (нулевая) переменная называется вводимой (в базисное решение), а удаляемая (из базисного решения) базисная переменная – исключаемой. В точке В вводимой и исключаемой переменными будут соответственно переменные х₂ и s₂. Процесс изменения состояний переменных заканчивается в точке С, поскольку найдено оптимальное решение.

Рассмотрим вычислительный алгоритм симплекс-метода на следующем примере [Петров].

Предприятие производит два вида продукции. Для производства единицы первого продукта требуется 2 часа ручной сборки и 1 час машинной сборки. Для производства единицы второго продукта требуется 1 час ручной сборки и 3 часа машинной сборки. Ежедневно в распоряжении предприятия имеется 40 часов для ручной сборки и 45 часов для машинной сборки. Рыночные условия не позволяют продавать более 12 единиц первого продукции ежедневно. Прибыль от реализации единицы первого продукта составляет 300 грн., второго – 250 грн.

Целью предприятия является выбор такого ассортиментного набора, при котором достигается максимум прибыли в день.

Задача линейного программирования имеет вид:

целевая функция Z = 300x₁ + 250x₂ ® max,

ограничения

2x₁ + 1х₂ ≤ 40 (на время ручной сборки),

1x₁ + 3х₂ ≤ 45 (на время машинной обработки),

1x₁ + 0х₂ ≤ 12 (рыночный спрос на продукцию),

x₁ ≥ 0, х₂ ≥ 0.

Запишем задачу в каноническом виде. Для этого в каждое ограничение введем остаточные переменные 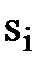(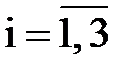). Эти же переменные войдут в целевую функцию с нулевыми коэффициентами.

Z = 300x₁ + 250x₂ 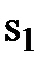+ 0 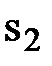+ 0 + 0 ,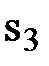

2x₁ + 1х₂ + 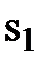=40,

1x₁ + 3х₂ + 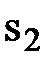=45,

1x₁ + 0х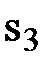₂ + =12,

x₁ ≥ 0, х₂ 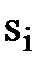≥ 0, ≥ 0 ().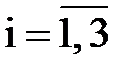

Шаг 1. Построение симплекс-таблицы.

Представим коэффициенты, стоящие в левой части системы уравнений, в табличной форме (табл. 1.3). За обозначения столбцов примем переменные, которым они соответствуют. Значения правой части ограничений запишем в отдельном столбце таблицы справа. За обозначения строк примем обозначения соответствующих переменных, которые являются базисными переменными в начальной крайней точке (начале координат х₁=0, х₂=0). Введем в таблицу дополнительную строку, соответствующую коэффициентам целевой функции Z. Существует несколько отличных друг от друга алгоритмов решения задачи симплекс-методом. В том из них, который излагается ниже, требуется вводить коэффициенты целевой функции с отрицательным знаком.

Таблица 1.3. Первая симплекс-таблица

Базисные переменные	Переменные	Правая часть b
х1	х2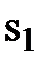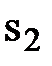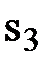
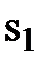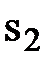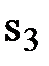Z	-300	-250

Шаг 2. Установка вводимой базисной переменной.

В строке коэффициентов целевой функции Z (табл. 1.4) найдем наибольшее отрицательное значение (-300). Столбец, соответствующий этому значению называется ведущим и переменная х₁ будет вводимой в базисное решение (выделен серым цветом). Разделим соответствующие значения правой части на соответствующие значения ведущего столбца. Затем разделим все элементы ведущей строки на ведущий элемент (1). В результате получим столбец отношений (табл. 1.4).

Таблица 1.4. Первая симплекс-таблица с учетом отношений

Базисные переменные	Переменные	Правая часть b	Отношения: b/элемент ведущего столбца
x1	х2	s1	s2	s3
s1							40/2=20
s2							45/1=45
s3							12/1=12
Z	-300	-250

Шаг 3. Установка исключаемой базисной переменной.

Выберем среди полученных отношений наименьшее положительное отношение. В нашем случае оно равно 12 (табл. 1.4). Соответствующая ему строка 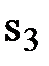является ведущей и переменная s₃ будет исключающей из базисного решения (выделена серым цветом). Пересечение ведущего столбца и ведущей строки дает ведущий элемент 1.

Шаг 4. Замена базисных переменных.

Обозначение ведущей строки s₃ заменим на обозначение ведущего столбца х₁ (табл. 1.5). Новые переменные соответствующие обозначениям строк это базисные переменные второго базисного решения.

Шаг 5. Выполнение арифметических преобразований.

Применив к строкам таблицы арифметические операции (строчные операции в матричной алгебре), приведем все остальные элементы ведущего столбца к нулю. В качестве базиса в этих арифметических операциях должна использоваться только ведущая строка.

Выполним следующие операции (результат см. табл.1.5):

1. Строка х₁ = старая строка s₃.

2. Новая строка s₁ = старая строка s₁ – 2 старая строка s₃.

3. Новая строка s₂ = старая строка s₂ – 1 старая строка s₃.

4. Новая строка Z = старая строка Z – (-300) старая строка s₃.

Таблица 1.5. Вторая симплекс-таблица с учетом отношений

Базисные переменные	Переменные	Правая часть b	Отношения: b/элемент ведущего столбца
x1	х2	s1	s2	s3
s1					-2		16/1=16
s2					-1		33/3=11
х1							12/0=∞
Z		-250

Шаг 6. Проверка базисного решения на оптимальность.

Шаги 2-5 повторяются до тех пор, пока не будет достигнута неотрицательность всех элементов в строке целевой функции Z.

Поскольку в данном случае есть отрицательный элемент в строке целевой функции, перейдем к третьей итерация (третьому базисному решению).

Выберем в полученной таблице ведущий столбец и вычислим затем новые значения в столбце отношений. Затем разделим все элементы ведущей строки на ведущий элемент 3 (табл. 1.6).

Таблица 1.6. Вторая симплекс-таблица с измененной ведущей строкой

Базисные переменные	Переменные	Правая часть b	Отношения: b/элемент ведущего столбца
x1	х2	s1	s2	s3
s1					-2		16/1=16
s2				1/3	-1/3		11/1=11
х1							12/0=∞
Z		-250

Выполним следующие операции:

1. Строка x₂ = старая строка s₂.

2. Новая строка s₁ = старая строка s₁ – 1 старая строка s₂.

3. Новая строка s₃ = старая строка s₃ – 0 старая строка s₂.

4. Новая строка Z = старая строка Z – (-250) старая строка s₂.

Обозначение ведущей строки s₂ заменим на обозначение ведущего столбца x₂.

Таблица 1.7. Третья, итоговая, симплекс-таблица.

Базисные переменные	Переменные	Правая часть b
x1	х2	s1	s2	s3
s1				-1/3	-5/3		Свободный ресурс-ручной труд
x2				1/3	-1/3		Количество второго продукта
х1							Количество первого продукта
Z				250/3	650/3		Максимальное значение прибыли

Теперь все элементы в строке целевой функции либо положительны, либо равны нулю, следовательно, представленное в данной таблице решение является оптимальным.

Проанализируем данные, которые получены в ходе построения итоговой симплекс-таблицы.

Базисными называются переменные, которые имеют ненулевые значения в крайней точке допустимого множества. Их значения находятся в соответствующих строках столбца b. Следовательно, оптимальным планом производства является:

х₁ = 12 единиц в день,

х₂ = 11 единиц в день,

а значение остаточной переменной s₁, соответствующей времени для ручной сборки составило 5 часов в день (этот избыток времени можно использовать для производства другого вида продукции).

Все остальные переменные имеют нулевые значения. Это означает, что данные ограничения являются дефицитными, а ресурсы, соответствующие времени для машинной сборки и ежедневной квоте продаж изделий х₁ расходуются полностью. Оптимальное значение целевой функции указано в строке Z столбца b. Максимальное значение получаемой ежедневно прибыли составляет 6350 грн.

Элементы, стоящие на пресечении строки целевой функции и столбцов остаточных переменных s₁, s₂, s₃ соответствуют теневым ценам (коэффициентам Лагранжа) ресурсов. Теневая цена ресурса время машинной сборки составляет 250/3 грн. за 1час, а теневая цена для ресурса ручной обработки – 650/3 грн. за одну единицу. Это означает, что если при производстве продукции использовать на 1 час машинной сборки больше нормативного значения (в нашем примере 45 часов), то ежедневная прибыль возрастет на 250/3≈83.33 грн. (минус любые дополнительные издержки) и составит 6350+250/3≈6433.33 грн. Иначе говоря, если в исходной модели задачи ограничение 1x₁ + 3х₂ + 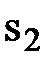≤ 45 заменить на неравенство 1x₁+ 3х₂ + 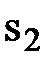≤ 46, ежедневная прибыль увеличиться на 250/3 грн. Аналогичным образом, если увеличится количество продаж изделия х₁ на 1 единицу сверх нормы (в нашем примере 12 единиц), то ежедневная прибыль возрастет на 650/3 грн. (минус любые дополнительные издержки).

Подробный анализ чувствительности решения задачи линейного программирования проводится обычно с помощью стандартных пакетов прикладных программ.

Литература

1. Таха Хемди А. Введение в исследование операций, 7-е издание: пер. с англ. – М.: Издательский дом "Вильяме", 2005. – 912 с.

2. Грешилов А.А. Прикладные задачи математического программирования: учебное пособие. – 2-е изд. – М.: Логос, 2006. – 288 с.

3. Бережная Е. В. Математические методы моделирования экономических систем: учеб. пособие. – 2-е изд., перераб. и доп. / Е. В. Бережная, В. И. Бережной. – М.: Финансы и статистика, 2006. – 432 с.

4.

5.

6.