Результати роботи

Лабораторна робота №2

Excel: Використання критерію 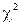для перевірки гіпотези про нормальний закон розподілу генеральної сукупності

Мета роботи – навчитись використовувати 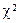критерій Пірсона для перевірки узгодження емпіричних та теоретичних розподілів статистичної величини за допомогою електронних таблиць Excel.

Задача. Задано інтервальний статистичний розподіл випадкової величини X – маса новонароджених дітей.

x_і	[1; 1,5]	(1,5; 2]	(2; 2,5]	(2,5; 3]	(3; 3,5]	(3,5; 4]	(4; 4,5]
n_i

Зробити припущення щодо закону розподілу генеральної сукупності та при рівні значущості α=0,01 перевірити цю гіпотезу.

Результати роботи

Для того, щоб висунути припущення щодо закону розподілу генеральної сукупності, перейдемо до дискретного статистичного розподілу (табл.1.):

Дискретний розподіл	Частота
1,25
1,75
2,25
2,75
3,25
3,75
4,25

Табл.1.

та побудуємо полігон частот (рис.1.):

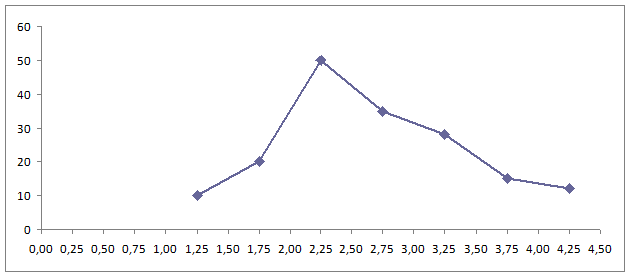
Рис.1.

Висуваємо гіпотезу

Н₀: маса новороджених дітей має нормальний закон розподілу.

Н_α: маса новороджених дітей має закон розподілу, відмінний від нормального.

Для обчислення теоретичних частот у випадку нормального закону розподілу знайдемо середнє вибіркове значення, дисперсію та середнє квадратичне відхилення (табл.2).

Обєм вибірки
Сер.значення	2,67
Дисперсія	0,61
Сер.кв.відхилення	0,78

Табл.2.

Обчислення спостережуваного значення статистичного критерію 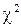подамо у вигляді таблиці 3:

x_i	x_i ₊₁	n_i	Ф(z_i)	Ф(z_i ₊₁)	nр_i	n_i – nр_i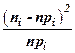
1,0	1,5		-0,48	-0,43		-1	0,111
1,5	2,0		-0,43	-0,31			0,182
2,0	2,5		-0,31	-0,09		-12	3,789
2,5	3,0		-0,09	0,16			1,488
3,0	3,5		0,16	0,36			0,758
3,5	4,0		0,36	0,46			0,235
4,0	4,5		0,46	0,49		-6	6,000

Табл.3.

Спостережуване значення критерію Пірсона 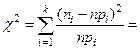12,564.

Критичнее значення критерію Пірсона 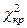= 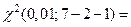13,277.

Висновок. Оскільки спостережуване значення критерію менше за критичне 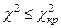, то приймаємо нульову гіпотезу про нормальний закон розподілу генеральної сукупності.