Домашнее задание ОТИ
Цель работы: записать результаты измерения по 50 точкам и представить его графически
Дано:
Вариант 4.Домашнее задание студенту __________________ по ОТИ.
1.Записать результат измерения длины стержня, мм:
| 48.25 | 48.30 | 48.30 | 48.55 | 48.35 |
| 48.35 | 48.40 | 48.45 | 48.35 | 48.40 |
| 48.40 | 48.40 | 48.25 | 48.40 | 48.55 |
| 48.40 | 48.45 | 48.30 | 48.40 | 48.35 |
| 48.45 | 48.45 | 48.30 | 48.25 | 48.50 |
| 48.50 | 48.35 | 48.35 | 48.50 | 48.40 |
| 48.40 | 48.55 | 48.40 | 48.30 | 48.50 |
| 48.45 | 48.35 | 48.35 | 48.35 | 48.55 |
| 48.50 | 48.40 | 48.35 | 48.55 | 48.30 |
| 48.45 | 48.50 | 48.45 | 48.30 | 48.50 |
Обработка результата ведётся в три этапа:
1. Обнаружение и исключение ошибок.
2. Проверка нормальности закона распределения вероятности результата измерения.
3. Вычисление доверительного интервала математического ожидания ε и построение карты процесса.
1. Обнаружение и исключение ошибок.
В системах при измерениях могут происходить сбои, отказы аппаратуры, скачки напряжения, ошибки в записях данных. Появляются ошибки, вероятность которых не так мала. Необходимо пользоваться правилом, с помощью которого можно отбросить сомнительные результаты.
Это правило 3σ: Если при многократном измерении одной и той же физической величины постоянного размера сомнительные значения результата измерения отличаются от среднего больше чем на 3σ, то с вероятностью больше 0,997 они являются ошибочными и их следует отбросить. σ – дисперсия.

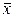 -3σ
-3σ 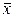 +3σ
+3σ
х 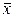 х
х
При расчётах принимать σ=s, так как среднее квадратичное отклонение является оценкой дисперсии. Ошибочными будут те значения, которые не входят в интервал:
[ 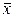 -3s;
-3s; 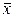 +3s].
+3s].
Для проведения анализа результатов измерений занесём вспомогательные расчёты в таблицу 2.
Таблица 2 – Вспомогательные расчёты
| xi | mi | mi· xi | xi- 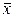
| (xi- 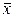 )2 )2
| (xi- 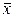 )2·mi )2·mi
|
| 48,25 | 144,75 | -0,153 | 0,023409 | 0,070227 | |
| 48,30 | 338,1 | -0,103 | 0,010609 | 0,074263 | |
| 48,35 | 483,5 | -0,053 | 0,002809 | 0,02809 | |
| 48,40 | 532,4 | -0,003 | 0,000016 | 0,000176 | |
| 48,45 | 339,15 | 0,047 | 0,002209 | 0,015463 | |
| 48,50 | 339,5 | 0,097 | 0,009409 | 0,065863 | |
| 48,55 | 242,75 | 0,147 | 0,021609 | 0,108045 | |
| Ʃ | 2420,15 | 0,07007 | 0,362127 |
mi – количество раз, которое xi повторяется в массиве
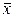 - среднее арифметическое результатов измерений.
- среднее арифметическое результатов измерений.
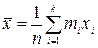 =
= 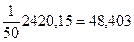 мм, (1)
мм, (1)
где k – кол-во интервалов.
Среднее квадратическое отклонение определяется по формуле:
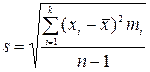 =
= 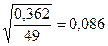 мм. (2)
мм. (2)
Найдём границы интервала [ 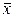 -3s;
-3s; 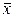 +3s].
+3s].
Все полученные значения входят в доверительный интервал [48,145; 48,661], следовательно, ошибочных значений нет.
Если какие-либо значения оказываются ошибочными, их отбрасывают, и проверка на ошибки проводится снова.
Если все значения попали в данный интервал, делаем вывод, что грубых ошибок нет и можно приступить к проверке на нормальность закона распределения.
2. Проверка нормальности закона распределения результата измерений
При обработке экспериментальных данных возникает вопрос, подчиняются результаты измерения нормальному закону. Не противоречивость такой гипотезы должна быть обязательно проверена, т.к. большинство классических методов математической статистики, используемых в задачах обработки измерений, могут быть применимы, только если распределение нормальное.
Для проверки гипотезы о нормальности построим по результатам экспериментальных данных гистограмму (рисунок 1). Для этого разбиваем наш массив на интервалы. При числе измерений 40-100 число интервалов 6-9.
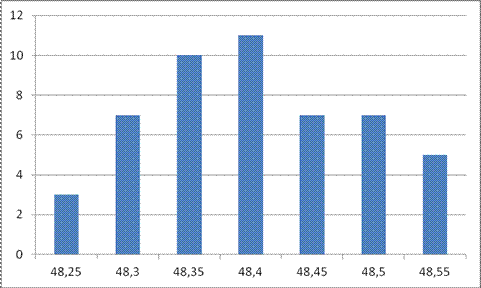 Рисунок 1 – Гистограмма результатов измерений
Рисунок 1 – Гистограмма результатов измерений
Математическая статистика даёт несколько показателей, по которым можно судить, насколько фактическое значение согласуется с нормальным распределением. Известны критерии Пирсона, Колмогорова, Смирнова и др.
В данном случае согласованность статистического и выбранного теоретического распределения проверим с помощью критерия Пирсона 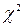 .
.
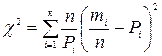 . (3)
. (3)
При использовании этого критерия за меру расхождения экспериментальных данных с теоретическими применяется сумма квадратов отклонений частности 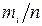 (вероятность появления i числа в этом интервале) от теоретической вероятности попадания отдельного результата измерения в i интервал. Причём каждое слагаемое берётся с коэффициентом
(вероятность появления i числа в этом интервале) от теоретической вероятности попадания отдельного результата измерения в i интервал. Причём каждое слагаемое берётся с коэффициентом 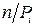 .
.
Если 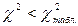 , то гипотеза о нормальном законе распределения вероятности результатов измерения принимается.
, то гипотеза о нормальном законе распределения вероятности результатов измерения принимается.
Расчёт значений частот теоретического ряда распределения для собранных данных представлен в таблице 3.
Таблица 3 – Расчёт значений частот теоретического ряда распределения для собранных данных
| i | Интервалы | mi | 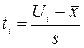
| Ф(ti) | 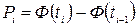
| 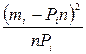
| |
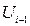
| 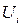
| ||||||
| - | - | - | - | -0,5 | - | - | |
| (-∞ | 48,275] | -1,4889412 | -0,4319 | 0,0681 | 0,04817181 | ||
| (48,275 | 48,325] | -0,9073236 | -0,3186 | 0,1133 | 0,31460282 | ||
| (48,325 | 48,375] | -0,3257059 | -0,1293 | 0,1893 | 0,03024036 | ||
| (48,375 | 48,425] | 0,25591177 | 0,1026 | 0,2319 | 0,03053256 | ||
| (48,425 | 48,475] | 0,83752944 | 0,2995 | 0,1969 | 0,82214576 | ||
| (48,475 | 48,525] | 1,41914711 | 0,4222 | 0,1227 | 0,12196007 | ||
| (48,525 | +∞) | 2,00076478 | 0,4772 | 0,055 | 1,84090909 | ||
| Σ | Итог | 1,79138242 | 3,20856246 |
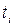 - показывает, на сколько стандартных отклонений s отстоит от среднего арифметического значения правая граница
- показывает, на сколько стандартных отклонений s отстоит от среднего арифметического значения правая граница 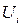 каждого интервала;
каждого интервала; 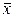 и s берём из предыдущего пункта.
и s берём из предыдущего пункта.
Ф(ti) – функции Лапласа. Значения берутся из статистической таблицы в зависимости от 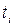 (приложение А). Причём, если
(приложение А). Причём, если 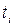 отрицательная, то и функция Лапласа берётся с минусом.
отрицательная, то и функция Лапласа берётся с минусом.
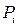 - теоретическая вероятность попадания в i интервал отдельного значения.
- теоретическая вероятность попадания в i интервал отдельного значения.
Суммирование чисел в последнем столбце даёт критерий Пирсона 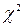 для нашего массива данных.
для нашего массива данных.
Сравнивая его с табличным 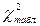 подтвердим или опровергнем гипотезу о нормальном распределении результатов измерения. В соответствии с таблицей критических значений критерия Пирсона (приложение Б) найдём табличное значение
подтвердим или опровергнем гипотезу о нормальном распределении результатов измерения. В соответствии с таблицей критических значений критерия Пирсона (приложение Б) найдём табличное значение 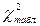 для уровня значимости α =0,05 и степени свободы r=k-3, где k - число интервалов.
для уровня значимости α =0,05 и степени свободы r=k-3, где k - число интервалов.
В данном примере 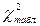 =9,49
=9,49
Фактическое значение 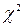 меньше табличного. Гипотезу о нормальном распределении принимаем. После это можно применить формулы для расчёта доверительного интервала.
меньше табличного. Гипотезу о нормальном распределении принимаем. После это можно применить формулы для расчёта доверительного интервала.
3. Вычисление доверительного интервала математического ожидания ε и построение карты процесса.
Результат измерений записывается в следующем виде:
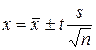 ; (4)
; (4)
где 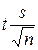 =- предельное отклонение,
=- предельное отклонение,
t – коэффициент Стьюдента, который зависит от доверительной вероятности (в нашем случае Р=0,95) и числа степеней свободы f=n-1 в нашем случае равен 2,0086 (приложение В).
Таким образом, результат измерений:
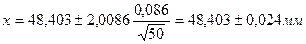 .
.
Контрольную карту процесса мы получаем подставив значения измерений (рисунок 2).
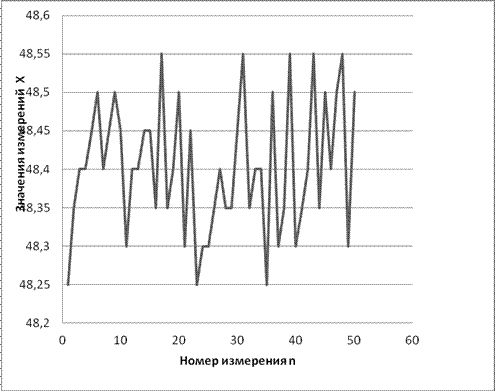
Рисунок 2 – Контрольная карта процесса измерений
 2015-10-13
2015-10-13 170
170






