Выборочное среднее 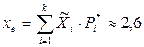 – несмещенная и состоятельная оценка математического ожидания.
– несмещенная и состоятельная оценка математического ожидания.
Исправленная выборочная дисперсия 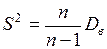 – несмещенная и состоятельная оценка дисперсии.
– несмещенная и состоятельная оценка дисперсии.
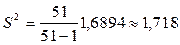
Выдвинута гипотеза о распределении генеральной совокупности Х по нормальному закону с плотностью 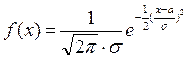 ,
, 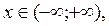 или
или 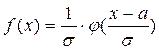 , где
, где 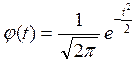
Найдем оценки параметров a и 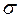 теоретического закона.
теоретического закона.
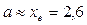 ,
,
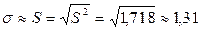 .
.
Заменяя a, 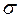 оценками, получаем теоретический закон распределения
оценками, получаем теоретический закон распределения
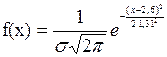 .
.
Так как для случайной величины, имеющей нормальное распределение, функцию плотности можно представить в виде 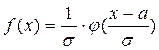 , где
, где 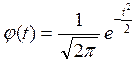 , то для нашего случая имеем:
, то для нашего случая имеем: 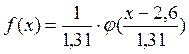 .
.
 2015-10-13
2015-10-13 247
247






