Алгоритм решения (метод северо- западного угла и метод потенциалов)

Транспортная задача по критерию стоимости

Постановка задачи

Пусть в р пунктах отправления находятся соответственно a₁, a₂, … a_p единиц однородного груза, который должен быть доставлен q потребителям в ко­личествах b₁, b₂, … b_q единиц. Заданы стоимости с_ik перевозок единицы груза из i-го пункта отправления k-му пункту потребления. Обозначим через х_ik ³ 0 (i =l, 2,..., р; k = 1, 2,..., q ) количество единиц груза, перевозимого из i-го склада k-му потребителю; тогда переменные x_ik должны удовлетворять следующим

ограничительным условиям:

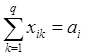(i =l, 2,..., р); 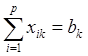(k = 1, 2,..., q); х_jk ³ 0.

Суммарные затраты на перевозки равны

L = c₁₁x₁₁ + c₁₂x₁₂ +…+ c_pqx_pq= .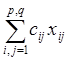

Следовательно, требуется найти pq переменных х_jk, удов­летворяющих указанным условиям и минимизирующих, целевую функцию L. Решение такой задачи разбивается на два этапа:

1) определение исходного опорного решения;

2) построение последовательных итераций, т. е. приближение к оптимальному решению.

Алгоритм решения (метод северо- западного угла и метод потенциалов)

1. Определение исходного опорного решения (метод северо- западного угла). Пусть мы имеем таблицу исход­ных данных задачи. Исходное опорное решение будем строить, по так называемому. правилу «северо-западного угла».

ai	bk	b1	b2	…	bk	…	bq
a1	x11	c11	x12	c12	…	x1k	c1k	…	x1q	c1q
a2	x21	c21	x22	c22	…	x2k	c2k	…	x2q	c2q
…	…	…	…	…	…	…
ai	xi1	ci1	xi2	ci2	…	xik	cik	…	xiq	ciq
…	…	…	…	…	…	…
ap	xp1	cp1	xp2	cp2	…	xpk	cpk	…	xpq	cpq

Заполним вышеуказанную таблицу, начиная с левого верхнего угла, двигаясь далее или по строке вправо, или по столбцу вниз. В клетку (1, 1) занесем меньшее из чисел a₁ и b₁, т.е. x₁₁ =min{ a₁, b₁ }.

Если a₁ > b₁ , то x₁₁ = b₁ и первый столбец «закрыт», т. е. потребности пер­вого потребителя удовлетворены полностью. Двигаемся далее по первой строке, записывая в соседнюю клетку (1, 2) меньшее из чисел a₁ - b₁ и b₂ т.е. x₁₂ =min{ a₁- b₁, b₂ }.

Если же b₂ > a₁, то аналогично «закрывается» первая строка и далее переходим к заполнению соседней клетки (2, 1), куда заносим x₂₁ =min{ а₂, b₁ - a₁ }.

Будем продолжать этот процесс до тех пор, пока на каком-то этапе не исчерпы­ваются ресурсы а_p и потребности b_q.

2. Построение последовательных итераций (метод потенциалов). Получив исходное опорное реше­ние, перейдем теперь к построению опорных решений, улучшающих друг друга: для этого применим метод потенциалов.

Итак, после построения исходного опорного решения все переменные разбиты на две группы: x_kl - базисные и x_pq - свободные; линейные функции стоимости перевозок выразятся через свободные переменные так:

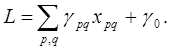
Для нахождения коэффициентов γ_рq при свободных переменных сопоставим каждому пункту отправления A_i некоторую величину u_i (i =l, 2,..., m), кото­рую назовем потенциалом пункта A_i, и каждому пункту назначения B_j величину v_j -потенциал пункта B_j. Свяжем эти величины равенством u_k + v_l = c_kl, где c_kl - стоимость перевозки одной тонны груза из пункта A_k в пункт B_l. Доказы­вается, что совокупность уравнений u_k + v_l = c_kl, составленных для всех базисных переменных, составляет совместную систему линейных уравнений, причем значе­ние одной из переменных можно задавать произвольно, и тогда значения осталь­ных переменных находятсяиз системы однозначно. Обозначим для свободных пе­ременных сумму соответствующих потенциалов через c'_pq, т. е. u_p + v_q = c'_pq и назовем её косвенной стоимостью (в отличие от данной стоимости c_pq ). Тогда коэффициенты при свободных переменных в соотношении (1) определяются с по­мощью равенства g_pq = c_pq - c'_pq.

Если все величины g_pq неотрицательны, то исходное решение является опти­мальным. Если же среди них имеются отрицательные, то переходим к следующе­му базису путем увеличения члена с отрицательным коэффициентом, оставляя другие переменные равными нулю.

Таким образом, правила вычислений по методу потенциалов сводятся к следующему.

1. Находят потенциалы u_k и v_l всех пунктов отправления A_k и назначе­ния B_l.

2. Выбирают какую-нибудь свободную переменную, для которой сумма по­тенциалов строго больше соответствующей стоимости, это соответствует элементу с отрицательным коэффициентом при свободной переменной в правой части функ­ции L.

3. Для выбранной в п. 2 переменной находят соответствующий ей цикл пересчета и производят сдвиг по этому циклу. Этот сдвиг приводит к новому допус­тимому решению.

4. Вышеуказанные операции 1—3 повторяют до тех пор, пока не получат оптимальный базис, т.е. неотрицательные коэффициенты при свободных перемен­ных в правой части линейной функции L.

Пример решения

Пример. В двух пунктах отправления А и В находится соответст­венно 150 и 90 т рекламной продукции. В пункты1, 2, 3 требуется доставить соответственно 60, 70 и 110 т. этой продукции. Стоимости перевозки тонны из пункта А в пункты 1, 2, 3 составляют соответственно 6, 10 и 4 руб., а из пункта В— 12, 2 и 8 руб. Составить оптималь­ный план перевозок продукции так, чтобы общая сумма транспорт­ных расходов была наименьшей.

Таблица 1.

ai	bk
А
В

Запишем исходные данные в табл. 1. Заполнение начнем с клетки (1, 1): x₁₁ = min {150, 60} = 60, первый столбец закрыт. Переходим к клетке (1, 2): x₁₂ = min {150—60, 70}= 70, второй столбец закрыт; далее, переходим к клетке (1, З):

x₁₃ = min {150—60—70, 110} = 20. Так как в третьем столбце оказался остаток, равный 90, то переходим к заполнению клетки (2, 3), куда заносим x₂₃ = min {90, 90} = 90. Поскольку остатки по строке и столбцу равны нулю, опорное исходное решение построено. Этому плану соответствуют затраты в количестве L =6^.60 +10^.70+4^.20+8^.90==1860 руб.

В правиле «северо-западного угла» не учитывается величина затрат c_ik, a потому исходное опорное решение часто может быть далеким от оптимального. Применяют также прием «минимального элемента», в котором учитывается вели­чина c_ik. В этом случае построение исходного опорного решения начинают с клет­ки с наименьшей величиной c_ik, в данном примере - с клетки (2, 2), где c₂₂ =2 (табл. 2). В эту клетку заносим x₂₂ = min { a₂, b₂ } = min {90, 70} =70.

Таблица 2

ai	bk
А
В
остаток

Остатки по строке и столбцу записываем в соответствующие клетки строки и столбца остатков. Столбец b₂ закрыт. Теперь переходим к клетке (1. 3), так как после c₂₂ = 2 наименьшим является c₁₃ =4. В клетку (1, 3) заносим x₁₃ =min{ a₁- b₁, b3 } = min { 150—60, 110}=90. Затем переходим к клетке (1, I):

x₁₁ =min{ a₁, b₁ } = min {150, 60}==60. Наконец, переходим к клетке (2, 3), в ко­торую заносим x₂₃ =min{ a₂- b₂, b₃ } = min {90—70, 110} =20.

Применяя это правило, мы получили другой вариант исходного опорного решения, при котором затраты L =6^.60+4^.90+2^.70+8^.20=1020 руб., т.е. сум­ма затрат ближе к оптимальному плану.

Воспользуемся изложенными общими понятиями и продолжим решение Примера. Мы получили исходное опорное решение (следуя правилу «минимального элемента»): x₁₁ = 60, x₁₂ = 0, x₁₃ =90, x₂₁ = 0, x₂₂ = 70, x₂₃ =20, L =1020. Для нахождения потенциалов необходимо решить систему

.

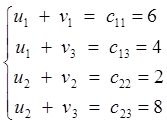Значение одного из неизвестных зададим произвольно, например u₁ =l. Тогда v₁ =5, v₃ = -3, u₂ =5, v₂ = -3. Далее вычисляем косвенные стоимости c'_pq:

c'₁₂ = u₁ + v₂ = -2, c'₂₁ = u₂ + v₁ = 10.

Подсчитаем теперь разности g_pq = c_pq - c'_pq:

g₁₂ = c₁₂ - c'₁₂ =10-(-2)=12, g₂₁ = c₂₁ - c'₂₁ = 12-10=2.

Следовательно, выражение L через свободные переменные имеет вид L = 1020 + 12 x₁₂ +2 x₂₁. Среди коэффициентов при переменных в правой части нет отрицательных. Значит, исходное опорное решение является оптимальным. Таким образом, правило «минимального элемента» сразу дает оптимальное решение.

Решим теперь эту же задачу при условии, что исходное решение получено по правилу «северо-западного угла», т.е. x₁₁ = 60, x₁₂ = 70, x₁₃ =20, x₂₃ =90, L =186O. Для нахождения потенциалов необходимо решить систему

.

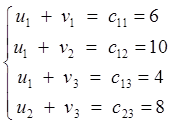Полагая u₁ =l, получим v₁ =5, v₂ = 9, v₃ = 3, u₂ = 5,.

Вычисляем косвенные стоимости c'_pq:

c'₂₁ = u₂ + v₁ = 10, c'₂₂ = u₂ + v₂ = 14.

Подсчитаем теперь разности g_pq = c_pq - c'_pq:

g₂₁ = c₂₁ - c'₂₁ =12-10= 2, g₂₂ = c₂₂ - c'₂₂ = 2-14= -12.

Следовательно, выражение L через свободные переменные имеет вид L = I860 + 2 x₂₁ - 12 x₂₂. Среди коэффициентов при переменных в правой части есть отрицательный при x₂₂, следовательно, можно попытаться уменьшить L, увеличив x₂₂ (сохранив нулевое значение x₂₁). Положим x₂₂ =l. Поскольку суммы значений неизвестных по строкам и столбцам должны остаться неизменными, нужно про­извести следующий балансовый пересчет:

	70 - l.	20+ l
l	90- l

Добавление l к x₂₂ компенсируется вычитанием l из x₁₂, а это в свою очередь ­прибавлением l к x₁₃ и т.д. до тех пор, пока мы не вернемся обратно к x₂₂. Обходя клетки по пунктирной ломаной линии, в однойиз вершин которой нахо­дится свободная переменная x₂₂ , а в остальных вершинах - базисные переменные (причем не обязательно все), мы получим так называемый цикл пересчета (лома­ная называется циклом), отвечающий свободной клетке x₂₂. Как видно из табли­цы, для неотрицательности переменных l можно увеличить до l =70, тогда получим второе опорное решение:

	0
0	70

т.е. x₁₁ = 60, x₁₂ = 0, x₁₃ =90, x₂₁ = 0, x₂₂ = 70, x₂₃ =20. Значение функции L для него составляет L =1860 – 12 ^, 70=1020, т. е. полу­чили оптимальное решение (судя по предыдущему решению).

Литература

1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М.”Высшая школа”. ч.1. -320 с.