Идеальный газ во внешнем потенциальном поле. Распределение Больцмана. Барометрическая формула

1. 4. Барометрическая формула.

При выводе основного уравнения молекулярно-кинетической теории предполагалось, что если на молекулы газа не действуют внешние силы, то молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул, с другой, приводят к некоторому стационарному состоянию газа, при котором концентрация молекул газа и его давление с высотой убывают. Выведем закон изменения давления газа с высотой, предполагая при этом, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте hравнор, то на высотеh+dhоно равно р +dp(рис.1.2). Приdh> 0,dр < 0, т.к. давление с высотой убывает. Разность давлений р и (р +dр) равна гидростатическому давлению столба газа авсd, заключенного в объеме цилиндра высотойdhи площадью с основанием равным единице. Это з апишется в следующем виде:p- (p+dp) =gρdh, -dp=gρdhилиdp= ‑gρdh, гдеρ– плотность газа на высотеh. Воспользуемся уравнением состояния идеального газа рV=mRT/Mи выразим плотностьρ=m/V=pM/RT. Подставим это выражение в формулу дляdр:

dp= -pMgdh/RTилиdp/p= -Mgdh/RT

Интегрирование данного уравнения дает следующий результат: Здесь С – константа и в данном случае удобно обозначить постоянную интегрирования черезlnC. Потенцируя полученное выражение, находим, что

При условии h=0 получим, что С=р₀, где р₀-давление на высотеh=0.

Д анное выражение называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты, или высоту, если известно давление.

Зависимость давления от высоты демонстрирует рисунок 1.3. Прибор для определения высоты над уровнем моря называется высотомером или альтиметром. Он представляет собой барометр, проградуированный в значениях высоты.

1. 5. Закон Больцмана о распределении частиц во внешнем потенциальном поле. @

Если воспользоваться выражением р = nkT, то можно привести барометрическую формулу к виду:

з 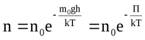десьn– концентрация молекул на высотеh,n₀– то же у поверхности Земли. Так как М =m₀N_A , гдеm₀ – масса одной молекулы, аR=kN_A, то мы получим П =m₀gh– это потенциальная энергия одной молекулы в поле тяготения. ПосколькуkT~‹ε_пост›, то концентрация молекул на определенной высоте зависит от соотношения П и ‹ε_пост›

Полученное выражение называется распределением Больцмана для внешнего потенциального поля. Из него следует, что при постоянной температуре плотность газа (с которой связана концентрация) больше там, где меньше потенциальная энергия его молекул.

1. 6. Распределение Максвелла молекул идеального газа по скоростям. @

При выводе основного уравнения молекулярно-кинетической теории отмечалось, что молекулы имеют различные скорости. В результате многократных соударений скорость каждой молекулы меняется со временем по модулю и по направлению. Из-за хаотичности теплового движения молекул все направления являются равновероятными, а средняя квадратичная скорость остается постоянной. Мы можем записать

П остоянство ‹υ_кв› объясняется тем, что в газе устанавливается стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Этот закон теоретически был выведен Д.К.Максвеллом. Он рассчитал функциюf(u), называемую функцией распределения молекул по скоростям. Если разбить диапазон всех возможных скоростей молекул на малые интервалы, равныеdu, то на каждый интервал скорости будет приходиться некоторое число молекулdN(u), имеющих скорость, заключенную в этом интервале (Рис.1.4.).

Функция f(v) определяет относительное число молекул, скорости которых лежат в интервале отu до u+ du. Это число - dN(u)/N= f(u)du.Применяя методы теории вероятностей, Максвелл нашел вид для функции f(u)

Д анное выражение - это закон о распределении молекул идеального газа по скоростям.Конкретный вид функции зависит от рода газа, массы его молекул и температуры (рис.1.5). Функция f(u)=0 при u=0 и достигает максимума при некотором значении u_в, а затем асимптотически стремится к нулю. Кривая несимметрична относительно максимума. Относительное число молекул dN(u)/N, скорости которых лежат в интервале du и равное f(u)du, находится как площадь заштрихованной полоски основанием dv и высотой f(u), показанной на рис.1.4. Вся площадь, ограниченная кривой f(u) и осью абсцисс равна единице, потому что, если просуммировать все доли молекул, имеющих всевозможные значения скорости, то получается единица. Как показано на рис.1.5, с ростом температуры кривая распределения смещается вправо, т.е. растет число быстрых молекул, но площадь под кривой остается постоянной, т.к. N = const.

Скорость u_в, при которой функция f(u) достигает максимума, называется наиболее вероятной скоростью. Из условия равенства нулю первой производной функцииf(v) ′ = 0 следует, что

Н 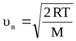а рисунке 1.4. отмечена еще одна характеристика – средняя арифметическая скорость молекулы. Она определяется по формуле:

Опыт, проведенный немецким физиком О.Штерном, экспериментально подтвердил справедливость распределения Максвелла (рисунок 1.5.). Прибор Штерна состоит из двух коаксиальных цилиндров. Вдоль оси внутреннего цилиндра со щелью проходит платиновая проволока, покрытая слоем серебра. Если пропустить по проволоке ток,она нагревается и серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра. Если прибор будет вращаться, то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние. Исследование количество осадка позволяет оценить распределение молекул по скоростям. Оказалось, что распределение соответствует максвелловскому.

Барометрическая формула. Распределение Больцмана

Основное уравнение молекулярно-кинетической теории связывает параметры состояния газа с характеристиками движения его молекул, т. е. устанавливает зависимость между давлением и объемом газа и кинетической энергией поступательного движения его молекул.

Для вывода уравнения рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически с одной и той же скоростью v, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку DS (рис. 1) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула массой т₀ передает стенке сосуда импульс m_ov - (- m_ov) = 2 m_ov.

Рис.1.

За время Dt площадки DS достигнут только те молекулы, которые заключены в объеме цилиндра с основанием DS и высотой v Dt. Число этих молекул равно п DS v Dt (n — число молекул в единице объема). Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент 'времени вдоль каждого из них движется 1/3 молекул, причем половина молекул движется вдоль данного направления в одну сторону, половина — в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку DS будет 1/6 п DS vDt.. При столкновении с площадкой эти молекулы передадут ей импульс P=2 m_ov 1/6 п DS vDt = 1/3 п m_ov ²DSDt

Тогда давление газа, оказываемое им на стенку сосуда,

р = F/DS=P/(DSDt)=1/3 п m_ov ² (1),

(так как F=dP/dt).

Если газ в объеме V содержит N молекул, движущихся с разными скоростями, то можно рассматривать среднюю квадратичную скорость, характеризующую всю совокупность молекул газа.

(2)

Уравнение (1) с учетом (2) примет вид

р = 1/3 п m_ov _кв² (3)

Учитывая, что п = N/V, получим рV = 1/3 N m_ov _кв²

или рV = 2/3 N (m_ov _кв²/2)= 2/3 E (4),

где Е — суммарная кинетическая энергия поступательного движения всех молекул газа.

Выражение (4) (т.е. рV = 2/3 E) или эквивалентное ему (3) называется основным уравнением молекулярно-кинетической теории идеальных газов. Точный расчет с учетом движения молекул по всевозможным направлениям дает ту же формулу.

Учитывая, что с одной стороны p = n kT, а с другой р = 1/3 п m_ov _кв², получим выражение для средней квадратичной скорости

(5),

так как молярная масса m = m₀N_A, где т₀ — масса одной молекулы, N_A — постоянная Авогадро, к = R/N_A. Отсюда легко найти, что при комнатной температуре молекулы кислорода имеют среднюю квадратичную скорость 480 м/с.

Средняя кинетическая энергия поступательного движения одной молекулы идеального газа, используя, что p = n kT, и р = 1/3 п m_ov _кв², равна

e = m_ov_кв ²/2 =3/2kT

Т.е. она пропорциональна термодинамической температуре и зависит только от нее. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа.

При выводе основного уравнения молекулярно-кинетической теории газов и максвелловского распределения молекул по скоростям предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул — с другой, приводят к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает.

Выведем закон изменения давления с высотой, предполагая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте h равно р, то на высоте h + dh оно равно р + dp (при dh> О dp < 0, так как давление с высотой убывает). Разность давлений р и р + dp равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью, равной единице площади:

р - (р + dp) = ρ gdh,

где ρ — плотность газа на высоте h. Следовательно,

dp =- ρ gdh. (1)

Воспользовавшись уравнением состояния идеального газа pV = m/mRT,где m -масса газа, m — молярная масса газа), находим, что плотность газа равна

r= m/V = pm/(RT).

Подставив в (1), получим

или

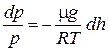
Проинтегрируем это уравнение с учетом того, что р — давление на высоте h, а давление на h =0 (на поверхности земли) равно p_o.

Получим

(2),

так как m = m₀N_A, и R = kN_A, где т_o — масса одной молекулы, N_A — постоянная Авогадро.

Выражение (2) называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты (или, измерив давление, найти высоту). Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяжелее газ.

Барометрическую формулу (2) можно преобразовать, если воспользоваться выражением р = пкТ:

(3)

Здесь n — концентрация частиц на высоте h, а n_o - концентрация частиц на высоте h =0.

Из формулы (3) следует, что с понижением температуры число молекул на определенной высоте h убывает. При T =0 все молекулы оказались бы на поверхности земли. Сила тяжести стремиться опустить молекулу на землю, а тепловое движение разбрасывает их по высотам, поэтому распределение молекул в атмосфере с высотой определяется балансом этих тенденций.

Если учесть, что m_ogh = П — потенциальная энергия молекулы в поле тяготения то формулу можно переписать.

(4)

Выражение (4) называется распределением Больцмана во внешнем потенциальном поле. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана (4) справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

БАРОМЕТРИЧЕСКАЯ ФОРМУЛА. РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА

Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести.

Для идеального газа, имеющего постоянную температуру и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения одинаково), барометрическая формула имеет следующий вид:

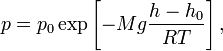
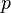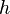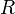где — давление газа в слое, расположенном на высоте , — давление на нулевом уровне (), — молярная масса газа, — универсальная газовая постоянная, — абсолютная температура. Из барометрической формулы следует, что концентрация молекул (или плотность газа) убывает с высотой по тому же закону:

где 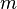— масса молекулы газа, — постоянная Больцмана.

Барометрическая формула может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см. Статистика Максвелла — Больцмана). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на этом, французский физик Ж. Перрен в 1908 году применил барометрическую формулу к распределению по высоте частичек эмульсии, что позволило ему непосредственно определить значение постоянной Больцмана.

Барометрическая формула показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина , определяющая быстроту спада плотности, представляет собой отношение потенциальной энергии частиц к их средней кинетической энергии, пропорциональной . Чем выше температура , тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести (при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести может изменяться за счёт двух величин: ускорения и массы частиц .

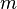Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.

Реальное распределение давления и плотности воздуха в земной атмосфере не следует барометрической формуле, так как в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.

Барометрическая формула лежит в основе барометрического нивелирования — метода определения разности высот между двумя точками по измеряемому в этих точках давлению ( и ). Поскольку атмосферное давление зависит от погоды, интервал времени между измерениями должен быть возможно меньшим, а пункты измерения располагаться не слишком далеко друг от друга. Барометрическая формула записывается в этом случае в виде: (в м), где — средняя температура слоя воздуха между точками измерения, — температурный коэффициент объёмного расширения воздуха. Погрешность при расчётах по этой формуле не превышает 0,1—0,5 % от измеряемой высоты. Более точна формула Лапласа, учитывающая влияние влажности воздуха и изменение ускорения свободного падения.

Распределение Больцмана

В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана:

n = n0exp(-mgh / kT)

где n - концентрация молекул на высоте h, n0 - концентрация молекул на начальном уровне h = 0, m - масса частиц, g - ускорение свободного падения, k - постоянная Больцмана, T - температура.

Барометрическая формула. Распределение Больцмана.

Основное уравнение молекулярно-кинœетической теории связывает параметры состояния газа с характеристиками движения его молекул, т. е. устанавливает зависимость между давлением и объёмом газа и кинœетической энергией поступательного движения его молекул.

Для вывода уравнения рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически с одной и той же скоростью v, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку DS (рис. 1) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула массой т₀ передает стенке сосуда импульс m_ov - (- m_ov) = 2 m_ov.

Рис.1.

За время Dt площадки DS достигнут только те молекулы, которые заключены в объёме цилиндра с основанием DS и высотой v Dt. Число этих молекул равно п DS v Dt (n — число молекул в единице объёма). Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент 'времени вдоль каждого из них движется 1/3 молекул, причем половина молекул движется вдоль данного направления в одну сторону, половина — в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку DS будет 1/6 п DS vDt.. При столкновении с площадкой эти молекулы передадут ей импульс P=2 m_ov 1/6 п DS vDt = 1/3 п m_ov ²DSDt

Тогда давление газа, оказываемое им на стенку сосуда,

р = F/DS=P/(DSDt)=1/3 п m_ov ² (1),

(так как F=dP/dt).

В случае если газ в объёме V содержит N молекул, движущихся с разными скоростями, то можно рассматривать среднюю квадратичную скорость, характеризующую всю совокупность молекул газа.

(2)

Уравнение (1) с учетом (2) примет вид

р = 1/3 п m_ov _кв² (3)

Учитывая, что п = N/V, получим рV = 1/3 N m_ov _кв²

или рV = 2/3 N (m_ov _кв²/2)= 2/3 E (4),

где Е — суммарная кинœетическая энергия поступательного движения всœех молекул газа.

Выражение (4) (ᴛ.ᴇ. рV = 2/3 E) или эквивалентное ему (3) принято называть основным уравнением молекулярно-кинœетической теории идеальных газов. Точный расчет с учетом движения молекул по всœевозможным направлениям дает ту же формулу.

Учитывая, что с одной стороны p = n kT, а с другой р = 1/3 п m_ov _кв², получим выражение для средней квадратичной скорости

(5),

так как молярная масса m = m₀N_A, где т₀ — масса одной молекулы, N_A — постоянная Авогадро, к = R/N_A. Отсюда легко найти, что при комнатной температуре молекулы кислорода имеют среднюю квадратичную скорость 480 м/с.

Средняя кинœетическая энергия поступательного движения одной молекулы идеального газа, используя, что p = n kT, и р = 1/3 п m_ov _кв², равна

e = m_ov_кв ²/2 =3/2kT

Т.е. она пропорциональна термодинамической температуре и зависит только от нее. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, термодинамическая температура является мерой средней кинœетической энергии поступательного движения молекул идеального газа.

При выводе основного уравнения молекулярно-кинœетической теории газов и максвелловскогораспределœения молекул по скоростям предполагалось, что на молекулы газа внешние силы не действуют, в связи с этим молекулы равномерно распределœены по объёму. При этом молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул — с другой, приводят к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает.

Выведем закон изменения давления с высотой, предполагая, что поле тяготения однородно, температура постоянна и масса всœех молекул одинакова. В случае если атмосферное давление на высоте h равно р, то на высоте h + dh оно равно р + dp (при dh> О dp < 0, так как давление с высотой убывает). Разность давлений р и р + dp равна весу газа, заключенного в объёме цилиндра высотой dh с основанием площадью, равной единице площади:

р - (р + dp) = ρ gdh,

где ρ — плотность газа на высоте h. Следовательно,

dp =- ρ gdh. (1)

Воспользовавшись уравнением состояния идеального газа pV = m/mRT,где m -масса газа, m — молярная масса газа), находим, что плотность газа равна

r= m/V = pm/(RT).

Подставив в (1), получим

или

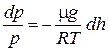
Проинтегрируем это уравнение с учетом того, что р — давление на высоте h, а давление на h =0 (на поверхности земли) равно p_o.

Получим

(2),

так как m = m₀N_A, и R = kN_A, где т_o — масса одной молекулы, N_A — постоянная Авогадро.

Выражение (2) принято называть барометрической формулой. Она позволяет найти атмосферное давление исходя из высоты (или, измерив давление, найти высоту). Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяжелœее газ.

Барометрическую формулу (2) можно преобразовать, в случае если воспользоваться выражением р = пкТ:

(3)

Здесь n — концентрация частиц на высоте h, а n_o - концентрация частиц на высоте h =0.

Из формулы (3) следует, что с понижением температуры число молекул на определœенной высоте h убывает. При T =0 всœе молекулы оказались бы на поверхности земли. Сила тяжести стремиться опустить молекулу на землю, а тепловое движение разбрасывает их по высотам, в связи с этим распределœение молекул в атмосфере с высотой определяется балансом этих тенденций.

В случае если учесть, что m_ogh = П — потенциальная энергия молекулы в поле тяготения то формулу можно переписать.

(4)

Выражение (4) принято называть распределœением Больцмана во внешнем потенциальном поле. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

В случае если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределœение Больцмана (4) справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

Распределение Больцмана

 

Распределение Больцмана определяет распределение частиц в силовом поле в условиях теплового равновесия. Больцман Людвиг (1844–1906) – австрийский физик-теоретик, один из основоположников классической статистической физики. Основные работы – в области кинетической теории газов, термодинамики и теории излучения. Вывел основное кинетическое уравнение газов, являющееся основой физической кинетики. Впервые применил к излучению принципы термодинамики.

Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения P = nkT, падает.

Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов.

Исходя из основного уравнения молекулярно-кинетической теории: P = nkT, заменим P и P₀ в барометрической формуле (2.4.1) на n и n₀ и получим распределение Больцмана для молярной массы газа:

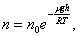(2.5.1)

где n₀ и n - число молекул в единичном объёме на высоте h = 0 и h.

Так как а , то (2.5.1) можно представить в виде

(2.5.2)

С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При T = 0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh – это потенциальная энергия U, то на разных высотах U = mgh – различна. Следовательно, (2.5.2) характеризует распределение частиц по значениям потенциальной энергии:

,

(2.5.3)

– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n₀ – число молекул в единице объёма там, где U = 0.

На рисунке 2.11 показана зависимость концентрации различных газов от высоты. Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.

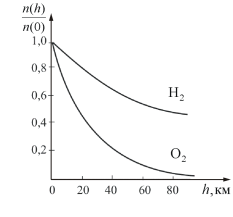
Рис. 2.11

Из (2.5.3) можно получить, что отношение концентраций молекул в точках с U₁ и i>U₂ равно:

.

(2.5.4)

Больцман доказал, что соотношение (2.5.3) справедливо не только в потенциальном поле сил гравитации, но и в любом потенциальном поле, для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения.