2017-11-01
499Поток минимальной стоимости. Предположим, что задана сеть с пропускными способностями дуг cij. Пусть также для каждой дуги (i; j) заданы число sij, интерпретируемое как затраты (например, затраты на перевозку единицы груза из вершины i в вершину j). Задача поиска потока минимальной стоимости заключается в нахождении для заданной величины (р суммарного потока ее распределения по дугам, минимизирующего сумму затрат.
Частным случаем задачи о потоке минимальной стоимости является транспортная задача, в которой имеется двудольный граф (двудольным называется граф, множество вершин которого может быть разбито на два непересекающихся подмножества, причем ребра (дуги) графа соединяют вершины только из разных подмножеств), представленный на рисунке 4: вершины сети разбиты на две группы - m поставщиков и n потребителей.
Известно, что граф является двудольным тогда и только тогда, когда он не содержит циклов нечетной длины, или когда в нем все простые циклы имеют четную длину {теорема Кенига).
Для поставщиков заданы имеющиеся у них количества единиц
товара (груза и т.д.) a i 
, для потребителей - требуемые им
количества единиц товара bi, 
. Также известны затраты sij перевозки единицы товара от i -го поставщика j -му потребителю.
Пусть задача является замкнутой, то есть 
- суммарное предложение равно суммарному спросу (вводя фиктивного поставщика или фиктивного потребителя любую незамкнутую задачу можно свести к замкнутой). Требуется определить потоки товаров от потребителей к поставщикам, минимизирующие суммарные затраты.
Поставщики Потребители
s11
. s1j. b1
..
ai sij bj
. sin.
am..
. smj.
bn
smn
рис.4 Транспортная задача
Формально транспортную задачу можно записать в виде:
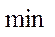
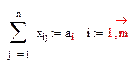
Добавляя к двудольному графу вход «0» и выход «z» и соединяя вход и выход с остальными вершинами дугами с потоком
x0i=ai, ,xjz=bj, 
, получаем задачу о потоке минимальной стоимости.
