Метод гребневой регрессии

ЛАБОРАТОРНААЯ РАБОТА

Исследование методов преобразования сигнала

По дисциплине «Преобразование Измерительных сигналов»

 

                                                                         

 

                                                                        Выполнила студентка

                                                                                              Факультета Кибернетики

                                                                                              Группы КС-61-09

                                                                                              Костылева Татьяна

 

 

Москва 2012-05-25

 

Цель работы:

Определить оптимальный метод преобразования сигнала из пяти предложенных. Продемонстрировать результаты всех измерений.

 

Теория по данной теме:

Первый метод, который мы рассмотрим-метод наименьших квадратов (МНК)

Метод наименьших квадратов — один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.

Метод наименьших квадратов применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина прямой или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятности; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

Большие затруднения представляются при определении из наблюдений величин, которые не могут быть измерены непосредственно. Если, например, желают определить элементы орбиты планеты или кометы, то светила эти наблюдаются несколько раз, и в результате получают лишь координаты их (склонение и прямое восхождение) в известные времена; самые же элементы выводятся затем решением уравнений, связывающих наблюдаемые координаты с элементами орбиты планеты или кометы. При этом, если бы число уравнений равнялось числу неизвестных, то для каждой неизвестной получилась бы одна определенная величина; если же число уравнений больше числа неизвестных, то, вследствие ошибок наблюдений, результаты решений отдельных групп этих уравнений в различных сочетаниях оказываются не совсем согласными между собой.Классический метод наименьших квадратов в ряде случаев, как известно, является не устойчивым, что приводит к большим погрешностям при обработке сигнала. Поэтому кроме классического метода МНК используют и его модификации. На пример:

-метод стандартизации;

-метод QR разложения;

Точность решения зависит от:

1. Вида функции.

2. Вида весовой функции

3. Уровня шума

 

Метод гребневой регрессии

В методе гребневой регрессия оптимальное значение коэффициента регуляризации определяется из условия плавности графиков зависимости компонент вектора решения от величины коэффициента регуляризации.

Сравнение полученного решения с точным значением возможно только в модельном эксперименте. В натуральном эксперименте этого сделать нельзя, так как неизвестно точное решение.

По этому выбрать оптимальное значение коэффициента регуляризации в этом методе не представляется возможным. Для выбора оптимального значения необходима дополнительная информация.

Если система уравнений очень плохо обусловлена или вырождена, то рассмотренные выше методы не дадут положительного результата. В этом случае целесообразно попытаться исправить матрицу системы уравнений таким образом чтобы она стала не вырожденной.

    Рассмотрим систему уравнений

                                  ,

где - действительная, симметричная, неотрицательно определенная матрица. Собственные числа такой матрицы попарно различны. Определитель матрицы  равен . Если l_n=0, то матрица будет вырождена.

    Рассмотрим матрицу , где r>0. Спектр собственных чисел этой матрицы имеет вид , а определитель равен                                                           

                                   ,

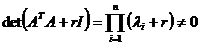т.е. матрица  не вырождена. Следовательно, система уравнений

                                          

имеет решение. Если r <<1, то можно ожидать, что решение исправленного уравнения будет мало отличатся от исходного уравнения. Определенные трудности при реализации данного метода связаны с отсутствием объективного метода определения оптимального значения коэффициента r. В методе гребневой регрессии его значение предлагается определять по графику зависимостей , выбирая в качестве оптимального значения r0 то минимальное значение r начиная с которого  начинают слабо изменяться. Очевидно, что данная методика весьма субъективна и будет давать положительный результат далеко не всегда. Для получения более точных результатов необходимо иметь объективную методику определения оптимального значения коэффициента r.    

Метод Тихонова

 Регуляризация Тихонова (в английской литературе ridge regression) для интегральных уравнений позволяет балансировать между соответствием данным и маленькой нормой решения. L2 = Σ(yt-y)2 + λ*Σ(ai)2

                ,

известно[1], что это уравнение является некорректным по Адамару, т.е. погрешность решения этого уравнения, даже при малых погрешностях y(t), может быть очень большой.

Для решения подобных задач применяется метод регуляризации Тихонова, а сами задачи называются корректными по Тихонову. Положим, что y(t) содержит случайную погрешность x(t). Тогда каждой реализации случайной погрешности x(t) будет соответствовать свое решение интегрального уравнения, очевидно, что среди этих решений есть и такие которые имеют малую погрешность. Для того чтобы из этого множества решений выбрать те которые устраивают нас по точности необходимо использовать какую либо дополнительную информацию и виде решения.

    Поскольку при численном решении интегрального уравнения оно заменяется системой линейных уравнений, то дальнейшие выкладки будут приведены для случая системы линейных уравнений.

    Представим интегральное уравнение в виде

                                    

где

                              

                         x(t) - случайная функция (погрешность измерения).

    Положим, что известна погрешность измерения вектора  (например по результатам тестирования установки) т.е. известно значение величины

                                  

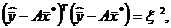
где х^*- точное решение уравнения.

    Обозначим через d квадрат невязки решения, равный

                                      

и будем искать решение уравнения, имеющее минимальную норму при условии, что квадрат невязки решения равно x². Следовательно, решение исходной задачи сведено к решению вариационной задачи на условный экстремум, которая может быть решена методом неопределенных множителей Лагранжа.

Фильтр Калмана

Фильтр Калмана это эффективный рекурсивный фильтр, который оценивает состояние линейной динамической системы по серии неточных измерений. Он используется в широком спектре задач от радаров до систем технического зрения, и является важной частью теории систем.

Фильтры Калмана основываются на линейных динамических системах, дискретизированных по времени. Они моделируются цепями Маркова, построенными на линейных операторах с внесенными погрешностями с нормальным Гауссовым распределением. Состояние системы считается вектор из действительных чисел. При каждом шаге по времени, линейный оператор применяется к вектору состояния системы, добавляется некоторая погрешность и опционально некоторая информация об управляющих воздействиях на систему, если таковая известна. После чего другим линейным оператором с другой погрешностью добавляется видимая информация о состоянии системы. Фильтр Калмана можно рассматривать в качестве аналога скрытым моделям Маркова, с тем ключевым отличием, что переменные, описывающие состояние системы, являются элементами бесконечного множества действительных чисел (в отличие от конечного множества пространства состояний в скрытых моделях Маркова). Кроме того, скрытые модели Маркова могут работать с произвольными распределениями для следующих значений переменных состояния системы, в отличие от модели стандартного Гауссового распределения, поддерживаемого фильтрами Калмана.

Фильтр Калмана является разновидностью рекурсивного фильтра. Это означает, что только результат предыдущей итерации фильтра (в виде оценки состояния системы и оценки погрешности определения этого состояния) и текущие наблюдения нужны для расчета текущего состояния системы. В отличие от пакетных фильтров не требуется хранение никакой истории наблюдений. В следующем дальше тексте запись 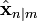означает оценку состояния системы в момент времени n при учете наблюдений (измерений) с начала работы фильтра и по момент времени m включительно.

 

 

Состояние фильтра содержится в двух переменных:

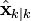• , оценочное состояние системы в момент времени k, которое получено на основании начального состояния системы и всех наблюдений по момент времени k включительно;
• , матрица ковариаций этого состояния, включающая в себя оценку дисперсий погрешности вычисленного состояния и уровни ковариаций, показывающих выявленные взаимосвязи между параметрами состояния системы.

Итерация фильтра Калмана делится на две фазы: Предсказание и Учет наблюдений. Фаза предсказания использует вычисленное на предыдущем шаге состояние для получения через модель системы оценочного состояния на текущем шаге. В фазе учета наблюдения информация об измерениях произведенных на текущем шаге используется для уточнения информации о состоянии системы, что делает её в результате (надеемся) более точной.

Практическая часть:

МНК

Выберем 1 функцию и 1 весовую. Шум не добавляем. Изучим полученный результат.

Из всех полученных результатов только один метод МНК- QR-разложение дал правильный результат. Остальные варианты даже близко не подходят к решению. Рассмотрим 2 функцию.

Как видно из графиков 2 функции, не сработал ни один из методов МНК. QR-разложение лишь в конце стало приближаться к норме. Даже несмотря на низкий уровень шума, решение методом МНК не приближается к истинному.

Если мы увеличим уровень шума, то решение абсолютно расходится.

Вывод: МНК крайне неточный метод, в редких случаях лишь QR-разложение дает положительный результат. В общем случае точность данного метода зависит от вида самой функции, а также весовой, и уровня шума.

Метод гребневой регрессии:

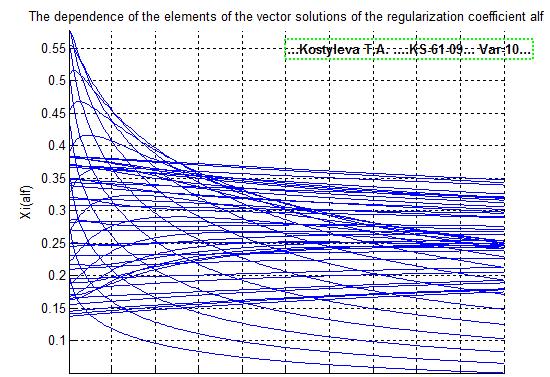
В данном методе нам предлагается самим выбрать коэффициент регуляризации. Сначала возьмем данный, который равен 0.1. Решение при этом не получилось

Попробуем менять коэффициент и понаблюдаем, как будет меняться результат.

Уменьшив коэффициент регуляризации решение стало стремиться к оптимальному. Попробуем увеличить ещё

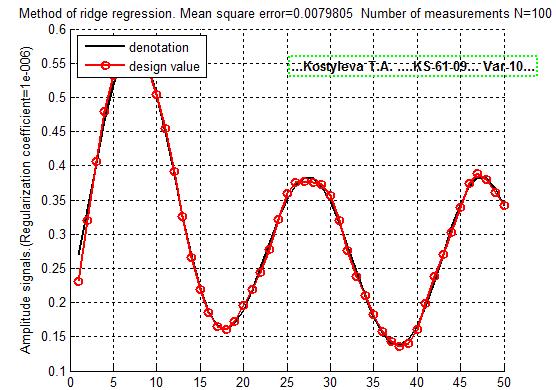
Увеличив К до 0.000001 мы почти в плотную подобрались к точному решению.

Но когда значение коэффициента регуляризации достигло 0.00000001, решение снова стало «отдаляться»

Используя третью весовую функцию нам сразу же удалось найти решение и подходящий коэффициент регуляризации, он равен 0.01

Вывод: Точность решения методом гребневой регрессии зависит от коэффициента регуляризации. Важно найти оптимальное значение, чтобы попасть именно в нужное решение.

Метод Тихонова

При очень низком уровне шума, решение методом Тихонова получилось довольно точным. Возьмем 2 весовую функцию, и немного увеличим шум.

После увеличения уровня шума-решение заметно ухудшилось.

Сильно уменьшив уровень шума в 3 весовой функции, мы получили достаточно неплохой результат, хоть и не совсем точный.

Вывод: Точность решения зависит как от уровня шума правой части, так и от вида весовой функции. Метод Тихонова сильно сглаживает решение. Главный недостаток-погрешность растет с увеличением количества измерений из-за постоянных округлений.

Итеративный МНК

Как и классический МНК, итеративный не дает нам точного решения.

Увеличив число итераций и немного уменьшив шум, мы получаем вполне приличный результат. ИМНК не полностью справился с задачей, но увеличив число итераций ещё на пару порядков, результат будет точнее.

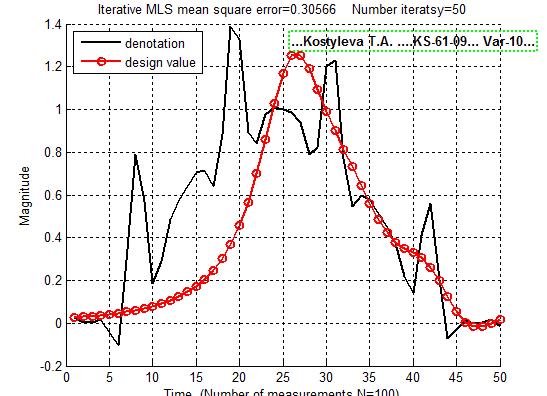
А вот со 2 функцией итеративный МНК дал очень плохой результат, хотя уровень шума был достаточно низким.

Увеличив число итераций до 1000, решение стало больше напоминать верное, но оно по прежнему далеко от идеала.

Но сделав число итераций очень большим (около 3000), решение снова уходит от нас. Это происходит из-за накопленных ошибок.

Вывод: Метод ИМНК гораздо точнее классического МНК, но из-за накапливания погрешностей его также нельзя назвать точным.

Фильтр Калмана:

Следуя указанным значениям в примере, мы не можем судить о правильности метода из-за недостаточного числа итераций. Увеличим их

Приняв 1000 за количество итераций, наше решение становиться практически точным.

А уже на 2 весовой, метод фильтра Калмана не сработал даже при большом числе итераций.

Во 2 функции и в 3 весовой мы получаем довольно неплохой результат, учитывая средний уровень шума и небольшое число итераций.

Вывод: Метод Калмана является довольно точным. Его точность зависит от начального приближения и от количества итераций и уровня шума.

Общий вывод:

Выполнив данную лабораторную работу, можно с уверенностью сказать что МНК является самым неочным, в метод фильтра Калмана, наоборот. Даже при высоком уровне шума и и среднем числе итераций, мы получаем вполне приемлимые данные.

 

[1]