Задачи для самостоятельного решения

Системы линейных уравнений.

Пусть дана система n линейных уравнений с n неизвестными:

Решением системы называется совокупность n чисел 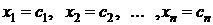, при подстановке которых в систему получаются верные числовые равенства.

Решить систему – значит найти все её решения или доказать, что их нет.

Система, имеющая хотя бы одно решение, называется совместной; а система, не имеющая ни одного решения – несовместной.

Матрица А, составленная из коэффициентов , называется матрицей системы и имеет вид .

Матричный способ решения СЛУ.

Свободные члены  и неизвестные  можно записать в виде матриц-столбцов:

.

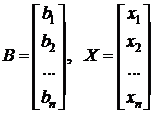Тогда систему уравнений можно записать в виде:

 или АХ=В.

Следовательно,

Пример 1. Решить матричным способом систему линейных уравнений:

Решение. .

----------------------------------------------------------------------------------------------------------------

Системы линейных уравнений. Стр.1

Следовательно, .

Тогда .

Ответ:

Формулы Крамера.

Если 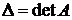 – определитель матрицы системы – не равен нулю, то система имеет единственное решение, которое можно найти по формулам Крамера:

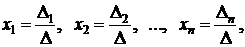
где  – определители, получаемые из  путём замены j – того столбца на столбец свободных членов.

Пример 2. Решить с помощью формул Крамера систему линейных уравнений:

Решение.

  (см. пример 1);

;

; .

Значит,

----------------------------------------------------------------------------------------------------------------

Системы линейных уравнений. Стр.2

Метод Гаусса.

Метод Гаусса (метод последовательного исключения переменных) состоит в следующем.

1. Систему уравнений приводят к эквивалентной ей системе (множество их решений совпадает) с треугольной матрицей. Эти действия называют прямым ходом.

2. Из полученной треугольной системы переменные находят с помощью последовательных подстановок, начиная с последних. Эти действия называют обратным ходом.

При выполнении прямого хода используются следующие преобразования:

1. Умножение и деление коэффициентов и свободных членов на одно и то же число.

2. Сложение и вычитание уравнений.

3. Перестановка уравнений системы.

4. Исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободный член равны нулю.

Пример 3. Решить методом Гаусса систему линейных уравнений:

Решение. Составим расширенную матрицу системы и приведём её к треугольному виду.

Составим систему уравнений, соответствующую последней полученной матрице:

Решим полученные уравнения, начиная с последнего:

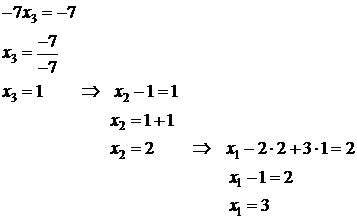
Ответ:

----------------------------------------------------------------------------------------------------------------

Системы линейных уравнений. Стр.3

Задачи для самостоятельного решения.

№1. Решить систему линейных уравнений:

а) матричным способом; б) по формулам Крамера; в) методом Гаусса.

№2. Решить систему линейных уравнений методом Гаусса:

а) ; б) .

 

Домашнее задание.

№1. Решить систему линейных уравнений:

а) матричным способом; б) по формулам Крамера; в) методом Гаусса.

№2. Решить систему линейных уравнений методом Гаусса:

----------------------------------------------------------------------------------------------------------------

Системы линейных уравнений. Стр.4