Біо-Савара-Лапласа закон - закон, що визначає величину напруженості магнітного поля, створюваного електричним струмом. Величина напруженості магн. поля  в точці М, створеної струмом І, що тече по елементу
в точці М, створеної струмом І, що тече по елементу
Лаплас узагальнив результати експериментів Біо і Савара у вигляді диференціального закону, який називається законом Біо - Савара - Лапласа:
 ,де
,де  – вектор, що числово дорівнює довжині
– вектор, що числово дорівнює довжині  елемента провідника і збігається за напрямком з напрямком електричного струму,
елемента провідника і збігається за напрямком з напрямком електричного струму, 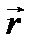 – радіус-вектор, проведений від елемента провідника
– радіус-вектор, проведений від елемента провідника  до точки поля А, що розглядається (рис. 162),
до точки поля А, що розглядається (рис. 162),  – магнітна стала
– магнітна стала
У векторній формі цей закон має вигляд  , де
, де 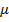 - відносна магнітна проникність середовища, безрозмірна величина;
- відносна магнітна проникність середовища, безрозмірна величина; 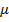 о – магнітна постійна (
о – магнітна постійна (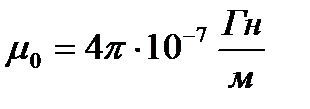 ); I – струм у провіднику;
); I – струм у провіднику;  - елемент провідника;
- елемент провідника;  - відстань від елемента струму до точки, в якій знаходиться індукція магнітного поля
- відстань від елемента струму до точки, в якій знаходиться індукція магнітного поля 
Закон Біо – Савара - Лапласа для напруженості магнітного поля Н має вигляд 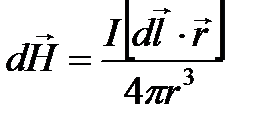 ,або в скалярній формі
,або в скалярній формі  . [ або з конспекта -
. [ або з конспекта -  ]
]

18 Магнітна індукція нескінченно довгого провідника зі струмом, кругового провідника зі струмом.
- Поле прямого лінійного провідника з струмом.
Обчислимо індукцію магнітного поля в точці А, розміщеній а відстані  від нескінчено довгого лінійного провідника з струмом І (рис. 1).
від нескінчено довгого лінійного провідника з струмом І (рис. 1).
 Для цього поділимо провідник на нескінченно малі елементи dl і запишемо закон Біо-Савара-Лапласа:
Для цього поділимо провідник на нескінченно малі елементи dl і запишемо закон Біо-Савара-Лапласа:  . Враховуючи, що для заданого напрямку струму I всі елементарні значення індукції магнітного поля в точці А направлені в один бік по прямій, перпендикулярній до площини рисунка, результуюча індукція магнітного поля рівна:
. Враховуючи, що для заданого напрямку струму I всі елементарні значення індукції магнітного поля в точці А направлені в один бік по прямій, перпендикулярній до площини рисунка, результуюча індукція магнітного поля рівна:  . (1)
. (1)
В цьому виразі три змінних (rdl) до однієї змінної. З рис.1 маємо:
 ;
; 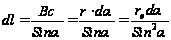 . Підставимо значення
. Підставимо значення  і
і  у формулу (1)
у формулу (1)  , Отже
, Отже  , а
, а
після інтегрування  (2) Для провідника скінченої довжини індукція магнітного поля залежить від
(2) Для провідника скінченої довжини індукція магнітного поля залежить від  і
і  (рис.2). Для нескінченного провідника із струмом
(рис.2). Для нескінченного провідника із струмом  , тому
, тому 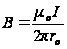 (3)
(3)  Таким чином: індукція магнітного поля нескінченно довгого лінійного провідника із струмом прямопропорційна силі струму і обернено пропорційна відстані
Таким чином: індукція магнітного поля нескінченно довгого лінійного провідника із струмом прямопропорційна силі струму і обернено пропорційна відстані  точки від провідника.
точки від провідника.
- Поле в центрі лінійного колового провідника радіуса
 по якому проходить струм силою І.
по якому проходить струм силою І.
В цьому випадку (рис.3) елементарні значення індукції 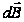 , кожного елемента
, кожного елемента  в точці 0 будуть направлені в один бік (від нас за площину рисунку) тоді
в точці 0 будуть направлені в один бік (від нас за площину рисунку) тоді 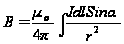 .
.
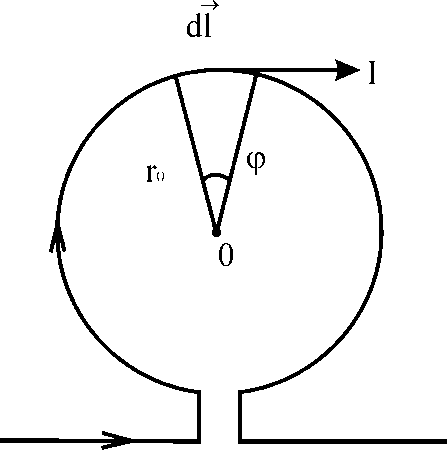 Для довільного елемента dl колового провідника
Для довільного елемента dl колового провідника  ;
;  ;
;  . Тоді
. Тоді  .
.
Отже  (4)
(4)
Отже: індукція магнітного поля колового провідника прямопропорційна силі струму і оберненопропорційна радіусові провідника.
Якщо коловий провідник має N витків і котушка плоска, то  (5) або
(5) або  ;
;
NI - величина, що дорівнює добутку кількості витків катушки на силу струму в них називається числом ампервитків.
Закон Ампера
Закон Ампера — закон взаємодії постійних струмів Із закону Ампера виходить, що паралельні провідники з постійним струмом, поточними в одному напрямі, притягуються, а в протилежному — відштовхуються. Законом Ампера називається також закон, що визначає силу, з якою магнітне поле діє на малий відрізок провідника із струмом.
 Сила
Сила  , с которой магнитное поле действует на элемент
, с которой магнитное поле действует на элемент  проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины
проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины  проводника на магнитную индукцию
проводника на магнитную индукцию 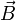 :
:  .
.
Правило лівої руки: Якщо ліву руку розташувати так, щоб 4 пальці вказували напрям струму, а лінії магнітної індукції входили в долню, то відхилений великий палець покаже напрям дії сили Ампера.
Сила Лоренца.
Сила Лоренца - сила, що діє на електричний заряд, який перебуває у електромагнітному полі.
 .Тут
.Тут  - сила, q - величина заряду,
- сила, q - величина заряду,  - напруженість електричного поля,
- напруженість електричного поля,  - швидкість руху заряду,
- швидкість руху заряду,  - вектор магнітної індукції.
- вектор магнітної індукції.
Якщо елемент  містить dN вільних носіїв заряду, то сила
містить dN вільних носіїв заряду, то сила 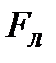 , що припадає на один електрон, дорівнює:
, що припадає на один електрон, дорівнює:  , де
, де 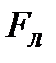 – сила Лоренца.
– сила Лоренца.
Кількість носіїв заряду dN в елементі провідника  запишемо через їх концентрацію n та об’єм dV елемента: dN=ndV=nS
запишемо через їх концентрацію n та об’єм dV елемента: dN=ndV=nS  , S – площа поперечного перерізу провідника. Тоді
, S – площа поперечного перерізу провідника. Тоді  .
.
Оскільки за електронною теорією  , то
, то  , або
, або 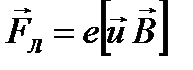 , де
, де 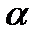 – кут між векторами
– кут між векторами  і
і  . В загальному випадку
. В загальному випадку  .
.
Якщо на рухомий електричний заряд, крім магнітного поля з індукцією  , діє і електричне поле з напруженістю
, діє і електричне поле з напруженістю  , то результуюча сила
, то результуюча сила  , яка прикладена до заряду:
, яка прикладена до заряду:  . -- Це формула Лоренца.
. -- Це формула Лоренца.
Електричне поле діє на заряд із силою, направленою вздовж силових ліній поля. Магнітне поле діє лише на рухомі заряди. Сила дії магнітного поля перпендикулярна до силових ліній поля й до швидкості руху заряду.
Ефект Хола.
Ефект Холла - явище, при якому виникає поперечна різниця потенціалів під час розміщення провідника з постійним струмом в магнітному полі.  , де
, де 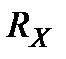 - коефіцієнт пропорційності і названий сталою Холла. А явище, яке експериментально виявив Холл, дістало назву ефект Холла.
- коефіцієнт пропорційності і названий сталою Холла. А явище, яке експериментально виявив Холл, дістало назву ефект Холла.
Явище ефекту Холла полягає в тому, що в провіднику з струмом, розміщеному в зовнішньому магнітному полі виникає електричне поле, напруженість якого перпендикулярна площині, в якій лежать вектори густини струму і індукції магнітного поля
Ефект Холла – це фізичне явище, яке полягає в наступному. Розглянемо пластинку (рис 2.4.1) з провідникового матеріалу, вздовж якої проходить струм І. Якщо перпендикулярно площині пластини і напрямку струму діє магнітне поле напруженістю Н, то в пластині виникає ЕРС., пропорційна і струму, і напруженості магнітного поля:
Е=kІН, де k=kх/d – коефіцієнт, який залежить від матеріалу і товщини пластини d; kx – постійна Холла 
Напрямок цієї ЕРС., яка називається ЕРС. Холла, перпендикулярний струму і полю, тобто її можна виміряти між бічними повздовжними гранями пластини (рис. 2.4.1) за допомогою електровимірювального приладу. Причина появи ЕРС. Холла в тому, що на рухомі заряди в магнітному полі діє сила Лоренца. Струм в пластині – це і є упорядкований рух зарядів (в металі – електронів). Під дією магнітного поля вони зміщуються перпендикулярно напрямку свого руху і поблизу однієї повздовжньої грані виникає надлишок зарядів, а поблизу іншої – нестача. В звичайних провідникових матеріалах ЕРС. Холла дуже мала, що пояснюється малою швидкістю (точніше – рухомістю) носіїв струму через їх велику концентрацію. Хоча ефект Холла відомий вже більше ста років, практичне використання його почалось в результаті розвитку технології виготовлення напівпровідників. Саме в чистих напівпровідниках забезпечується висока рухомість носіїв струму, тому постійна Холла для чистих напівпровідників набагато більша, ніж для металів.
Эффект Холла, в некоторых случаях, позволяет определить тип носителей заряда (электронный или дырочный) в металле илиполупроводнике, что делает его незаменимым методом исследования свойств полупроводников.
На основе эффекта Холла работают датчики Холла: приборы, измеряющие напряжённость магнитного поля.
 2018-02-14
2018-02-14 2775
2775
