Библиографический список

ЕН. Ф. 01 МАТЕМАТИКА

Методические указания

И варианты заданий к контрольной работе № 1

 

Специальности: 250201 Лесное хозяйство

280402 Природоохранное обустройство территорий

 

 

Уфа 2009

УДК 51(07)

ББК 22.1я73,22.161.6

М 54

 

 

Рекомендовано к изданию методической комиссией факультета лесного хозяйства (протокол № 6 от 24.04.2009 года)

 

 

Составители:  доцент, к.соц.н. Саитова Р.З.

доцент, к.физ.-мат.н. Маннанов М.М.

 

Рецензент: доцент кафедры физики Юмагужин Р.Ю.

 

Ответственный за выпуск: зав. кафедрой математики

доцент, к.физ.-мат.н. Лукманов Р.Л.

ВВЕДЕНИЕ

 

Целью настоящих методических указаний является помощь студентам в освоении и закреплении следующих разделов математики: линейная и векторная алгебра, аналитическая геометрия.

Расчетно-графическая работа № 1 состоит из 5 заданий. В каждом задании 30 вариантов. Номер варианта студент выбирает по формуле: № = a · b + c, где a – номер задания, b и с – предпоследняя и последняя цифры шифра (номера зачетной книжки или студенческого билета).

Например, номер студенческого билета (зачетки) студента 1265. Тогда в первом задании этот студент выполняет вариант:
№ = 1 · 6 + 5 = 11. Во втором задании: № = 2 · 6 + 5 = 17 и т.д. Если получается вариант больше 30, то нужно вычитать 30. Например, для этого же студента третье задание будет высчитываться: 5 · 6 + 5 = 35. Следовательно, этот студент решает 35 – 30 = 5 – пятый вариант третьего задания.

Прежде чем приступать к выполнению работы, целесообразно изучить соответствующие разделы в учебниках, рекомендованных в библиографическом списке.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

 

Задача 2

Даны вершины треугольника ABC: A (– 2, 5), B (10, – 4), C (8, 10). Требуется найти: 1) длину стороны AB; 2) уравнения сторон AB и AC в общем виде и их угловые коэффициенты; 3) угол A в радианах;
4) уравнение медианы AD; 5) уравнение высоты CE и ее длину;
6) уравнение окружности, для которой высота CE есть диаметр и точки пересечения этой окружности со стороной AC.

Решение.

1. Расстояние d между точками A (х ₁; y ₁) и B (х ₂; y ₂) вычисляем по формуле:

                                    d =                                (1)

Применяя (1), находим длину стороны AB:

d_AB =  =  = 15.

2. Уравнение прямой, проходящей через точки A (х ₁; y ₁) и B (х ₂; y ₂), имеет вид:

                                           .                                       (2)

Подставив в (2) соответствующие координаты точек A и B находим уравнение прямой (AB):

 = ;  = ;

 = ; 4 y – 20 = – 3 x – 6; 3 x + 4 y – 14 = 0 (AB).

Чтобы найти угловой коэффициент прямой AB (k_AB), решим полученное уравнение прямой относительно y:

4 y = 3 x + 14,  откуда

Подставляя в (2) координаты точек A и C, находим уравнения прямой (AC):

 откуда

3. Если даны две прямые, угловые коэффициенты которых соответственно равны k ₁ и k ₂, то угол φ между этими прямыми определяется по формуле:

                                             .                                         (3)

Искомый угол A образован прямыми AB и AC, угловые коэффициенты которых найдены ранее в пункте 2. Для определения угла A положим  и . Применяя (3), получим:

  откуда .

Используя таблицу перевода градусной меры в радианную, получим A = 1,107 рад.

4. Если AD есть медиана, то точка D является серединой стороны BC. Для вычисления координат точки D применяем формулы деления отрезка на две равные части:

                                                                       (4)

Подставив в (4) координаты точек B и C, находим координаты точки D:

  D (9; 3).

Подставив в (2) координаты точек A (– 2; 5) и D (9; 3), находим искомое уравнение медианы AD:

2 x + 11 y – 51 = 0 (AD).

5. Высота CE перпендикулярна стороне AB. Известно, что если две прямые взаимно перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку. Следовательно, . Так как  то

Уравнение прямой, проходящей через данную точку, имеет вид:

                                                                                   (5)

Подставив в (5) координаты точки C и найденный угловой коэффициент , получим искомое уравнение высоты CE:

Чтобы найти длину CE, определим сперва координаты точки E – точки пересечения высоты CE и прямой AB. Для этого решаем совместно систему уравнений (AB) и (CE):

Решение этой системы дает x = 2 и y = 2. Следовательно, E (2; 2). Длину высоты CE определяем как расстояние между двумя точками по формуле (1).

d_CE = = 10.

6. Уравнение окружности с центром в точке K (a; b) и радиусом R имеет вид:

                                          (x – a)² + (y – b)² = R ².                                     (6)

По условию, высота CE служит диаметром искомой окружности. Следовательно, центр окружности K является серединой отрезка CE. Используя (4), находим координаты точки K.

  K (5; 6).

Так как d_CE = 10, то радиус окружности R = 5. Следовательно,
(x – 5)² + (y – 6)² = 25 – уравнение искомой окружности. Чтобы найти точки пересечения этой окружности с прямой AC, решаем совместную систему уравнений:

Решив эту систему, получим две точки пересечения C (8; 10) и М (0; 6). Треугольник ABC, медиана AD, высота CE, окружность с центром в точке K и точки ее пересечения со стороной AC построены в системе координат xOy на рис. 1.

 

Рисунок 1

 

Задача 3

На плоскости даны два вектора  = {2; – 3} и  = {1; 2}. Найти разложение вектора  = {9; 4} по базису  и .

Решение: Так как векторы  и  неколлинеарны, то вектор  можно единственным образом выразить через эти векторы:  = m  + n . Это соотношение и называется разложением вектора  по базису  и . Надо найти числа m и n. Для этого проделаем следующее:

 = 9  + 4 ,  = 2  – 3 ,  =  + 2 ,

тогда                      

отсюда                          

Окончательно,               = 2  + 5 .

 

Задача 4

Даны координаты вершин А (0; 0; 1), В (2; 3; 5), С (6; 2; 3), D (3; 7; 2) пирамиды ABCD. Требуется:

1) записать векторы  в системе орт , ,  и найти модули этих векторов;

2) найти угол между векторами ;

3) найти проекцию вектора  на вектор ;

4) найти площадь грани ABC;

5) найти объем пирамиды ABCD;

6) составить уравнение ребра AC;

7) составить уравнение грани ABC.

1. Известно, что произвольный вектор  представляется в системе орт , ,  по формуле

                                           = a_x  + a_y  + a_z ,                                     (1)

где a_x, a_y, a_z – координаты вектора  в системе координат, порожденной ортами, причем

a_x = np_Ox , a_y = np_Oy , a_z = np_Oz .

Если заданы точки M ₁(x ₁, y ₁, z ₁), M ₂(x ₂, y ₂, z ₂), то для вектора
 = .

,

то есть

                     .                 (2)

Воспользовавшись формулой (2) и координатами заданных точек А, В, С, D получим:

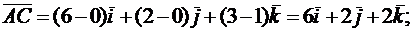
Если вектор  задан формулой (1), то его модуль вычисляется следующим образом:

                                                                                 (3)

Используя формулу (3), получаем модули найденных векторов:

2. Известна формула cos  =  где ·  – скалярное произведение векторов  и , которое можно вычислить следующим образом:

 ·  = .

У нас

cos φ = cos  =

то есть .

3. Известно, что

,

то есть в нашем случае

4. Воспользуемся формулой нахождения площади треугольника, построенного на векторах  и :

,

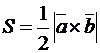где  – векторное произведение векторов, которое можно вычислить по следующему правилу:

.

В нашем примере , причем

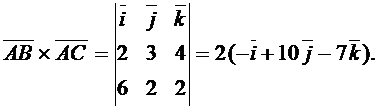
Таким образом,

 (кв.ед.).

5. Объем пирамиды, построенной на трех некомпланарных векторах , можно найти по формуле

где  – смешанное произведение векторов, которое вычисляется следующим образом:

.

У нас  где

то есть  (куб. ед.).

6. Известно, что уравнение прямой, проходящей через две заданные точки пространства и , имеет вид:

 

                                                                   (4)

 

Подставив в (4) координаты точек A и C, получим

 

 

то есть уравнение ребра AC окончательно запишется следующим
образом:

 

 или .

 

7. Уравнение плоскости, проходящей через три заданные точки  можно записать в виде:

 

 

Подставляя в него координаты точек A, B, C, получим

 

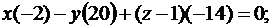
Задача 5

 

Составить уравнение геометрического места точек, отношение расстояний, которых до данной точки А (4; 0) и до данной прямой x = 1 равно 2.

Решение.

В системе координат xOy построим точку А(4; 0) и прямую х = 1.

Пусть М (х; у) – произвольная точка искомого геометрического места точек. Отпустим перпендикуляр МВ на данную прямую х = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то ее абсцисса равна 1, ордината точки В равна ординате точки В. Следовательно, В (1; у)

По условию задачи, МА: МВ = 2. Расстояния МА и МВ находим по формуле

 

 

Тогда имеем:

 

Возведя в квадрат левую и правую части, получим:

 

 или

 

Полученное уравнение представляет собой гиперболу, у которой действительная полуось равна 2, а мнимая равна  т.е.

 

a = 2, b = .

 

Определим фокусы гиперболы.

Для гиперболы выполняется равенство c ² = a ² + b ². Следовательно, c ² = 4 + 12 = 16, с = 4. F ₁(– 4; 0), F ₂(4; 0) – фокусы гиперболы. Заданная точка А (4; 0) является правым фокусом гиперболы.

Определим эксцентриситет полученной гиперболы:

Уравнение асимптот гиперболы имеет вид  и . Следовательно,  или ,  – асимптоты гиперболы.

 

 

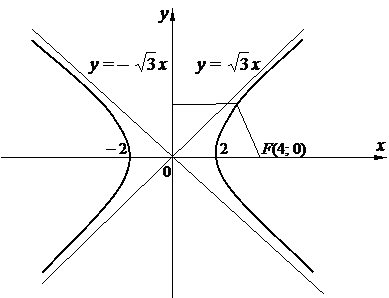
Рисунок 2

 

 

РАСЧЕТНЫЕ ЗАДАНИЯ

 

 

Задание № 2

1. Даны координаты вершин треугольника ABC. Требуется найти: 1) длину стороны AB; 2) уравнения сторон AB и AC в общем виде, их угловые коэффициенты; 3) угол A в радианах; 4) уравнение медианы AD; 5) уравнение высоты CE и ее длину; 6) уравнение окружности, для которой высота CE есть диаметр и точки пересечения этой окружности со стороной AC.

 

3.

А (– 2; – 6)

В (– 6; – 3)

С (10; – 1)

Задание № 3

1. Даны векторы ,  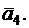Показать, что векторы ,  образуют базис трехмерного пространства и найти координаты вектора  в этом базисе.

 

	{– 1, 3, 5}	{5, – 1, 3}	{– 2, 9, – 2}	{8, 0, 1}

 

 

Задание № 4

Даны координаты вершин пирамиды ABCD. Требуется:

1) записать векторы  в системе орт  и найти модули этих векторов;

2) найти угол между векторами ;

3) найти проекцию вектора  на вектор ;

4) найти площадь грани ABC;

5) найти объем пирамиды ABCD;

6) составить уравнение ребра AC;

7) составить уравнение грани ABC.

 

	A	B	C	D
	{2; 3; 0}	{0; 6; 0}	{0; 3; 6}	{2; 6; 8}

Задание № 5

В задаче составить уравнение линии, для каждой точки которой ее расстояние до точки A (x ₁; y ₁) равно расстоянию до прямой y = b. Полученное уравнение привести к простейшему виду и построить кривую.

  А (2; 5), b = 1.

                                             

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Шипачев, В.С. Задачник по высшей математике: Учеб. пособие. – 2-е изд., испр. – М.: Высш. шк., 2003. – 304 с.

2. Данко, П.Е. и др. Высшая математика в упражнениях и задачах: в 2 ч. – М.: Высш. шк. ч. 1. – 1999. – 304 с.

3. Шипачев, В.С. Высшая математика: учеб. / Под ред. А.Н. Тихонова. – 2-е изд. стереотип. – М.: Высш. шк., 1998. – 479 с.

4. Письменный, Д.Т. Конспект лекций по высшей математике.
I, II ч. – М.: Рольф, 2002. – 288 с.

5. Зайцев, И.А. Высшая математика: учеб. – М.: Высш. шк., 1991. – 400 с.

 

Лицензия РБ на издательскую деятельность № 0261 от 10 апреля 1998 г.

Лицензия на полиграфическую деятельность № Б 848366 от 21.06.2000 г.

–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

Подписано в печать _________. Формат бумаги 60×84¹/₁₆

Усл. печ. л. 1,40. Уч.-изд. л. 1,28. Бумага офсетная

Печать трафаретная. Гарнитура «Таймс». Заказ _____. Тираж 200 экз.

–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

Издательство ФГОУ ВПО «Башкирский государственный аграрный университет»

Типография ФГОУ ВПО «Башкирский государственный аграрный университет»

Адрес издательства и типографии: 450001, г. Уфа, ул. 50-летия Октября, 34