Ответ: Это окружность

Задание 1

Функция  при любом значении x удовлетворяет соотношению

, где  – некоторое число. Докажите, что функция 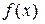 периодична.

 

Решение. Покажем, что 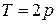 – период функции 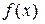. Находим,

 .

Функция

удовлетворяет условию задачи.

 

Задание 2

Найдется ли простое число , большее 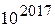, такое, что число  составное?

 

Ответ: Да.

Решение. Пусть  простое число, большее 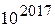. Прибавим  раз к нему число . Получим составное число . Ясно, что на одном из шагов прибавления  из некоторого простого числа  получилось составное.

 

Задание 3

Докажите, что  для некоторого многочлена  степени n с целыми коэффициентами.

 

Решение. Будем действовать по индукции, одновременно доказывая, что  для некоторого многочлена  степени n с целыми коэффициентами.

Интегрируя по частям (при ) имеем индукционный переход:

 

и

 

При  имеем .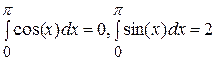

 

Задание 4

В -угольнике проведены все диагонали. Можно ли на сторонах и диагоналях поставить стрелки так, чтобы сумма получившихся векторов равнялась нулю?

 

Ответ: Всегда можно.

 

Решение. Все эти линии разбиваются на замкнутые ломаные: стороны многоугольника, если соединять через одну, если соединять через 2 (может образоваться одна или три замкнутые ломаные) и т.д. (При четном числе вершин возникают пары диаметрально противоположных точек, но у нас число вершин нечетное.)

Задание 5

Доказать неравенство

.

Решение. Рассмотрим три вектора . Пусть угол между векторами  и   равен 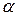, а между векторами  и  равен 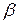. Тогда , , 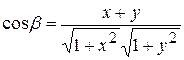. Следовательно,  и . Поэтому  

 

Задание 6

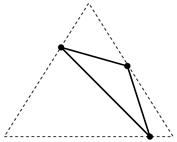Дан треугольник. Найти геометрическое место центров правильных треугольников, описанных около него (см. рисунок).

 

Ответ: Это окружность.

Решение. Пусть дан треугольник . Рассмотрим три правильных треугольника ,  и , построенных на сторонах ,  и  во внешнюю сторону, и их описанные окружности  (см. рисунок). Вершины любого правильного треугольника , описанного около треугольника , лежат на окружностях . Центр Z треугольника – точка пересечения двух биссектрис его углов  и . Эти биссектрисы пересекаются под углом 120 градусов и проходят через две фиксированные точки X и Y – середины дуг   и 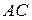 окружносте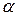й  и 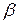, не содержащих точек  и 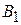. Т.е. искомое г.м.т. – окружность. Она проходит через точку Торричелли и середины дуг ,  и   окружностей .

 

 

Задание 7

a) Доказать, что наименьшее общее кратное чисел 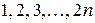 равно наименьшему общему кратному чисел .

Решение. Пусть  есть НОК , а  – НОК .

Покажем, что произвольное число d из множества чисел  делит . В самом деле, последовательно удваивая d, на некотором этапе мы попадем на отрезок . Получившееся число d’, кратное d и делит .

Поэтому  является наименьшим общим кратным и для чисел .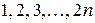

Задание 8

Пусть квадратная матрица A размером  такая, что для некоторого натурального  выполняется равенство .

Найти значение суммы , если  – ранг матрицы A, E –единичная матрица размером .

 

Ответ: 2017.

 

Решение. Заметим, что . Так как  (неравенство Сильвестра), то . С другой стороны, .  Следовательно, .