Задачи допуска к экзамену
Решение систем уравнений
Решить систему уравнений, используя формулы Крамера, матричный метод, метод Гаусса. Сделать проверку решения.
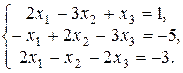
Аналитическая геометрия
1. Плоскость проходит через три точки 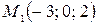 ,
, 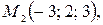
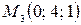 . Вычислить:
. Вычислить:
а) расстояние от точки 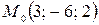 до данной плоскости;
до данной плоскости;
б) острый угол между данной плоскостью и плоскостью 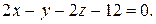
2. Даны две плоскости 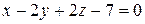 и
и 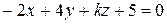 . При каких значениях k эти плоскости:
. При каких значениях k эти плоскости:
а) параллельны;
б) перпендикулярны?
3. Дан треугольник 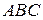 :
: 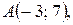
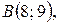
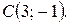 Найти:
Найти:
а) длину стороны 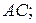
б) уравнение стороны 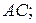
в) уравнение высоты 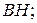
г) длину высоты 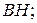
д) координаты точки Н;
е) уравнение медианы 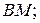
4. Найти радиус окружности и ее центр, если ее уравнение имеет вид:
в) 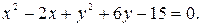
5. Составить каноническое уравнение эллипса, если:
а) его полуоси равны 5 и 3;
б) большая ось равна 10, а расстояние между фокусами равно 6;
в) расстояние между фокусами равно 12, а эксцентриситет равен 0,6;
г) большая ось равна 30, а эксцентриситет равен 0,6;
д) точка эллипса 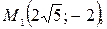 а малая ось равна 6; е) точки эллипса
а малая ось равна 6; е) точки эллипса 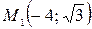 и
и 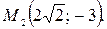
6. Составить каноническое уравнение параболы, если:
а) расстояние между фокусом и директрисой равно 4;
б) фокус находится в точке 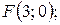 в) она проходит через точку
в) она проходит через точку 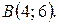
7. Составить уравнение линии на плоскости, каждая точка которой равноудалена от точки 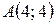 и от оси Ох.
и от оси Ох.
8. Составить уравнение линии на плоскости, каждая точка которой находится втрое ближе к точке 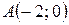 , чем к точке
, чем к точке 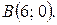
Преобразовать к каноническому виду уравнения, построить кривые, определить все характеристики полученной кривой:
9. 9 х 2+4 у 2 – 54 х – 32 у +109=0.
10. х 2 – у 2 – 4 х +2 у +7=0.
11. х 2 – 9 у 2+2 х – 36 у – 44=0.
12. у = х 2+4 х +5.
.
13. 4 х 2+9 у 2 – 8 х – 36 у +4=0.
Векторная алгебра
14. Даны векторы 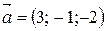 ,
, 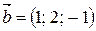 ,
, 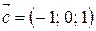 . Вычислить:
. Вычислить:
а) 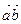 ;
;
б) 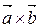 ;
;
в) 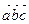 ;
;
г) 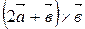 ;
;
д) 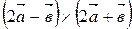 .
.
15. Даны координаты вершин пирамиды 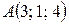 ,
, 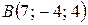 ,
, 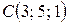 ,
, 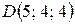 . Вычислить:
. Вычислить:
а) внутренний угол при вершине А в треугольнике АВС;
б) проекцию вектора 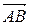 на направление вектора
на направление вектора 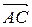 ;
;
в) площадь треугольника АВС;
г) длину высоты треугольника АВС, опущенной из вершины В на сторону АС; д) объем пирамиды АВСD.
16. Найти значение х при котором четыре точки 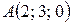 ,
, 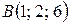 ,
, 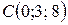 ,
, 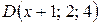 лежат в одной плоскости.
лежат в одной плоскости.
Пределы
17. 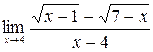 .
.
18. 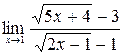 .
.
19. 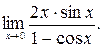
20. 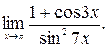
21. 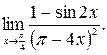
22. 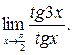
23. 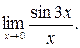
24. 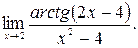
25. 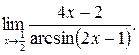
26. 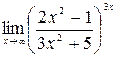 .
.
27. 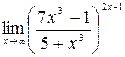 .
.
28. 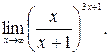
29. 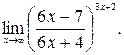
30. 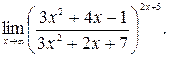
Производные
31. 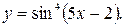
32. 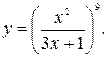
33. 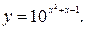
34. 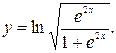
35. 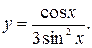
36. 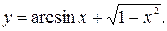
37. 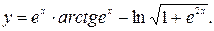
38. 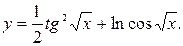
39. 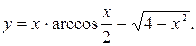
40. 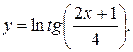
41. 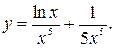
42. 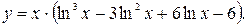
43. 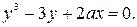
44. 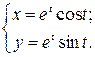 при
при 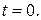
45. 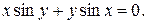
46. 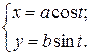
47. 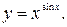
48. 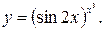
Найти производные второго порядка.
49. 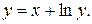
50. 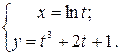
Уравнения касательной и нормали
Написать уравнения касательной и нормали к кривым в указанных точках.
51. 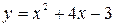 в точке (1;2).
в точке (1;2).
52. 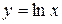 в точке пересечения с осью ОХ.
в точке пересечения с осью ОХ.
53. 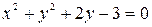 в точке (2,-1).
в точке (2,-1).
54. 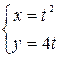 при
при 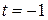 .
.
Найти дифференциалы функций.
55. 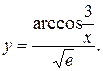
56. 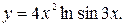
57. 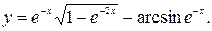
Ответы
1. а) 6; б) 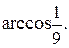 2. а) -4; б) 5.
2. а) -4; б) 5.
3. а) 10; б) 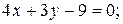 в)
в) 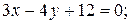 г) 10; д)
г) 10; д) 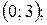
е) 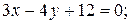
4. 5, 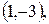
5. а) 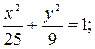 б)
б) 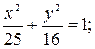 в)
в) 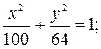
г) 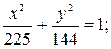 д)
д) 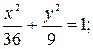 е)
е) 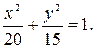
6. а) 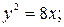 б)
б) 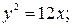 в)
в) 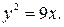
7. 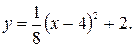
8. 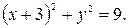 9.
9. 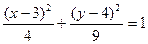 . 10.
. 10. 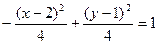 .
.
11. 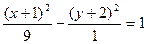 . 12. (х +2)2= у – 1. 13.
. 12. (х +2)2= у – 1. 13. 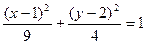 .
.
14. а) 3; б) 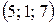 ; в) 2; г)
; в) 2; г) 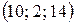 ; д) 50.
; д) 50.
15. а) 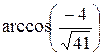 ; б) -4; в) 12,5; г) 5; д) 11.
; б) -4; в) 12,5; г) 5; д) 11.
16. 0,5. 17. 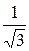 . 18.
. 18. 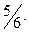
19. 4. 20. 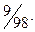 21.
21. 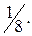 22.
22. 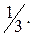 23. 3. 24.
23. 3. 24. 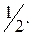 25. 2. 26. 0. 27.
25. 2. 26. 0. 27. 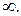
28. 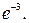 29.
29. 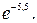 30.
30. 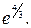
31. 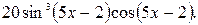 3 2.
3 2. 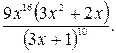 3 3.
3 3. 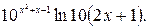 3 4.
3 4. 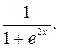
35. 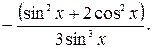
36. 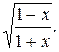 37.
37. 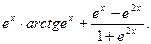
38. 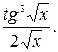 39.
39. 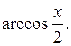 40.
40. 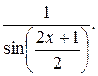
41. 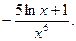 42.
42. 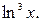 43.
43. 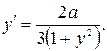 44. 1.
44. 1.
45. 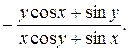
46. 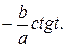 4 7.
4 7. 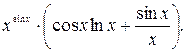 48.
48. 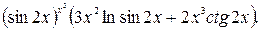
49. 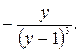
50. 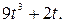
51. 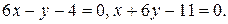
52. 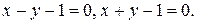 53.
53. 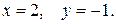 54.
54. 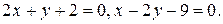
55. 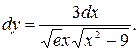
56. 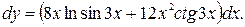 57.
57. 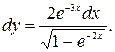
 2020-04-07
2020-04-07 125
125






