Алгоритм решения:
1. Уравнять основания логарифмов;
2. Сравнить подлогарифмические выражения:
- при 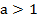 сохранить знак неравенства;
сохранить знак неравенства;
- при 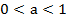 изменить знак неравенства на противоположный;
изменить знак неравенства на противоположный;
3. Учесть ОДЗ.
Пример 3. Решите неравенство: 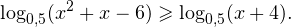
Решение. Основания логарифмов равны и меньше единицы, По схеме (2) получаем: первый аргумент меньше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее из них. Имеем систему 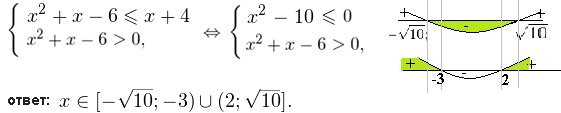
Пример 4. Решить неравенство: 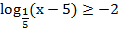 Решение. В левой части log, а в правой число. Приведем к виду logaf(x) ≥ logag(x). Для этого число в правой части представим в виде логарифма с тем же основанием, что логарифм в левой части, т.е.
Решение. В левой части log, а в правой число. Приведем к виду logaf(x) ≥ logag(x). Для этого число в правой части представим в виде логарифма с тем же основанием, что логарифм в левой части, т.е.
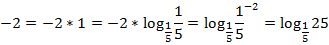 применили
применили 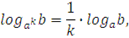
Итак, имеем неравенство: 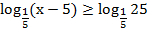
Основание логарифмов равны и меньше единицы, По схеме (2) получаем: первый аргумент меньше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее. Имеем систему:
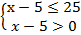 ó
ó 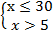
 Ответ:
Ответ: 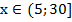
Пример 5. Решить неравенство log8(x2-4x+3)<1. Решение. В левой части log8t, а в правой 1. Приведем к виду logaf(x) < logag(x). Представим 1 в виде логарифма с тем же основанием, что логарифм в правой части, т.е. 1 = log88, тогда неравенство примет вид: log8(x2 – 4x + 3) < log88. Основание логарифмов равны и больше единицы, По схеме (1) получаем: первый аргумент меньше второго, по ОДЗ оба они больше нуля. Так как мы защищаем меньшее, то получим систему: 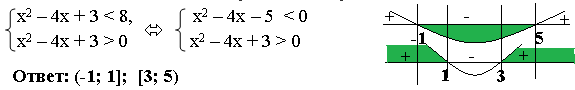
Логарифмические неравенства, сводящиеся к простейшим
Более сложные логарифмические неравенства сводятся к простейшим методами, аналогичными используемым при решении логарифмических уравнений.
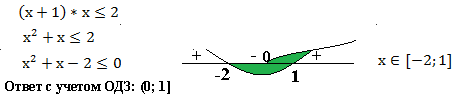
Пример 1. Решить неравенство: 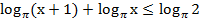
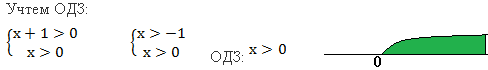 Согласно свойству логарифма преобразуем в левой части сумму логарифмов с одинаковым основанием в логарифм произведения:
Согласно свойству логарифма преобразуем в левой части сумму логарифмов с одинаковым основанием в логарифм произведения:
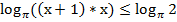
Нам известно, что число 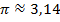 . Поэтому в равносильном неравенстве знак исходного неравенства сохраняется.
. Поэтому в равносильном неравенстве знак исходного неравенства сохраняется.
Пример 2. Решить неравенство: 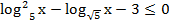
Решение: ОДЗ: х > 0. Видим два логарифма, но с разными основаниями. Приведем второй член к основанию 5. Получили неравенство:
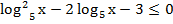 Очевидна замена:
Очевидна замена: 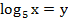
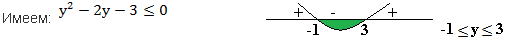 Вернемся к исходным переменным:
Вернемся к исходным переменным:
-1 ≤ log 5 x ≤ 3 . -1* -log55 ≤ log 5 x ≤ 3* log55
log55-1 ≤ log 5 x ≤ log553 
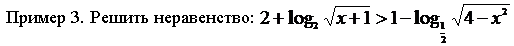 Решение. Преобразуем к простейшему логарифмическому неравенству. Видим два логарифма, основания разные; и в левой и в правой части есть числа. Перейдем к основанию 2 в выражении, стоящем в правой части данного неравенства, а числа запишем в виде логарифма:
Решение. Преобразуем к простейшему логарифмическому неравенству. Видим два логарифма, основания разные; и в левой и в правой части есть числа. Перейдем к основанию 2 в выражении, стоящем в правой части данного неравенства, а числа запишем в виде логарифма: 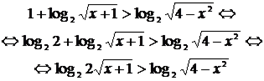 Основания одинаковые и больше 1.Функция log2 t – возрастающая, поэтому первый аргумент больше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее. Теперь перейдем к равносильной системе:
Основания одинаковые и больше 1.Функция log2 t – возрастающая, поэтому первый аргумент больше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее. Теперь перейдем к равносильной системе:
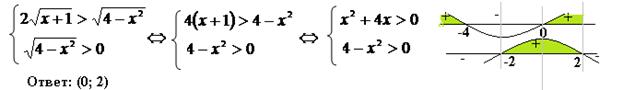
Если в неравенстве встречается логарифмическая функция, содержащая неизвестное в основании, то, как правило, следует рассматривать два случая: 1) когда основание больше 1, 2) когда основание положительно, но меньше 1.
Пример 4. Решить неравенство log x–3(x2-4x+3)<0.
Решение. Преобразуем правую часть в логарифм с требуемым основанием: 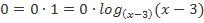 =
= 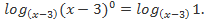 Имеем неравенство:
Имеем неравенство:
log x–3(x2 – 4x + 3) < log x–31. (простейшее неравенство) Так как основание логарифма содержит переменную, то рассмотрим два случая x-3>1 и 0<x-3<1. Если основание логарифма больше 1, то функция – возрастающая, поэтому первый аргумент меньше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее. Теперь перейдем к равносильной системе:
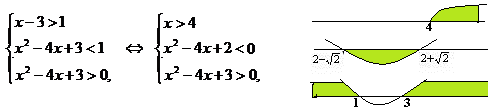 Совмещаем промежутки и видим, что данная система не имеет решений.
Совмещаем промежутки и видим, что данная система не имеет решений.
Рассмотрим второй случай, если 0 < x-3 < 1. Функция log(x-3)t – убывающая, поэтому, знак неравенства меняется. Для соблюдения ОДЗ достаточно защитить меньшее из аргументов. В этом случае получаем систему:
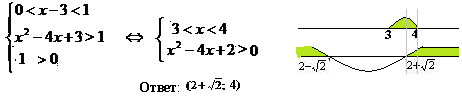
Пример 5. Решить неравенство 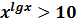
Решение. ОДЗ: х >0. Так как выражения, стоящие в левой и правой частях неравенства положительны, то для решения прологарифмируем обе части по основанию 10. Получим равносильное исходному неравенство:
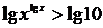 , пользуясь свойствами логарифмов lgx * lgx > 1
, пользуясь свойствами логарифмов lgx * lgx > 1
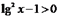 . Обозначим t = lg x и решим неравенство:.
. Обозначим t = lg x и решим неравенство:. 
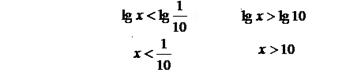
Учитывая ОДЗ х > 0  Ответ: (0; 0,1)È(10;+¥).
Ответ: (0; 0,1)È(10;+¥).
Пример 6. Решить неравенство 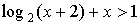
Решение. ОДЗ: х > -2. Если привести к простейшему виду logaf(x) > logag(x) не получим облегченного неравенства. Попробуем записать в виде:
log2(x + 2) > -x + 1. Это логарифмическо-линейное неравенство. Можно попробовать графический метод. Лучше использовать монотонность функции. В левой части монотонно возрастающая функция: f(x) = log2(x + 2), а в правой – монотонно убывающая: g(x) = -x + 1. Значит уравнение log2(x + 2) = -x + 1 имеет не более одного корня. Подбором находим что х = 0 есть корень этого уравнения. Проверим f(2)=2, a g(2)= -1. Значит правее х = 1 функция f(x) = log2(x + 2) больше чем g(x) = -x + 1. Ответ: х > 1.
Пример 7. Решите неравенство 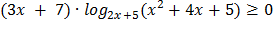
Решение. ОДЗ: 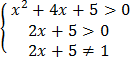 ó
ó 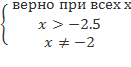
Очень часто бывает довольно несложное неравенство обычными преобразованиями трудно решить. Вот в таких случаях нам помогает универсальный метод - метод интервалов.
Нам надо избавиться от переменного основания, так как знак логарифмического выражения зависит как от аргумента, так и от основания. Пусть перейдем к основанию 2. Тогда имеем 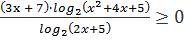 . Оно равносильно неравенству
. Оно равносильно неравенству
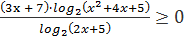 ó
ó 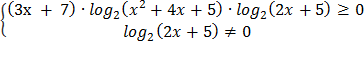
Рассмотрим функцию y = (3x + 7) 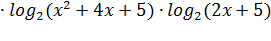
Находим нули функции:
3x + 7 = 0 или 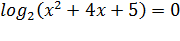
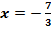 или
или 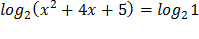
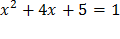
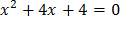
(x + 2)2 = 0
x = -2 (кратность равна 2)
Второе неравенство дает 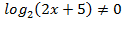 ó
ó 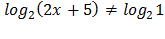 ó
ó
2x + 5 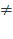 1 ó x
1 ó x  .
.
Видим х = -2 имеет кратность 3. Нули функции отметим на координатной прямой. Учитывая кратность нулей методом «тыка» находим знак функции.
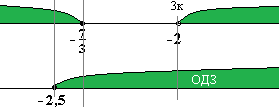 Ответ:
Ответ: 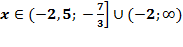
У метода интервалов есть свои минусы. Потому что не всегда удобно определять знаки на промежутках, тем более когда они малы, когда на них нет целых значений.
Пример 8. Решите неравенство 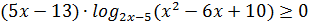
Решение. В этом случае применим метод равносильных преобразований. Это неравенство равносильно совокупности двух систем:
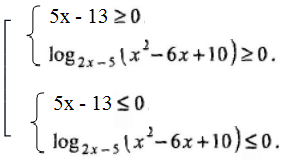
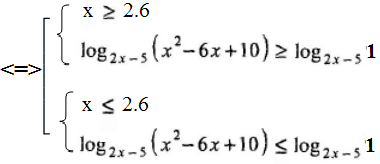 Первая система равносильно совокупности двух систем:
Первая система равносильно совокупности двух систем:
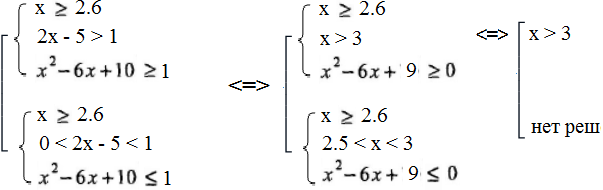
Итак решением первой системы будет промежуток (3;  ).
).
Также вторая система равносильно совокупности двух систем:
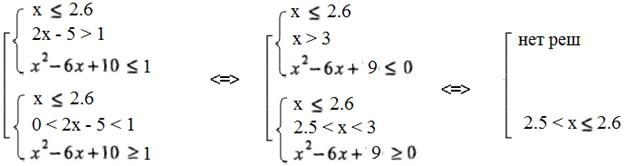
Решением второй системы будет промежуток 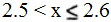
Таким образом, решением исходного неравенства 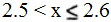 ; x > 3.
; x > 3.
Ответ. (2,5; 2,6]; (3;  )
)
 2020-04-12
2020-04-12 94
94






