Семинар №18
Цель семинара: изучить электромагнитные колебания и волны, их основные характеристики, условия возникновения.
1. Основные понятия и определения:
| Электромагнитны колебания – это периодические изменения во времени электрического заряда, силы тока, напряжения, энергии электрического и магнитного полей. Простейшей системой, в которой возникают электромагнитные колебания, является колебательный контур, который состоит из конденсатора емкостью C и катушки с индуктивностью L (рис. 1). |  |
Если заряженный конденсатор подключить к катушке, то в цепи колебательного контура начнет протекать ток. Через некоторое время заряд конденсатора станет равным нулю, ток через катушку достигнет максимального значения и начнется процесс зарядки конденсатора, и т.д., возникнут свободные электромагнитные колебания. Если пренебречь сопротивлением катушки и соединительных проводов, то такие колебания будут совершаться бесконечно долго, их называют незатухающими. В действительности, любые свободные колебания со временем прекратятся, будут затухающими, механические – благодаря силе трения, электромагнитные – за счет нагревания проводов при протекании электрического тока.
Характеристики электромагнитных колебаний аналогичны характеристикам механических колебаний. Амплитуда колебаний A – наибольшее значение колеблющейся физической величины. В электромагнитных колебаниях периодически изменяются заряд и напряжение конденсатора, сила тока в катушке. В этом случае говорят об амплитудах заряда  [Кл], напряжения
[Кл], напряжения  [В] и силы тока
[В] и силы тока 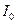 [А]. Также можно рассматривать колебания энергии электрического
[А]. Также можно рассматривать колебания энергии электрического  и магнитного
и магнитного  полей.
полей.
Период Т, частота v, циклическая частота ω электромагнитных колебаний эквивалентны соответствующим характеристикам механических колебаний. Они также связаны соотношениями: 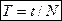 , где N – число полных колебаний за время t,
, где N – число полных колебаний за время t,  ,
,  .
.
Свободные незатухающие электромагнитные колебания в колебательном контуре являются гармоническими, то есть, изменения во времени физических величин, характеризующих эти колебания, происходят по закону синуса или косинуса.
Заряд конденсатора в колебательном контуре изменяется по закону  , где q 0 – амплитуда заряда. Взяв первую производную от заряда, получаем уравнение для колебаний силы тока в катушке:
, где q 0 – амплитуда заряда. Взяв первую производную от заряда, получаем уравнение для колебаний силы тока в катушке: 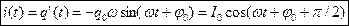 , где
, где  – амплитуда силы тока. Если взять вторую производную от заряда,
– амплитуда силы тока. Если взять вторую производную от заряда, 
 , то можно получить дифференциальное уравнение электромагнитных колебаний:
, то можно получить дифференциальное уравнение электромагнитных колебаний:  . Функция
. Функция  является его решением.
является его решением.
Напряжение на конденсаторе определяется формулой  , где
, где  – амплитуда напряжения. Из дифференциального уравнения следует, что
– амплитуда напряжения. Из дифференциального уравнения следует, что  . Таким образом период колебаний в колебательном контуре определяется формулой Томсона:
. Таким образом период колебаний в колебательном контуре определяется формулой Томсона:  .
.
Превращение энергии в электромагнитных колебаниях. При свободных незатухающих электромагнитных колебаниях система получает энергию только в начальный момент времени (например, при зарядке конденсатора), а далее энергия, а с ней и амплитуда колебаний не меняются. В каждый момент времени сумма энергий электрического и магнитного полей в колебательном контуре не меняется, т.е. полная энергия колебательного контура остается постоянной:  .
.
Энергия электрического и магнитного полей при колебаниях в контуре переходят друг в друга за четверть периода. Когда заряд на конденсаторе максимален, энергия электрического поля максимальна, а энергия магнитного поля катушки равна нулю. При полной разрядке конденсатора, наоборот, энергия электрического поля равна нулю, а энергия магнитного поля максимальна.
 – энергия электрического поля конденсатора,
– энергия электрического поля конденсатора,  – энергия магнитного поля катушки и
– энергия магнитного поля катушки и
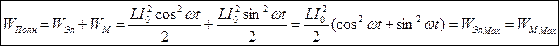 .
.
Следует отметить, что энергия электрического и магнитного поля изменяется с удвоенной частотой колебаний относительно уровня равного половине полной энергии колебательной системы (рис. 2 и 3):


 и
и  .
.
Можно провести аналогию между механическими и электромагнитными колебаниями.
| Механические колебания | Электромагнитные колебания |
Величина отклонения, x 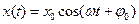 | Заряд, q 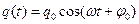 |
Скорость, V 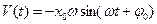 | Сила тока, I  |
| Коэффициент возвращающей силы, k | Величина, обратная емкости конденсатора,  |
| Масса, m | Индуктивность катушки, L |
Потенциальная энергия,  | Энергия электрического поля,  |
Кинетическая энергия,  | Энергия магнитного поля,  |
Электромагнитные волны – это распространяющиеся в пространстве электромагнитные колебания. Вокруг колеблющегося, движущегося с ускорением, заряда возникает переменное электрическое поле, которое порождает переменное магнитное поле, которое, в свою очередь, порождает вихревое электрическое поле и т. д. Так порождается и распространяется в пространстве электромагнитная волна.
Электромагнитная волна является поперечной, вектор напряженности электрического поля E и вектор индукции магнитного поля B в электромагнитной волне перпендикулярны друг другу и направлению распространения волны (рис. 4).
 Расстояние, которое волна проходит за период, называют длиной волны:
Расстояние, которое волна проходит за период, называют длиной волны:  . Скорость распространения электромагнитной волны в вакууме равна скорости света
. Скорость распространения электромагнитной волны в вакууме равна скорости света 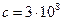 м/с. В среде скорость распространения электромагнитной волны уменьшается в n раз, где n – абсолютный показатель преломления среды:
м/с. В среде скорость распространения электромагнитной волны уменьшается в n раз, где n – абсолютный показатель преломления среды:  . Показатель преломления воздуха близок к единице
. Показатель преломления воздуха близок к единице  , поэтому можно считать, что скорость электромагнитной волны в воздухе близка к скорости света в вакууме.
, поэтому можно считать, что скорость электромагнитной волны в воздухе близка к скорости света в вакууме.
2. Базовые задачи:
1. В колебательном контуре напряжения на обкладках конденсатора меняется по закону  [В]. Емкость конденсатора равна
[В]. Емкость конденсатора равна  = 26 нФ. Определите период и частоту электромагнитных колебаний, индуктивность колебательного контура, зависимость тока i (t) и заряда q (t) от времени, максимальную энергию электрического и магнитного поля. Определите силу тока в катушке в момент времени, когда заряд конденсатора уменьшился в 2 раза от амплитудного значения.
= 26 нФ. Определите период и частоту электромагнитных колебаний, индуктивность колебательного контура, зависимость тока i (t) и заряда q (t) от времени, максимальную энергию электрического и магнитного поля. Определите силу тока в катушке в момент времени, когда заряд конденсатора уменьшился в 2 раза от амплитудного значения.
Решение
Из зависимости напряжения от времени  видно, что циклическая частота колебаний равна
видно, что циклическая частота колебаний равна  . Следовательно, период колебаний равен
. Следовательно, период колебаний равен  c, а частота –
c, а частота –  =103 Гц.
=103 Гц.
Индуктивность контура найдем из формулы Томсона:

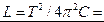
 Гн.
Гн.
Зависимость заряда и тока от времени найдем из соотношений:
 . Подставляя числовые значения, получим:
. Подставляя числовые значения, получим:
 [А],
[А],  [Кл].
[Кл].
Максимальная энергия как электрического поля, так и магнитного равны между собой:
 Дж.
Дж.
Для определения тока в катушке запишем закон сохранения энергии в колебательном контуре  . Отсюда получаем:
. Отсюда получаем:  . В итоге
. В итоге  1,4 А.
1,4 А.
2. Индуктивность и емкость колебательного контура равны L и C соответственно. Через какое время после начала зарядки конденсатора его энергия в N раз превышает энергию катушки индуктивности?
Решение
Запишем закон изменения напряжения и силы тока в контуре:  ,
,  . Выражения для энергии электрического и магнитного поля имеют вид:
. Выражения для энергии электрического и магнитного поля имеют вид:  и
и  . По условию задачи
. По условию задачи  , то есть
, то есть  .
.
Отсюда получим:  . Из закона сохранения энергии в контуре следует, что
. Из закона сохранения энергии в контуре следует, что

 , и
, и  . Следовательно,
. Следовательно, 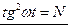 . Циклическая частота колебаний в контуре равна
. Циклическая частота колебаний в контуре равна  . В итоге получим, что
. В итоге получим, что  .
.
3. Колебательный контур радиоприемника настроен на частоту  = 6 МГц. Во сколько раз нужно изменить емкость конденсатора контура, чтобы он был настроен на длину волны
= 6 МГц. Во сколько раз нужно изменить емкость конденсатора контура, чтобы он был настроен на длину волны 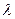 = 25 м?
= 25 м?
Решение
Колебательный контур настроен на частоту ν 0 или на длину волны 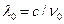 , где с – скорость света. Частота его собственных колебаний равна
, где с – скорость света. Частота его собственных колебаний равна  , отсюда емкость конденсатора равна
, отсюда емкость конденсатора равна 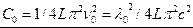 . Отсюда видно, что емкость конденсатора пропорциональна квадрату длины волны
. Отсюда видно, что емкость конденсатора пропорциональна квадрату длины волны  . Первоначально приемник настроен на длину волны
. Первоначально приемник настроен на длину волны  = 50 м. Следовательно, для того, чтобы настроить приемник на частоту
= 50 м. Следовательно, для того, чтобы настроить приемник на частоту 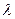 = 25 м =
= 25 м =  (меньше в 2 раза), емкость конденсатора колебательного контура необходимо уменьшить
(меньше в 2 раза), емкость конденсатора колебательного контура необходимо уменьшить 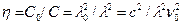 = 4 раза.
= 4 раза.
 2020-04-12
2020-04-12 2305
2305