Основные свойства неопределенного интеграла

Г.

Лекция № 5

 ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.

Первообразная функция. Понятие неопределенного интеграла.

Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Интегральное исчисление решает обратную задачу — нахождение самой функции по ее производной или дифференциалу.

Функция 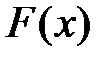 называется первообразной функцией для функции на промежутке 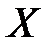, если в каждой точке  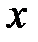этого промежутка .

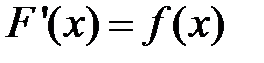Например,  является первообразной для функции 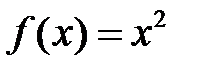, так как .

Следует отметить, что для заданной функции ее первообразная определена неоднозначно. Дифференцируя, нетрудно убедиться, что все функции 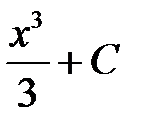, где   — некоторое число, являются первообразными для функции .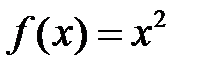

 Аналогично в общем случае, если 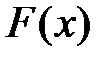— некоторая первообразная для , то, поскольку 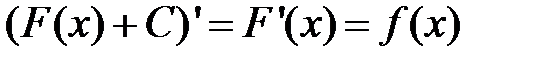, функции вида , где  - произвольное число, также являются первообразными для . 

Совокупность всех первообразных для функции 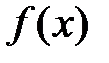на промежутке 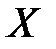называется неопределенным интегралом от функции 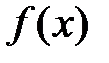и обозначается 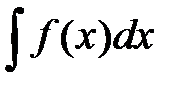, где 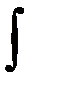  — знак интеграла,  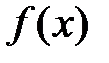— подынтегральная функция,  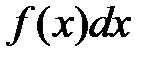— подынтегральное выражение. Таким образом,

                                 

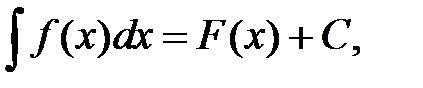
где 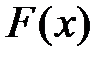 — некоторая первообразная для 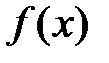, — произвольная постоянная.

Например, 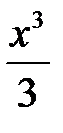 - первообразная для функции 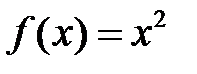, то .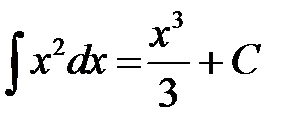

Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.

Основные свойства неопределенного интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции, т.е,

                                 .

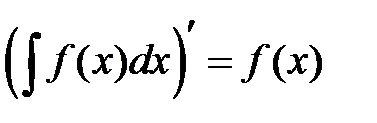2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.

                               .

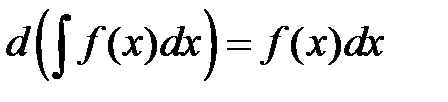3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

                                  

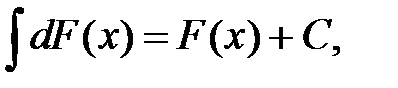
где  — произвольное число.

4. Постоянный множитель можно выносить за знак интеграла, т.е.

                               

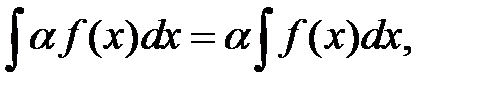
где 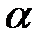 — произвольное число.

5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.

                   

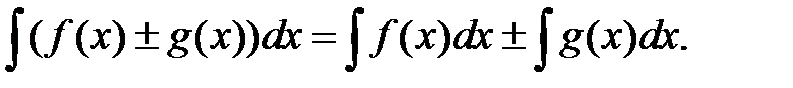
Перечислим интегралы от элементарных функций, которые в дальнейшем мы будем называть табличными:

                                         

                            

                                    

                          

                                     

                                

                                 

                

                      

                      

                   

                                   

                                .

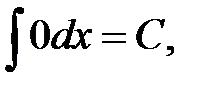
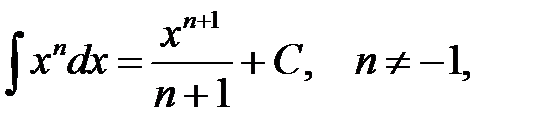
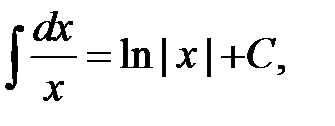
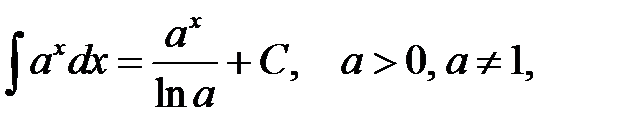
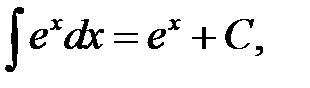
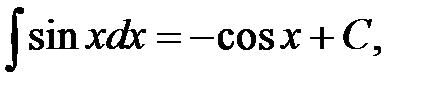
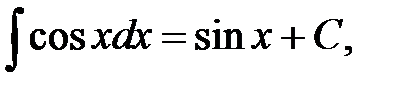
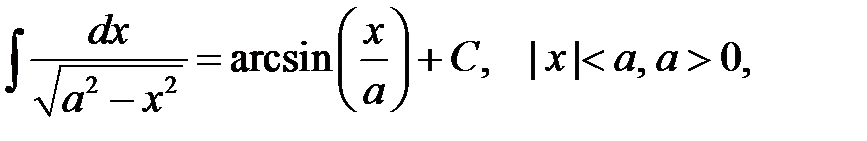
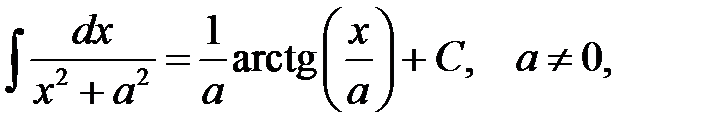
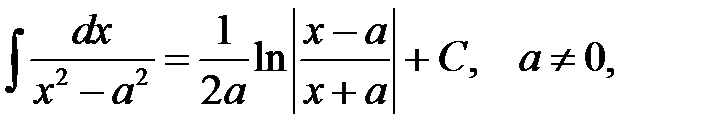
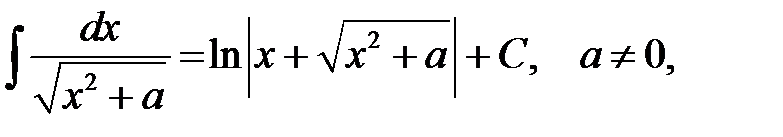
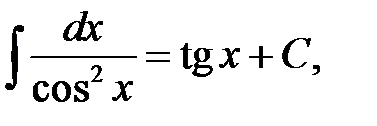
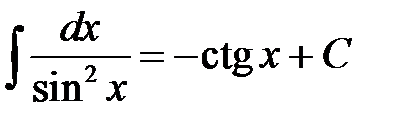Пример 1:  Найти .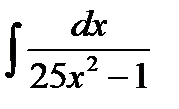

Решение.

= .

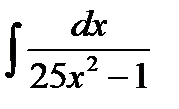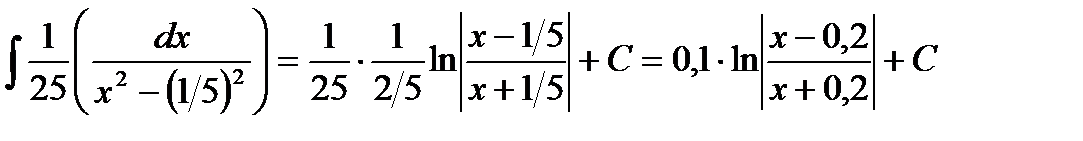Пример 2: Найти неопределенный интеграл .

Используя пятое свойство неопределенного интеграла, вынесем за знак интеграла постоянную 2. Затем, выполняя элементарные математические преобразования, приведем подынтегральную функцию к степенному виду:

.

 

Домашнее задание: Конспект лекций.