Метод замены переменной в неопределенном интеграле

ЗОТ группа МЦМ-19, Математика                               15.04.2020

Тема: Интегрирование методом замены переменной.

Задание:

Изучить новый материал. Записать в тетрадь опорный конспект  с решением примеров.

2. Решить задание № 5 из своей контрольной работы ( кто сдал контрольную, то на отдельном листе, кто не сдал (это залет), то в контр. тетради).

Фото выполненной работы СЕГОДНЯ отправлять ТОЛЬКО по этой ссылке в ВК: https://vk.com/topic-193913663_41388847

 

 

Таблица первообразных. Вычисление неопределенных интегралов.

(У вас есть в методичке по математике)

Функция    f(x)	Первообразная     F(x)	Пример
0	С
1	х + С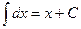
k – (число)	kx + C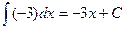
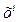
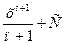
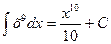
x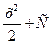
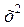
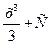
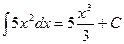
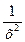
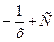
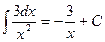
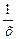
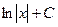
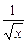
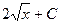
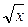
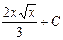
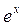
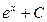
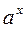
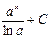
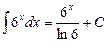
sin x	- cos x +C
cos x	sin x+C
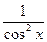
	tg x +C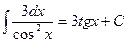
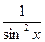
	- ctg x+C

Метод замены переменной в неопределенном интеграле

Переходим к рассмотрению общего случая – метода замены переменных в неопределенном интеграле.

Пример 1

Найти неопределенный интеграл.

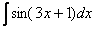
Это интеграл сложной функции. Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой.
В данном случае напрашивается: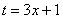
Вторая по популярности буква для замены – это буква .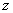
В принципе, можно использовать и другие буквы, но мы всё-таки будем придерживаться традиций.

Итак: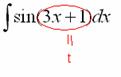
Но при замене у нас остаётся 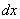! Наверное, многие догадались, что если осуществляется переход к новой переменной 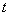, то в новом интеграле всё должно быть выражено через букву 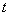, и дифференциалу 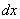там совсем не место.
Следует логичный вывод, что 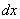нужно превратить в некоторое выражение, которое зависит только от .

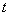Действие следующее. После того, как мы подобрали замену, в данном примере, 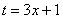, нам нужно найти дифференциал 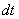. С дифференциалами, думаю, дружба уже у всех налажена.

Так как 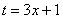, то

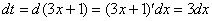
После разборок с дифференциалом окончательный результат рекомендую переписать максимально коротко: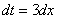
Теперь по правилам пропорции выражаем нужный нам :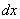

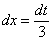
В итоге: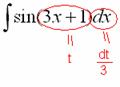
Таким образом:

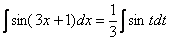
А это уже самый что ни на есть табличный интеграл 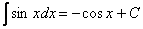(таблица интегралов, естественно, справедлива и для переменной ).

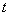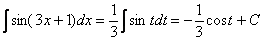
В заключении осталось провести обратную замену. Вспоминаем, что .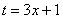

Готово.

Чистовое оформление рассмотренного примера должно выглядеть примерно так:

“

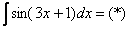
Проведем замену: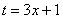

“

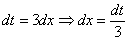
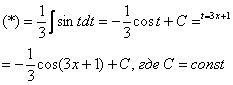
Значок не несет никакого математического смысла, он обозначает, что мы прервали решение для промежуточных объяснений.

Также всем рекомендую использовать математический знак вместо фразы «из этого следует это». И коротко, и удобно.

 
  Пример 2

Найти неопределенный интеграл.

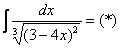
Проведем замену: 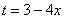(другую замену здесь трудно придумать)

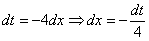
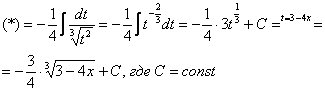
Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл.

 

 

Пример 3

Найти неопределенный интеграл.

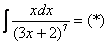
Замена: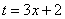
Осталось выяснить, во что превратится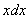

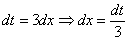
Хорошо, 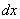мы выразили, но что делать с оставшимся в числителе «иксом»?!
Время от времени в ходе решения интегралов встречается следующий трюк: 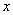мы выразим из той же замены !

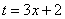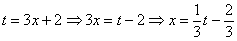
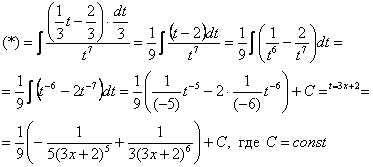
Готово.

Пример 4

Найти неопределенный интеграл.

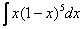
Решение:

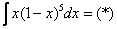
Замена: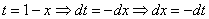

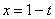
Пример 5

Найти неопределенный интеграл.

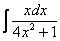
Настало время рассказать об основной предпосылке использования метода замены переменной: в подынтегральном выражении должна находиться некоторая функция 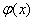и её производная 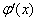: 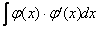(функции 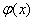, 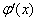могут быть и не в произведении)

В этой связи при нахождении интегралов довольно часто приходится заглядывать в таблицу производных.

В рассматриваемом примере замечаем, что степень числителя на единицу меньше степени знаменателя. В таблице производных находим формулу 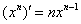, которая как раз понижает степень на единицу. А, значит, если обозначить за 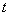знаменатель, то велики шансы, что числитель 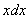превратится во что-нибудь хорошее.

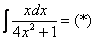
Замена: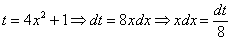

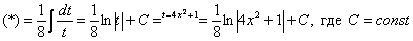
Кстати, здесь не так сложно подвести функцию под знак дифференциала:

 

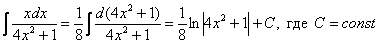
Пример 6

Найти неопределенный интеграл.

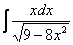
Решение:

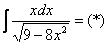
Проведем замену:

 

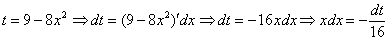
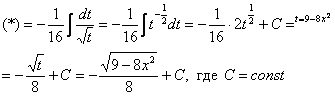
Пример 7

Найти неопределенный интеграл.

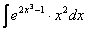
Решение:

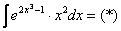
Проведем замену:

 

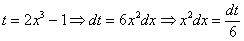
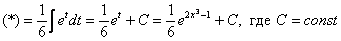
ИТАК, обобщим! Удобней всего заменять на букву t  внутреннюю часть сложной функции, потом от нее найти производную (дифференциал) dt. И составить новую простую функцию с буквой t.