Вам необходимо выучить определение и формулы

Геометрическая прогрессия.

Тип урока: урок  усвоения новых знаний и первичного закрепления.

Цель урока:  формирование понятия геометрической прогрессии;

                   познакомить со свойствами геометрической прогрессии и формулой

                   n-го члена;

                  закрепить полученные знания на примерах решения задач.

Используемые ресурсы: видеофильмы с онлайн-уроками,

                                        конспект-инструкция для учащихся.

Деятельность учащихся: во время просмотра видео и чтения конспекта-инструкции

                                         делаем в тетради записи.

Инструкция:

1. На последних занятиях мы изучали арифметическую прогрессию. Сегодня знакомимся с новой последовательностью. Смотрим видео – объяснение, но:

              определение пишем из учебника стр.229,

             формулу пишем тоже из учебника ;

далее оформляем в тетради вывод формулы n-го члена в тетради (видео «1 часть»).

2.Установим важное свойство членов геометрической прогрессии:

разбираем вывод в учебнике стр.230-231 или можно посмотреть и записать

замечательный вывод из видео (видео «2 часть»)

записываем формулировку, две формулы (для решения задач можно

использовать любую) и разобранный пример.

     или (если все члены положительны).

 

Основные формулы:

1)  - из определения

                                           2)      - знаменатель (чтобы его найти нужно

                                 следующий член прогрессии разделить на предыдущий)

                                            3) - формула n-го члена

                                            4) 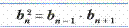 или -свойство г.п.

3.Учимся применять эти формулы.

1) Разобрать решение примеры 1 и 2 из учебника стр.231-232.

2) Посмотрите(можно не списывать) образец!!! решения для №819:

  Дано: (b_n) – г.п.

              b₈ =16; q = ¾

  Найти: b₇

 Решение: b₈ = b₇ ∙ q

                   b₇ = b₈: q = 16: ¾= 16 ∙ 4/3 = 64/3 = 21

                   Ответ: b₇= 21

Посмотрите (можно не списывать) образец!!! решения для №826:

    Дано: (у_n) – г.п.

              у₁ =64; q = - 1/2

  Найти: у₃; у₆

 Решение: у₃ = у₁ ∙ q² = 64 ∙ (-1/2)²=….. (и далее считаем)

                   у₆ = у₁ ∙ q⁵ = ……. (подставляем и считаем)

                   Ответ: …. (пишем)

 

3) Решить из учебника по этим образцам: № 821, 823, 825, 828, 830, 

                                                                      *832 (подсказка: выразить каждый член

                                                                        прогрессии через первый и знаменатель,

                                                                        доказать равенство).

4) Вспомните как мы выражали:

 в арифметической прогрессии:           а в геометрической прогрессии будет

у₃ = у₁ + 2d                                                         у₃ = у₁ ∙ q²

    у₇ = у₄ + 3d                                                         у₇ = у₄ ∙ q³

  Выполнить № 834, 835

Подводим итог:

Вам необходимо выучить определение и  формулы.