Бесконечно убывающая геометрическая прогрессия

РАЗДЕЛ 8. НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА

ТЕМА: Суммирование последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма.

Цель занятия: узнать, что называется геометрической прогрессией и формулу суммы ее членов.

Порядок выполнения работы:

1) Изучить теоритический материал, составить конспект в тетради;

2) В течение пары выполнить задания по материалу лекции (решить в тетради и выслать фотографии или документ преподавателю в социальной сети или на личную почту);

Контакты преподавателя: Arina_Kozlova96@mail.ru; https://vk.com/rina1996

Теоретический материал для самостоятельного изучения

Геометрическая прогрессия - это еще один частный случай числовых последовательностей.

Геометрической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.

Очевидно, что первый член последовательности, и, следовательно, все ее члены, отличны от нуля.

Число называется знаменателем геометрической прогрессии.

Основное свойство геометрической прогрессии.

· квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних:

Формула n-го члена геометрической прогрессии:

ВАЖНО! Зная первый член и знаменатель геометрической прогрессии, можно найти любой ее член.

Несложно получить формулу суммы n членов геометрической прогрессии.

... (1)

Умножим обе части равенства на

... (2)

Вычтем из равенства (2) равенство (1). Получим:

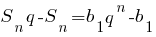(остальные слагаемые в правой части равенства взаимно уничтожатся)

Отсюда получаем формулу суммы n членов геометрической прогрессии:

(1)

Бесконечно убывающая геометрическая прогрессия

Если знаменатель геометрической прогрессии , то каждый следующий член прогрессии по модулю меньше предыдущего.

Такая геометрическая прогрессия называется бесконечно убывающей.

Сумму членов бесконечно убывающей геометрической прогрессии мы находим по формуле:

(2)

ВАЖНО! Формулу суммы членов бесконечно убывающей геометрической прогрессии (2) мы используем только в том случае, если в условии в явном виде указано, что нужно найти сумму бесконечного числа членов. Если указано конкретное число n, то пользуемся формулой (1) суммы n членов, даже если .

Практические задания

Задание 1. Какие из данных последовательностей являются геометрическими прогрессиями?

1) 2; 4; 8; 16; …

2) –8; –8; –8; –8; …

3) 6; –6; 6; –6; …

4) 7; 11; 15; 19; …

5) –3,2; –2,5; –1,8; –1,1; …

6) 2; 2,3; 2,34; 2,345; …

Задание 2. Дана геометрическая прогрессия