2020-05-21
107Апреля
Классная работа
Перпендикулярность прямых, прямой и плоскости, плоскостей.
В классной работе:
Повторить и выписать в тетрадь по учебнику: основные формулировки теорем из главы 2 параграф 1-3.
2.Записать в тетрадь задачи из экзаменационного материала:
№28(2 часть) Найти площадь прямоугольной трапеции, большее основание которой равно 14 см, большая боковая сторона – 12 см, а острый угол равен 
.
Решение:
В прямоугольной трапеции ABCD ВС || AD – основания, 
, AD = 14 см, CD = 12 см, 
. Проведем высоту трапеции СМ, 
.
Из 
:
(см),
(см).
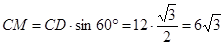(см). Так как ABCМ – прямоугольник, то 
см. 
см2.
Ответ: 
см2.
№6(2 часть). В цилиндре на расстоянии 8 см от его оси и параллельно ей проведено сечение, диагональ которого равна 13 см. Вычислите радиус основания цилиндра, если его высота равна 5 см.
Решение:
В данном цилиндре ОО 1 – высота цилиндра.. Его сечение параллельно оси ОО 1, а значит, является прямоугольником, стороны которого 
– образующие, 
– хорды оснований. По условию 
см, 
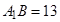см. Так как сечение параллельно оси, то 
плоскость сечения перпендикулярно плоскости основания и АВ – их линия пересечения. В плоскости основания проведем 
, тогда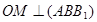 
. Так же 
. Значит, ОМ – расстояние между осью цилиндра и плоскостью сечения, тогда 
см.
|
|
|
Рассмотрим 
:по теоремы Пифагора имеем
(см)
Так как 
как радиусы, то 
– равнобедренный с основанием АВ. Тогда его высота ОМ, проведенная к основанию является медианой и 
(см).
Из 
: по теореме Пифагора имеем
(см).
Ответ: 10 см.
№4(3 часть). В основании пирамиды лежит прямоугольный треугольник с катетом а и противолежащим острым углом α. Боковые ребра пирамиды образуют с плоскостью основания угол φ. Найдите объем пирамиды.
Решение:
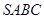– треугольная пирамида, в основании которой лежит прямоугольный треугольник 
, 
, 
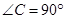и противолежащий угол 
. 
– высота пирамиды, 
, тогда SA, SB и SC – наклонные, а ОA, ОB и ОC – соответственно их проекции на плоскость основания. Значит,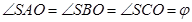 
, как углы образованные боковыми ребрами с плоскостью основания (АВС). Так как , то 
, 
, 
. Тогда 
по общему катету и острому углу 
. Следовательно, 
и точка О является центром окружности, описанной около . Так как этот треугольник прямоугольный, то точка О – середина гипотенузы АВ.
Найдем объем пирамиды по формуле 
, где
– площадь основания, 
;
Н – высота пирамиды, 
.
Из 
: 
, 
.
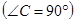Так как точка О – середина гипотенузы АВ, то 
.
.
Из 
: 
.
.
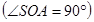Ответ: 
.
3.Решить задания из 1 части:
Домашнее задание: повторить главы 2 параграф 1-3, решить задания из ГИА:
1) №29(2 часть)Найти площадь прямоугольной трапеции, меньшее основание которой равно 7 см, большая боковая сторона – 16 см, а тупой угол равен 
|
|
|
2) №7(2 часть). В цилиндре параллельно его оси проведено сечение, диагональ которого равна 17 см. Высота цилиндра 15 см, а радиус основания 5 см. На каком расстоянии от оси проведено это сечение?
3) №26(3 часть).Основанием пирамиды служит прямоугольный треугольник с острым углом β и гипотенузой с. Каждое боковое ребро пирамиды составляет с основанием угол α. Найдите объем пирамиды.
Если у вас вопросы-пишите личным сообщением.
Учитель: Борюшова Елена Алексеевна.
