Лекции: элементы теории графов

1. Основные понятия теории графов.

Определение 1. Неориентированный граф  задается множествами вершин 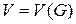 и ребер , , а каждое ребро  есть неупорядоченная пара вершин 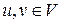, т. е. 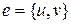. Ребро e называется звеном, если (оно имеет два конца), и петлей, если .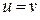

Вершины графа G, соединенные ребром, называются смежными, как и два ребра, инцидентные одной вершине. Кратными ребрами называются звенья, имеющие одинаковые пары концов. Граф без петель и кратных ребер называется простым. Графы, содержащие кратные ребра, называют мультиграфами, а петли и кратные ребра – псевдографами.

Определение 2. Ориентированный граф (орграф)  задается множествами вершин 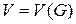 и дуг , , а каждая дуга  есть упорядоченная пара вершин 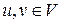, иначе, .

Для преобразования графа G в орграф каждое его ребро заменяют двумя дугами, имеющими противоположную ориентацию. Граф G называется конечным, если множества  и  конечны, т. е. при и 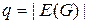 имеем  и .

Граф 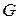 называется двудольным, если , где  и – два непересекающихся непустых множества, а все вершины из  смежны только вершинам из .

Дополнением  графа G называется граф, в котором две вершины смежны тогда и только тогда, когда они не смежны в G.

Геометрическим изображением графа служит его диаграмма.

Терминология теории графов еще не стандартизирована. Вместо терминов "вершина" и "ребро" в теории электрических цепей соответственно применяются термины "узел" и "ветвь", а в топологии – "точка" и "линия".

По определению орграф определяет бинарное отношение. Поэтому он широко используется и в математике, большая часть которой может быть описана на языке бинарных отношений.

Годом рождения теории графов считают 1736 год, когда Эйлер решил знаменитую задачу о кёнигсбергских мостах.

Известным примером графа является граф выпуклого многогранника, вершины и ребра которого рассматриваются соответственно в качестве вершин и ребер графа. Электрическая цепь, карта дорог, генеалогическое дерево, программа для ЭВМ и т. п. также дают примеры графов.

Перечислим ряд простых графов: 1) нуль-граф (пустой граф) не имеет ни ребер, ни вершин, 2) граф-вершина имеет одну вершину и не имеет ребер, 3) граф-петля состоит из единственной петли и ее одного конца, 4) граф-звено состоит из единственного звена и двух его концов.

5) n -кликой,  (полным графом) называется простой граф , имеющий ровно n вершин и  ребер, в котором каждая пара вершин смежна. Так, – нуль-граф, – граф-вершина, – граф-звено.

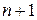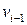6) n -цепью,  называется простой граф  с n ребрами и  вершинами, причем его ребрам можно приписать номера от 1 до n, а вершинам – от 0 до n так, чтобы концами ребра  были вершины  и , , т. е. задать естественную нумерацию. Так, – граф-звено.

7) n -циклом,  называется простой граф  с n ребрами и n вершинами, причем им можно приписать номера от 1 до n так, чтобы концами ребра  были вершины  и , , . Так, – граф-петля, а  часто называют треугольником. Число n для  и  называется их длиной.

8) Полным двудольным графом называется двудольный граф , для которого ,  и  смежна с .

Для простых графов, мультиграфов и псевдографов дадим

Определение 3. Степенью  вершины v в графе G называется число ребер, инцидентных этой вершине, причем для петли .

В соответствии с данным определением для любых графов имеет место

Теорема 1. ,

установленная Эйлером, из которой вытекают

Следствие 1. В любом графе число вершин нечетной степени четно.

Следствие 2. Каждый кубический граф 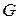 (граф, у которого ) имеет четное число вершин.

Эта теорема и ее следствия являются старейшими и широко известными результатами из теории графов.

При  вершина v называется изолированной, при – висячей или концевой. Граф 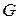 называется n -однородным (n -регулярным), если 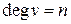. Так, – 2-однородный граф, а – ()-однородный граф.

2. Матрицы смежности и инцидентности.

Определения 1 и 2 соответственно описывают компьютерные представления графа и орграфа. Другие важные компьютерные представления графов задают специальные матрицы, полностью определяющие эти графы.

Определение 1. Матрица  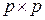называется матрицей смежности неориентированного мультиграфа 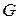,  равно числу ребер, соединяющих вершину графа  с , причем . В псевдографе для вершины  с петлей . Для орграфа 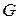 равен числу дуг, идущих из  в .

Определение 2. Матрица  размера  называется матрицей инцидентности неориентированного мультиграфа 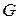, причем ее элементы

а для орграфа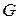

Эти матрицы имеют многочисленные применения.

Упражнение. а) Для графов тетраэдра, куба, октаэдра найти основные характеристики: число вершин, число ребер, последовательность степеней вершин, найти матрицу смежности и матрицу инцидентности.

б) Для  при  найти основные характеристики: число вершин, число ребер, последовательность степеней вершин; найти матрицу смежности и матрицу инцидентности.

в) Для графов  и  определить основные характеристики: число вершин, число ребер, последовательность степеней вершин; найти матрицу смежности и матрицу инцидентности.

3. Изоморфизм графов. Теорема о вложении всевдографа в R³.

Введем следующее важное понятие

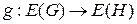Определение 1. Пусть G и H – графы, а  и  соответствующие биекции. Пара  называется изоморфизмом (изоморфным отображением) графа G на граф H, если вершина v инцидентна ребру e в графе G  вершина fv инцидентна ребру ge в графе H.

Если изоморфизм q существует, то графы G и H называются изоморфными. Можно рассматривать q как операцию и писать . Также удобно писать 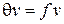 для каждой вершины и  для каждого ребра графа G. Отношение изоморфизма является отношением эквивалентности и разбивает класс всех графов на непустые и непересекающиеся множества графов. Для изомофных графов G и H имеем  и .

Если графы G и H совпадают, то изоморфизм q называется автоморфизмом. В частности, всякий граф имеет тождественный (тривиальный) автоморфизм.

Теорема 1. Пусть G и H – простые графы, а  биекция, обладающая следующим свойством: две различные вершины  графа G смежны  смежны их образы  в графе H. Тогда существует биекция 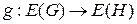 такая, что пара – изоморфизм графа G на граф H.

Доказательство Т1 следует из простоты графов и О1, а Т1 позволяет определить изоморфизм простых графов как биекцию их вершин, сохраняющую отношение смежности.

Следствие 1. Если простые графы  и  изоморфны, то  и  также изоморфны.

Теорема 2. Любой псевдо граф G = (V, E) может быть вложен в  так, чтобы его ребра не пересекались между собой.

4. Подграфы. Действия над подграфами. Компоненты графа.

Построение графа можно проводить, начиная с 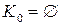 (или любого другого), путем добавления нужных вершин и ребер, а также, исходя из  (или любого другого), путем удаления нужных вершин и ребер.

Последний алгоритм построения графа приводит к понятию подграфа: граф , содержащийся в графе 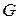, называется подграфом графа 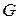. Точнее это записывается с помощью выражений: 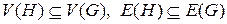, а каждое ребро  имеет в графе 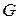 те же концы, что и в .

Рассмотрим следующее правило построения подграфов:

Теорема 1. Пусть G –граф, . В графе G существует подграф H, для которого 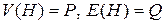 концы  содержатся в P.

Графы  могут представлять собой подграфы графа G.

Определение 1. Подграф H графа G называется остовным, если . Остовный n -регулярный подграф графа G называется n -фактором.

Клика  в мультиграфе G, у которого , является -фактором. Каждый граф G содержит пустой подграф , который не является остовным подграфом никакого графа G, кроме нуль-графа.

Пусть K и L – подграфы графа G, не обязательно различные. В силу правила построения подграфов можно определить объединение  с помощью соотношений: 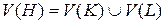,  и пересечение , для которого , 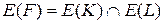. Подграфы K и L графа G называются непересекающимися, если .