Примеры решения задач к теме 4. ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ
Пример 4.1. После года хранения на складе в среднем 10% аккумуляторов выходит из строя. Определить вероятность того, что после года хранения из 12 аккумуляторов окажутся годными:
а) 10,
б) больше половины.
Решение.
Проводится 12 независимых испытаний, состоящих в проверке годности аккумулятора. Для каждого из 12 аккумуляторов вероятность события А – аккумулятор после года хранения годный – по условию постоянна и равна: 
А. Требуется определить вероятность того, что из 12 аккумуляторов ровно 10 будут годными, т. е. вероятность  . Поскольку испытания удовлетворяют условиям схемы Бернулли, то эту вероятность можно определить по формуле Бернулли (1.24):
. Поскольку испытания удовлетворяют условиям схемы Бернулли, то эту вероятность можно определить по формуле Бернулли (1.24):

Б. Требуется определить вероятность того, что из 12 аккумуляторов более 12/2=6 будут годными, т. е. вероятность  . При этом по теореме сложения для несовместных событий (1.13):
. При этом по теореме сложения для несовместных событий (1.13):
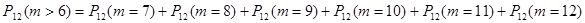 ,
,
так как события  не совместны.
не совместны.
Так как испытания удовлетворяют условиям схемы Бернулли, то вероятности можно определить по формуле Бернулли (1.24):
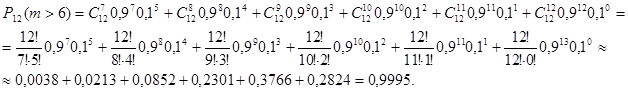
Пример 4.2. Вероятность своевременного выполнения заказа цехами службы быта равна 0,75. Найти вероятность того, что из 160 заказов своевременно выполнят:
а) 120;
б) не менее 110.
Решение.
Проводится 160 независимых испытаний, состоящих в проверке выполнения заказа цехами службы быта. Для каждого из 160 заказов вероятность события А - заказ выполнен - по условию постоянна:
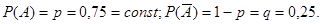
В задаче число испытаний n=160, р=0,75, npq=160*0,75*0,25=30  20.
20.
А. Требуется определить вероятность того, что из 160 заказов своевременно выполнят 120, т. е. вероятность 
Так как испытания удовлетворяют условиям схемы Бернулли, n велико, р отлична от 0 и 1, npq  20, то эту вероятность можно определить в соответствии с локальной теоремой Муавра – Лапласа (1.25):
20, то эту вероятность можно определить в соответствии с локальной теоремой Муавра – Лапласа (1.25):
 , где
, где  .
.
Получим  , откуда, по табл. 7 плотности вероятности нормированного нормального закона распределения, находим f(0)=0,3989.
, откуда, по табл. 7 плотности вероятности нормированного нормального закона распределения, находим f(0)=0,3989.
В результате искомая вероятность того, что из 160 заказов своевременно будет выполнено ровно 120:

Б. Требуется определить вероятность того, что из 160 заказов своевременно выполнят не менее 110, т. е. вероятность  .
.
Так как испытания удовлетворяют условиям схемы Бернулли, n велико, р отлична от 0 и 1, npq  20, то эту вероятность можно определить в соответствии с интегральной теоремой Муавра – Лапласа (1.26):
20, то эту вероятность можно определить в соответствии с интегральной теоремой Муавра – Лапласа (1.26):
 где
где 
Получим 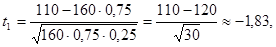

откуда по табл. 1 Приложений значений функции Лапласа нормированного нормального закона распределения, находим:
Ф(-1,83)=-Ф(1,83)=-0,9327, Ф(7,3)=1.
В результате искомая вероятность того, что не менее 110 из 160 заказов будут выполнены своевременно равна:

Пример 4.3. При обработке линз в среднем 3 из 100 имеют брак. Сколько линз следует обработать, чтобы с вероятностью 0,95 можно было ожидать, что отклонение доли брака от его вероятности не превысит 0,01 (по абсолютной величине)?
Решение.
Проводятся независимые испытания, состоящие в проверке брака обработки линз. Для каждой линзы вероятность события А – линза обработана с браком – по условию постоянна и равна:

В задаче надежность  =0,95, отклонение
=0,95, отклонение  =0,01.
=0,01.
Требуется определить число линз п, которые необходимо обработать. Так как испытания удовлетворяют условиям схемы Бернулли, то количество линз можно определить в соответствии со вторым следствием интегральной теоремы Муавра –Лапласа (1.28):

По табл. 1 Приложений значений функции нормированного нормального закона распределения, находим  откуда
откуда 
Следовательно, нужно обработать n=1118 линз, чтобы с вероятностью 0,95 можно было утверждать, что отклонение доли появления бракованной линзы от вероятности быть бракованной (равной 0,03) не превысит 0,01 (по абсолютной величине).
Пример 4.4. Вероятность изготовления бракованной отливки равна 0,002. Определить вероятность того, что из выпущенных 500 отливок количество бракованных составит:
а) 2;
б) более двух.
Решение.
Проводится 500 независимых испытаний, состоящих в проверке брака отливки. Для каждой из 500 отливок вероятность события А – отливка бракованная - по условию постоянна и равна:

В задаче число испытаний велико n=500, р=0,002 – мала, параметр Пуассона 
А. Требуется определить вероятность того, что из 500 отливок ровно 2 будут бракованными, т. е. вероятность 
Так как испытания удовлетворяют условиям схемы Бернулли, n>>100, р – мала,  то эту вероятность можно определить по формуле Пуассона (1.31):
то эту вероятность можно определить по формуле Пуассона (1.31):

(вероятность можно определить и по табл. 8 Приложений значений функции Пуассона для  и m=2).
и m=2).
Б. Требуется определить вероятность того, что из 500 отливок более 2 будут бракованные, т. е. вероятность 
При этом по теореме сложения для несовместных событий (1.13):

так как события  несовместны. В данном случае целесообразно перейти к противоположному событию (что будет не больше 2 бракованных отливок,
несовместны. В данном случае целесообразно перейти к противоположному событию (что будет не больше 2 бракованных отливок,  ), и воспользоваться следствием (1.15):
), и воспользоваться следствием (1.15):

Так как испытания удовлетворяют условиям схемы Бернулли, n>>100, р – мала,  , то вероятности можно определить по формуле Пуассона (1.31):
, то вероятности можно определить по формуле Пуассона (1.31):

ПРИЛОЖЕНИЯ
Приложение А
Значения* функции 
| х | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0,0 | 3989 | 3989 | 3989 | 3988 | 3986 | 3984 | 3982 | 3980 | 3980 | 3973 |
| 0,1 | 3970 | 3965 | 3961 | 3956 | 3951 | 3945 | 3939 | 3932 | 3925 | 3918 |
| 0,2 | 3910 | 3902 | 3894 | 3885 | 3876 | 3867 | 3857 | 3847 | 3836 | 3825 |
| 0,3 | 3814 | 3802 | 3790 | 3778 | 3765 | 3752 | 3739 | 3725 | 3712 | 3697 |
| 0,4 | 3683 | 3668 | 3653 | 3637 | 3621 | 3605 | 3589 | 3572 | 3555 | 3538 |
| 0,5 | 3521 | 3503 | 3485 | 3467 | 3448 | 3429 | 3410 | 3391 | 3372 | 3352 |
| 0,6 | 3332 | 3312 | 3292 | 3271 | 3251 | 3230 | 3209 | 3187 | 3166 | 3144 |
| 0,7 | 3123 | 3101 | 3079 | 3056 | 3034 | 3011 | 2989 | 2966 | 2943 | 2920 |
| 0,8 | 2897 | 2874 | 2850 | 2827 | 2803 | 2780 | 2756 | 2732 | 2709 | 2685 |
| 0,9 | 2661 | 2637 | 2613 | 2589 | 2565 | 2541 | 2516 | 2492 | 2468 | 2444 |
| 1,0 | 2420 | 2396 | 2371 | 2347 | 2323 | 2299 | 2275 | 2251 | 2227 | 2203 |
| 1,1 | 2179 | 2155 | 2131 | 2107 | 2083 | 2059 | 2036 | 2012 | 1989 | 1965 |
| 1,2 | 1942 | 1919 | 1895 | 1872 | 1845 | 1826 | 1804 | 1781 | 1758 | 1736 |
| 1,3 | 1714 | 1691 | 1669 | 1647 | 1626 | 1604 | 1582 | 1561 | 1539 | 1518 |
| 1,4 | 1497 | 1476 | 1456 | 1435 | 1415 | 1394 | 1374 | 1354 | 1334 | 1315 |
| 1,5 | 1295 | 1276 | 1257 | 1238 | 1219 | 1200 | 1182 | 1163 | 1145 | 1127 |
| 1,6 | 1109 | 1092 | 1074 | 1057 | 1040 | 1023 | 1006 | 0989 | 0973 | 0957 |
| 1,7 | 0940 | 0925 | 0909 | 0893 | 0878 | 0863 | 0848 | 0833 | 0818 | 0804 |
| 1,8 | 0790 | 0775 | 0761 | 0748 | 0734 | 0721 | 0707 | 0694 | 0681 | 0669 |
| 1,9 | 0656 | 0644 | 0632 | 0620 | 0608 | 0596 | 0584 | 0573 | 0562 | 0551 |
| 2,0 | 0540 | 0529 | 0519 | 0508 | 0498 | 0488 | 0478 | 0468 | 0459 | 0449 |
| 2,1 | 0440 | 0431 | 0422 | 0413 | 0404 | 0396 | 0387 | 0379 | 0371 | 0363 |
| 2,2 | 0355 | 0347 | 0339 | 0332 | 0325 | 0317 | 0310 | 0303 | 0297 | 0290 |
| 2,3 | 0283 | 0277 | 0270 | 0264 | 0258 | 0252 | 0246 | 0241 | 0235 | 0229 |
| 2,4 | 0224 | 0219 | 0213 | 0208 | 0203 | 0198 | 0194 | 0189 | 0184 | 0180 |
| 2,5 | 0175 | 0171 | 0167 | 0163 | 0158 | 0154 | 0151 | 0147 | 0143 | 0139 |
| 2,6 | 0136 | 0132 | 0129 | 0126 | 0122 | 0119 | 0116 | 0113 | 0110 | 0107 |
| 2,7 | 0104 | 0101 | 0099 | 0096 | 0093 | 0091 | 0088 | 0086 | 0084 | 0081 |
| 2,8 | 0079 | 0077 | 0075 | 0073 | 0071 | 0069 | 0067 | 0065 | 0063 | 0061 |
| 2,9 | 0060 | 0058 | 0056 | 0055 | 0053 | 0051 | 0050 | 0048 | 0047 | 0046 |
| 3,0 | 0044 | 0033 | 0024 | 0017 | 0012 | 0009 | 0006 | 0004 | 0003 | 0002 |
| 4,0 | 0001 | 0001 | 0001 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 |
* Все значения умножены на 10 000.
Приложение Б
Значения* функции 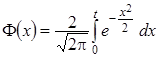
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,00 | 00000 | 00798 | 01596 | 02393 | 03191 | 03988 | 04784 | 05581 | 06376 | 07171 |
| 0,1 | 07966 | 08759 | 09552 | 10348 | 11134 | 11924 | 12712 | 13499 | 14285 | 15069 |
| 0,2 | 15852 | 16633 | 17413 | 18191 | 18967 | 19741 | 20514 | 21284 | 22052 | 22818 |
| 0,3 | 23582 | 24344 | 25103 | 25860 | 26614 | 27366 | 28115 | 28862 | 29605 | 30346 |
| 0,4 | 31084 | 31819 | 32552 | 33280 | 34006 | 34729 | 35448 | 36164 | 36877 | 37587 |
| 0,5 | 38292 | 38995 | 39694 | 40387 | 41080 | 41768 | 42452 | 43132 | 43809 | 44481 |
| 0,6 | 45149 | 45814 | 46474 | 47131 | 47783 | 48431 | 49075 | 49714 | 50350 | 50981 |
| 0,7 | 51607 | 52230 | 52848 | 53461 | 54070 | 54675 | 55275 | 55870 | 56461 | 57047 |
| 0,8 | 57629 | 58206 | 58778 | 59346 | 59909 | 60468 | 61021 | 61570 | 62114 | 62653 |
| 0,9 | 63188 | 63718 | 64243 | 64763 | 65278 | 65789 | 66294 | 66795 | 67291 | 67783 |
| 1,0 | 68269 | 68750 | 69227 | 69699 | 70166 | 70628 | 71086 | 71538 | 71986 | 72429 |
| 1,1 | 72867 | 73300 | 73729 | 74152 | 74571 | 74986 | 75395 | 75800 | 76200 | 76595 |
| 1,2 | 76986 | 77372 | 77754 | 78130 | 78502 | 78870 | 79233 | 79592 | 79945 | 80295 |
| 1,3 | 80640 | 80980 | 81316 | 81648 | 81975 | 82298 | 82617 | 82931 | 83241 | 85547 |
| 1,4 | 83849 | 84146 | 84439 | 84728 | 85013 | 85294 | 85571 | 85844 | 86113 | 86378 |
| 1,5 | 86639 | 86696 | 87149 | 87398 | 87644 | 87886 | 88124 | 88358 | 88589 | 88817 |
| 1,6 | 89040 | 89260 | 89477 | 89690 | 89899 | 90106 | 90309 | 90508 | 90704 | 90897 |
| 1,7 | 91087 | 91273 | 91457 | 91637 | 91814 | 91988 | 92159 | 92327 | 92492 | 92655 |
| 1,8 | 92814 | 92970 | 93124 | 93275 | 93423 | 93569 | 93711 | 93852 | 93989 | 94124 |
| 1,9 | 94257 | 94387 | 94514 | 94639 | 94762 | 94882 | 95000 | 95116 | 95230 | 95341 |
| 2,0 | 95450 | 95557 | 95662 | 95764 | 95865 | 95964 | 96060 | 96155 | 96247 | 96338 |
| 2,1 | 96427 | 96514 | 96599 | 96683 | 96765 | 96844 | 96923 | 96999 | 97074 | 97148 |
| 2,2 | 97219 | 97289 | 97358 | 97425 | 97491 | 97555 | 97618 | 97679 | 97739 | 87798 |
| 2,3 | 97855 | 97911 | 97966 | 98019 | 98072 | 98123 | 98172 | 98221 | 98269 | 98315 |
| 2,4 | 98360 | 98405 | 98448 | 98490 | 98531 | 98571 | 98611 | 98649 | 98686 | 98723 |
| 2,5 | 98758 | 98793 | 98826 | 98859 | 98891 | 98923 | 98953 | 98983 | 99012 | 99040 |
| 2,6 | 99068 | 99095 | 99121 | 99146 | 99171 | 99195 | 99219 | 99241 | 99263 | 99285 |
| 2,7 | 99307 | 99327 | 99347 | 99367 | 99386 | 99404 | 99422 | 99439 | 99456 | 99473 |
| 2,8 | 99489 | 99505 | 99520 | 99535 | 99549 | 99563 | 99576 | 99590 | 99602 | 99615 |
| 2,9 | 99627 | 99639 | 99650 | 99661 | 99672 | 99682 | 99692 | 99702 | 99712 | 99721 |
| 3,0 | 99730 | 99739 | 99747 | 99755 | 99763 | 99771 | 99779 | 99786 | 99793 | 99800 |
| 3,1 | 99806 | 99813 | 99819 | 99825 | 99831 | 99837 | 99842 | 99848 | 99853 | 99858 |
| 3,2 | 99863 | 99867 | 99872 | 99876 | 99880 | 99885 | 99889 | 99892 | 99896 | 99900 |
| 3,3 | 99903 | 99907 | 99910 | 99913 | 99916 | 99919 | 99922 | 99925 | 99928 | 99930 |
| 3,4 | 99933 | 99935 | 99937 | 99940 | 99942 | 99944 | 99946 | 99948 | 99950 | 99952 |
| 3,5 | 99953 | 99955 | 99957 | 99958 | 99960 | 99961 | 99963 | 99964 | 99966 | 99967 |
| 3,6 | 99968 | 99969 | 99971 | 99972 | 99973 | 99974 | 99975 | 99976 | 99977 | 99978 |
| 3,7 | 99978 | 99979 | 99980 | 99981 | 99982 | 99982 | 99983 | 99984 | 99984 | 99985 |
| 3,8 | 99986 | 99986 | 99987 | 99987 | 99988 | 99988 | 99989 | 99989 | 99990 | 99990 |
| 3,9 | 99990 | 99991 | 99991 | 99992 | 99992 | 99992 | 99992 | 99993 | 99993 | 99993 |
* Все значения умножены на 100 000.
Приложение В
Таблица значений функции Пуассона

| m | λ | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 |
| 0 | 0,9048 | 0,8187 | 0,7408 | 0,6703 | 0,6065 | 0,5488 | 0,4966 | 0,4493 | 0,4066 | |
| 1 | 0,0905 | 0,1638 | 0,2222 | 0,2681 | 0,3033 | 0,3293 | 0,3476 | 0,3596 | 0,3696 | |
| 2 | 0,0045 | 0,0164 | 0,0333 | 0,0536 | 0,0758 | 0,0988 | 0,1217 | 0,1438 | 0,1647 | |
| 3 | 0,0002 | 0,0011 | 0,0033 | 0,0072 | 0,0126 | 0,0198 | 0,0284 | 0,0383 | 0,0494 | |
| 4 | – | – | 0,0002 | 0,0007 | 0,0016 | 0,0030 | 0,0050 | 0,0077 | 0,0111 | |
| 5 | – | – | – | 0,0001 | 0,0002 | 0,0004 | 0,0007 | 0,0012 | 0,0020 | |
| 6 | – | – | – | – | – | – | 0,0001 | 0,0002 | 0,0003 | |
|
| ||||||||||
|
| ||||||||||
| m | λ | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 |
| 0 | 0,3679 | 0,1353 | 0,0498 | 0,0183 | 0,0067 | 0,0025 | 0,0009 | 0,0003 | 0,0001 | |
| 1 | 0,3679 | 0,2707 | 0,1494 | 0,0733 | 0,0337 | 0,0149 | 0,0064 | 0,0027 | 0,0011 | |
| 2 | 0,1839 | 0,2707 | 0,2240 | 0,1465 | 0,0842 | 0,0446 | 0,0223 | 0,0107 | 0,0055 | |
| 3 | 0,0313 | 0,1804 | 0,2240 | 0,1954 | 0,1404 | 0,0892 | 0,0521 | 0,0286 | 0,0150 | |
| 4 | 0,0153 | 0,0902 | 0,1618 | 0,1954 | 0,1755 | 0,1339 | 0,0912 | 0,0572 | 0,0337 | |
| 5 | 0,0081 | 0,0361 | 0,1008 | 0,1563 | 0,1755 | 0,1606 | 0,1277 | 0,0916 | 0,0607 | |
| 6 | 0,0005 | 0,0120 | 0,0504 | 0,1042 | 0,1462 | 0,1606 | 0,1490 | 0,1221 | 0,0911 | |
| 7 | 0,0001 | 0,0034 | 0,0216 | 0,0595 | 0,1044 | 0,1377 | 0,1490 | 0,1396 | 0,1318 | |
| 8 | – | 0,0009 | 0,0081 | 0,0298 | 0,0655 | 0,1033 | 0,1304 | 0,1396 | 0,1318 | |
| 9 | – | 0,0002 | 0,0027 | 0,0132 | 0,0363 | 0,0688 | 0,1014 | 0,1241 | 0,0318 | |
| 10 | – | – | 0,0008 | 0,0053 | 0,0181 | 0,0413 | 0,0710 | 0,0993 | 0,1180 | |
| 11 | – | – | 0,0002 | 0,0019 | 0,0082 | 0,0225 | 0,0452 | 0,0722 | 0,0970 | |
| 12 | – | – | 0,0001 | 0,0006 | 0,0034 | 0,0113 | 0,0264 | 0,0481 | 0,0728 | |
| 13 | – | – | – | 0,0002 | 0,0013 | 0,0052 | 0,0142 | 0,0296 | 0,0504 | |
| 14 | – | – | – | 0,0001 | 0,0005 | 0,0022 | 0,0071 | 0,0169 | 0,0324 | |
| 15 | – | – | – | – | 0,0002 | 0,0009 | 0,0033 | 0,0090 | 0,0194 | |
| 16 | – | – | – | – | – | 0,0003 | 0,0014 | 0,0045 | 0,0109 | |
| 17 | – | – | – | – | – | 0,0001 | 0,0006 | 0,0021 | 0,0058 | |
| 18 | – | – | – | – | – | – | 0,0002 | 0,0009 | 0,0029 | |
| 19 | – | – | – | – | – | – | 0,0001 | 0,0004 | 0,0014 | |
| 20 | – | – | – | – | – | – | – | 0,0002 | 0,0006 | |
| 21 | – | – | – | – | – | – | – | 0,0001 | 0,0003 | |
| 22 | – | – | – | – | – | – | – | – | 0,0001 | |
 2020-05-21
2020-05-21 552
552






