Отчет по практической работе №12

по дисциплине: «Искусственные нейронные сети и нечеткая логика в задачах контроля и управления»

на тему: «Работа в программных приложениях пакета Matlab»

 

 

Выполнил: студент группы 78-61

ФИО

Проверил: к.т.н., доцент кафедры АИТ

Горшкова К. Л.

 

 

Альметьевск, 2020

Цель работы:

- задачи с начальными условиями (исследование потока нефти на входе насоса при его отключении);

- задача с граничными условиями.

Задание 1. Стандартным применением модели стационарного НПДВ-решения является исследование процесса экспоненциального убывания потока жидкости во входном клапане насоса при его выключении. Найдите НПДВ - решение при , если скорость потока во входном клапане в моменты времени  определяется равенством .

Листинг программы:

function ch2ex4

global kappa beta a Cp K ga sinth Phi Ph Af G0

kappa=0.171446272015689e-8;

beta=0.213024626664637e-2;

a=0.108595374561510e+4;

Cp=0.496941623289027e+4;

K=10;

ga=9.80665;

sinth=1;

Phi=1.1e+5;

Ph=797.318;

Af=3.82760;

tD=linspace(0,1,11);

G0A=270.9*(0.8+0.2*exp(-tD));

options=odeset('Mass',@mass,'MassSingular','no','Events',@events);

zU=[];

for gi=G0A,

G0=gi;

[z,y,ze,ye,ie]=ode45(@odes,[0 5],[795.5; 255.0],options); 

zU=[zU,ze(end)];

end

plot(tD,zU,'-ok');

 

function dydz=odes(z,y)

global kappa beta a Cp K ga sinth Phi Ph Af G0

rho=y(1);

T=y(2);

dydz=[(-K*G0*abs(G0/rho)-rho*ga*sinth)

(a^2*Phi*Ph*kappa)/(Cp*Af)];

function A=mass(z,y)

global kappa beta a Cp K ga sinth Phi Ph Af G0

rho=y(1);

T=y(2);

A=zeros(2);

A(1,1)=1/(rho*kappa)-(G0/rho)^2;

A(1,2)=beta/kappa;

A(2,1)=-(a^2*beta*(T+273.15)*G0)/(Cp*rho^2);

A(2,2)=G0/rho;

 

function [value,isterminal,direction]=events(z,y)

isterminal=1;

direction=0;

rho=y(1);

T=y(2);

rhosat=-3.3*(T-290.0)+738.0;

value=rho-rhosat;

 

Рисунок 1 – Уровень жидкости zU в моменты времени tD

 

Задание 2. В демонстрационной программе batonode в качестве значений длины стержня используется 1, а массы обоих тел — 0,1. Сделайте копию этой программы и модифицируйте ее текст так, чтобы можно было определить движение палочки при новых значениях этих констант: длина L=2 и масса второго тела m₂ равна 0.5.

Листинг программы:

function baton

m1=0.1; %масса тела 1

m2=0.5; %масса тела 2

L=2; %длины стержня

g=9.81;

 

tspan=linspace(0,4,25);

y0=[0;4;2;20;-pi/2;2];

options=odeset('Mass',@mass);

 

[t,y]=ode45(@f,tspan,y0,options);

 

theta=y(1,5);

X=y(1,1);

Y=y(1,3);

xvals=[X X+L*cos(theta)];

yvals=[Y Y+L*sin(theta)];

figure;

plot(xvals,yvals,xvals(1),yvals(1),'k*',xvals(2),yvals(2),'k+')

hold on

for j=2:length(t)

theta=y(j,5);

X=y(j,1);

Y=y(j,3);

xvals=[X X+L*cos(theta)];

yvals=[Y Y+L*sin(theta)];

plot(xvals,yvals,xvals(1),yvals(1),'k+',xvals(2),yvals(2),'k*')

end

hold off

 

function dydt=f(t,y)

dydt=[y(2)

        m2*L*y(6)^2*cos(y(5))

        y(4)

        m2*L*y(6)^2*sin(y(5))-(m1+m2)*g

        y(6)

       -g*L*cos(y(5)) ];

end

 

function M=mass(t,y)

M=zeros(6,6);

M(1,1)=1;

M(2,2)=m1 + m2;

M(2,6)=-m2*L*sin(y(5));

M(3,3)=1;

M(4,4)=m1 + m2;

M(4,6)=m2*L*cos(y(5));

M(5,5)=1;

M(6,2)=-L*sin(y(5));

M(6,4)=L*cos(y(5));

M(6,6)=L^2;

end

end

 

Рисунок 2 – Свободное движение палки в вертикальной плоскости под воздействием гравитационного поля

Задание 3. Модель распределения концентраций и температур в трубчатом реакторе с рециркуляцией, представленная в виде системы ОДУ:

с неразделенными граничными условиями , .

В указанной работе показано, что при значениях параметров:

, , , , ,

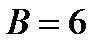начальные значения удовлетворяют (, ) ≈ (0.1, 0.6). Подтвердите этот ре­зультат и выведите график решения. В указанной работе также показано, что если значение параметра  изменить на 0.053, то при тех же значениях остальных параметров существует три решения с начальными значениями (, ), приблизительно равными (0.1, 0.7), (0.3, 1.8) и (0.44,2.6). Для получения опыта найдите все эти три решения, используя в качестве оценок компонент решения постоянные значения.

Листинг программы:

function model

betta=0;

gamma=20;

lambda=0.5;

tetta=1;

B=6;

Da=0.05;

Da=0.053;

solinit=bvpinit(linspace(0,1,10),@guess); 

sol=bvp4c(@ode,@bc,solinit,[],betta,gamma,lambda,tetta,B,
Da);

figure;

plot(sol.x,sol.y(1,:),'-*');hold on;grid on;

disp('Получаемые значения');

deval(sol,[0])

 

function v=guess(x)

v=[0.1;0.7]; %первое решение

%v=[0.3;1.8]; %второе решение

%v=[0.44;2.6]; %третье решение

end

 

function res=bc(ya,yb,betta,gamma,lambda,tetta,B,Da)

res=[ya(1)-(1-lambda)*yb(1);

   ya(2)-(1-lambda)*yb(2)];

end

 

function ode=ode(x,y,betta,gamma,lambda,tetta,B,Da)

temp=exp(gamma*y(2)/(gamma+y(2)));  

ode=[Da*(1-y(1))*temp;

B*Da*(1-y(1))*temp-betta*(y(2)-tetta)];

end

end

 

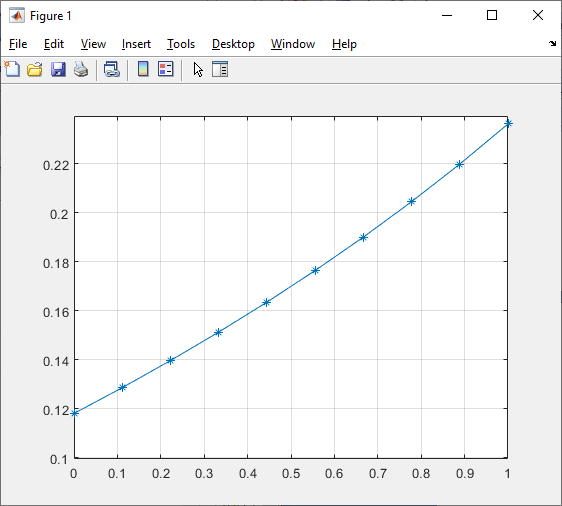
Рисунок 3 – График для первого решения

 

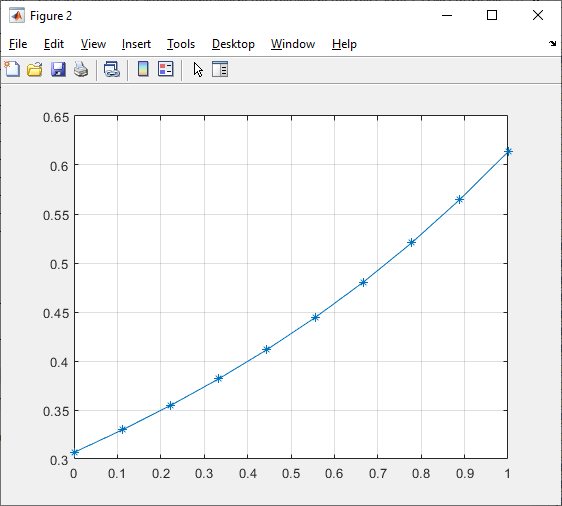
Рисунок 4 – График для второго решения

Рисунок 5 – График для третьего решения

 

Вывод: в ходе выполнения данной практической работы были выполнены задачи по исследованию потока нефти на входе насоса при его отключении и задача с граничными условиями. Результаты выполненных заданий приведены на соответствующих графиках.