СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Понятие о сложном сопротивлении
Под сложным сопротивлением (или сложным нагружением) подразумевают различные комбинации ранее рассмотренных простых нагруженных состояний брусьев (растяжение, сжатие, сдвиг, кручение или изгиб).
СЛОЖНЫЙ и КОСОЙ ИЗГИБ
 Сложным (неплоским) изгибом называется такой вид нагружения, при котором нагрузки действуют в нескольких плоскостях, проходящих через ось балки (рис.16.1, а).
Сложным (неплоским) изгибом называется такой вид нагружения, при котором нагрузки действуют в нескольких плоскостях, проходящих через ось балки (рис.16.1, а).
Рисунок1
Если нагрузки действуют в одной плоскости, не совпадающей ни с одной из главных плоскостей, то такой вид изгиба называется косым (рис.2).
 Рассмотрим косой изгиб стержня (рис.3), у которого плоскость изгиба не совпадает с главными плоскостями хz и yz
Рассмотрим косой изгиб стержня (рис.3), у которого плоскость изгиба не совпадает с главными плоскостями хz и yz
.
Рисунок 2
Изгибающий момент М (рисунок2) можно разложить на две составляющие по направлениям главных осей инерции сечения:
 (1)
(1)
где М – изгибающий момент в данном сечении в силовой плоскости р-р.
Нормальные напряжения в точке с координатами x,y можно определить суммой напряжений от  , используя принцип суперпозиции:
, используя принцип суперпозиции:
 (2)
(2)
или

 (3)
(3)
Формулы (2) и (3) позволяют определить нормальные напряжения в любой точке поперечного сечения при сложном или, как говорят ещё, пространственном изгибе. Изгибающий момент и координаты точек, в которых определяют напряжения, подставляют в формулы со своим знаком.
Уравнение нейтральной линии в сечении найдем, полагая  = 0 и обозначая координаты точек нейтральной линии (н.л.) через x0 и y0:
= 0 и обозначая координаты точек нейтральной линии (н.л.) через x0 и y0:
 (4)
(4)
Это уравнение представляет собой уравнение прямой, проходящей через начало координат (центр тяжести сечения), поскольку обращается в ноль при x0 = y0 = 0.
Положение нейтральной линии характеризуется её угловым коэффициентом
 (5)
(5)
Анализ последней формулы показывает, что:
- при косом изгибе, в отличие от плоского прямого изгиба, нейтральная линия не перпендикулярна силовой линии,
- искривление оси бруса при косом изгибе происходит в плоскости n-n, нормальной к направлению нейтральной линии (см. рис. 2, б); эта плоскость называется плоскостью изгиба,
- направление плоскости изгиба ( ) может быть перпендикулярно к плоскости действия внешней нагрузки (
) может быть перпендикулярно к плоскости действия внешней нагрузки ( ) только тогда, когда последняя совпадает с одной из главных плоскостей бруса или когда
) только тогда, когда последняя совпадает с одной из главных плоскостей бруса или когда  (круг, квадрат и т.д.);
(круг, квадрат и т.д.);  в общем случае угол наклона j нейтральной линии n-n не равен углу
в общем случае угол наклона j нейтральной линии n-n не равен углу  наклона силовой плоскости.
наклона силовой плоскости.
- Так как эпюра нормальных напряжений в сечении балки линейна, то максимальное напряжение возникает в точке, наиболее удаленной от нейтральной линии. Пусть координаты этой точки ( ). Тогда из уравнения (2) получаем:
). Тогда из уравнения (2) получаем:
- 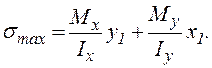 (6)
(6)
- Когда сечение симметрично относительно обеих осей, определение наибольших нагружений значительно упрощается. Так, для прямоугольного сечения легко убедиться, что максимальное напряжение будет всегда в угловых точках прямоугольника, и для них легко записать:
-
- 
- или
-  (7)
(7)
-
- При подборе сечения из условия прочности при косом изгибе
-
-  (8)
(8)
- приходится задаваться соотношением  (два неизвестных нельзя найти из одного неравенства) и путем последовательных попыток находить
(два неизвестных нельзя найти из одного неравенства) и путем последовательных попыток находить  , удовлетворяющие условию (8). В случае прямоугольного сечения
, удовлетворяющие условию (8). В случае прямоугольного сечения  . Поэтому, задаваясь соотношением
. Поэтому, задаваясь соотношением  , из условия (8) можно найти величину
, из условия (8) можно найти величину  и размеры поперечного сечения.
и размеры поперечного сечения.
ЗАДАЧА
Вычислить напряжения в угловых точках опасного сечения балки (рис. 4).
 |
 Рисунок 4
Рисунок 4
1 Разложим нагрузку по главным плоскостям:

2 Нагрузим балку соответствующей нагрузкой в вертикальной плоскости (рис.5) и построим эпюры Qх и Mу . Аналогично поступим с горизонтальной плоскостью (рис.6).
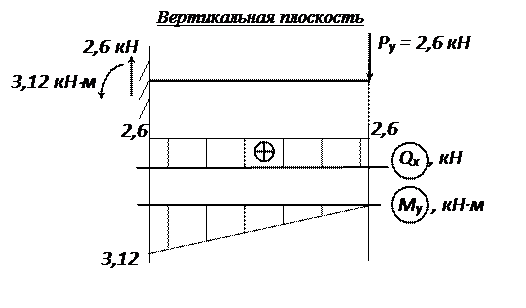 |
Рисунок 5
 Рисунок6
Рисунок6
Опасное сечение балки совпадает с сечением в заделке.
3. Расставим в угловых точках опасного сечения (7) знаки изгибающих моментов, а следовательно и напряжений, считая растягивающий момент положительным, а сжимающий – отрицательным.
 |
Рисунок 7
Найдем нормальные напряжения в угловых точках сечения:

где

Тогда 

Угол наклона нейтральной линии найдем по формуле (5):

Получаем 
Зная напряжение в точках А и С и равенство нулю  на нейтральной линии, строим эпюру
на нейтральной линии, строим эпюру  (рис.7).
(рис.7).
4 Определяем положение нейтральной  линии. Она проходит через центр тяжести сечения и через II и IV квадранты (рис. 8).
линии. Она проходит через центр тяжести сечения и через II и IV квадранты (рис. 8).
 |
Рисунок 8
Внецентренное растяжение и сжатие
Рассмотрим частный случай сложного сопротивления, когда брус растягивается (или сжимается) силами, параллельными оси бруса, так, что линия действия равнодействующей не совпадает с осью бруса (рис.9, а).
 |
Рисунок 9
Вид нагружения, при котором равнодействующая внешних сил не совпадает с осью стержня, а смещена относительно его оси и остается ей параллельна, называется внецентренным растяжением или сжатием.
Точка приложения равнодействующей Р называется полюсом силы.
Пусть точка приложения внешних сил имеет координаты хp, уp. При такой нагрузке в любом поперечном сечении бруса действуют продольная сила  и изгибающие моменты (рис. 9, б):
и изгибающие моменты (рис. 9, б):

Таким образом, внецентренное растяжение-сжатие оказывается идентичным косому изгибу. В отличие от последнего, однако, в поперечном сечении бруса возникают не только изгибающие моменты, но и продольная сила  .
.
В произвольной точке с координатами x, y нормальное напряжение s будет складываться из напряжений осевого растяжения (сжатия) силой  и напряжений от чистого изгиба моментами
и напряжений от чистого изгиба моментами 
 (9)
(9)
Очевидно, пространственная эпюра образует плоскость (поскольку входят в уравнение в первой степени), не проходящую через центр тяжести сечения (так как при 
 ).
).
Подставив в уравнения (17.1) вместо N,  ,
,  их значения, получим
их значения, получим
 .
.
Вынесем  за скобки, выразим моменты инерции через радиусы инерции (
за скобки, выразим моменты инерции через радиусы инерции (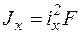 ,
,  ) и получим формулу для определения нормального напряжения в произвольной точке сечения
) и получим формулу для определения нормального напряжения в произвольной точке сечения
 . (10)
. (10)
Переменными в формулах (17.1) и (17.2) являются два последних слагаемых, отражающих влияние изгиба. Так как при изгибе наибольшие напряжения будут в точках, наиболее удаленных от нейтральной линии, то, как и при косом изгибе, надо отыскивать положение нейтральной линии.
Обозначим координаты точки, принадлежащей нейтральной линии, через x0 и y0. На нейтральной линии  , то есть
, то есть
 .
.
Так как  , то
, то  (11)
(11)
где  - координаты точки приложения равнодействующей внешних
- координаты точки приложения равнодействующей внешних
сил;
 - координаты точек на нейтральной линии.
- координаты точек на нейтральной линии.
Уравнение (11) представляет собой уравнение нейтральной линии, из которого видно, что нейтральная линия не проходит через центр тяжести сечения
Чтобы построить эту прямую, проще всего вычислить отрезки, отсекаемые ею на осях координат. Обозначим эти отрезки  и
и  (рис.10).
(рис.10).
Чтобы найти отрезок  , отсекаемый на оси Ох, надо в уравнении (11) положить
, отсекаемый на оси Ох, надо в уравнении (11) положить  ,
,  .
.
 |
Рисунок 10
Тогда получим
 .
.
Откуда  . (12)
. (12)
Аналогично, полагая  ,
,  , получим
, получим
 . (13)
. (13)
Из выражений (12) и (13) видно, что если yp и xp положительны, то отрезки  и
и  будут отрицательны, то есть нейтральная линия всегда расположена в квадранте, противоположном тому, в котором находится точка приложения внешней силы.
будут отрицательны, то есть нейтральная линия всегда расположена в квадранте, противоположном тому, в котором находится точка приложения внешней силы.
Теперь, проводя параллельно нейтральной линии касательные к контуру сечения, найдем наиболее напряженные точки А и В в растянутой и сжатой зонах сечения и построим эпюру нормальных напряжений  (рис10).
(рис10).
Напряжения в этих точках и условия прочности имеют вид
 . (14)
. (14)
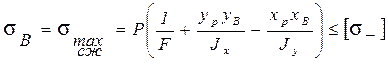 . (15)
. (15)
Для поперечных сечений с выступающими углами, у которых обе главные оси инерции являются осями симметрии (прямоугольник, двутавр и др.), координаты x, y угловых точек одновременно достигают максимальных значений. Поэтому формулы (17.6) и (17.7) можно записать в виде:
 (16)
(16)
Пример: Чугунный короткий стержень, поперечное сечение которого изображено на рис.2.5, сжимается продольной силой Р, приложенной в точке А.
Требуется:
1) Вычислить наибольшие растягивающие и наибольшие сжима-ющие напряжения в поперечном и сечении, выразив их через величину сжимающей силы Р и размеры сечения.
2) Найти допускаемую нагрузку [Р] при заданных размерах сечения и допускаемых напряжениях чугуна на сжатие [σс] и растяжение [σр].
3) Построить ядро сечения.
Дано: схема 1, а= 6см; b= 6 см; [σр]=21МПа; [σс]=110МПа
Решение
1) Определяем геометрические характеристики сечения (рис 1).

Рис. 1 Схема сечения
Сечение представляем как сложное состоящее из 3х прямоугольников. Площадь сечения
А=3∙а∙в+2∙в∙а+3∙а∙в =3∙6∙6+2∙6∙6+3∙6∙6=288 см2
Определяем положение центра тяжести всего сечения. Так как сечение симметрично относительно осей Х и У, то центр тяжести лежит в центре.
Проводим главные центральные оси.

Рисунок 1.1 Схема сечения.
Определяем осевые моменты инерции всего сечения относительно главных центральных осей фигуры по формулам:
 ,
,  .
.
Моменты инерции прямоугольника относительно собственных главных центральных осей равны
 ;
; 
 ;
; 
Расстояние между главными центральными осями х, у и собственными осями определяем по чертежу
Расстояние между главной центральной осью х и осями х1, х2, х3:
а1=в/2+в=6/2+6=9см;
а3= – в/2 – в = – 6/2 – 6= – 9см
а2=0, так как главная центральная ось х2 совпадает с главной центральной осью сечения
Расстояние между главной центральной осью у и осями у1, у2, у3равны нулю, так как главные центральные оси у1, у2, у3 совпадают с главной центральной осью сечения:

Подставив, найденные величины в формулы для вычисления главных центральных моментов инерции


Квадраты главных центральных радиусов инерции


Определяем положение нулевой линии
Нормальные напряжения при внецентренном действии продольной силы определяется по формуле

Где ХР; УР –координаты точки приложения продольной силы; х,у– координаты текущей точки поперечного сечения стержня.
По условию задачи сила Р приложена в точке А, координаты которой в системе главных центральных осей:
ХР= – (3+6)= –9см; УР=–(6+6)= –12см.
Проводим нулевую линию, для чего приравниваем выражение нормальных напряжений нулю.

 , то равным 0 может быть выражение в скобках
, то равным 0 может быть выражение в скобках

Перепишем это уравнение прямой в виде уравнения прямой в отрезках, отсекаемых на осях координат.
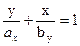
где отрезки, отсекаемые нулевой линией на осях координат


На осях координат х, у откладываем в масштабе величины найденных отрезков и проводим нулевую линию

Рис.1.2 Расчетная схема сечения.
2) Определяем допускаемую нагрузку [Р]
Вычисление максимальных нормальных напряжений в поперечном сечении бруса.
Максимальные напряжения возникают в точках наиболее удаленных от нейтральной линии. В рассматриваемой задаче это точки А и В.
В точке А с координатами ХА= – (3+6)= –9см; УА=–(6+6)= –12см.;. напряжения сжимающие, в точке В с координатами ХВ= (3+6)= 9см; УВ= (6+6)= 12см напряжения растягивающие. Координаты опасных точек находим по рисунку 1.2
Максимальные растягивающие и сжимающие напряжения выражаем через внешнюю нагрузку

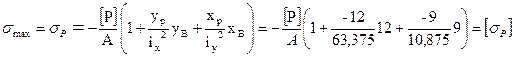
Откуда
 , где
, где



Откуда
 , где
, где

Допускаемая нагрузка [Р] из двух значений, полученных для растянутой и сжатой зон, выбираем меньшую величину [Р]=69,4кН.
 2020-06-12
2020-06-12 139
139






