Степень с рациональными и действительными показателями

Преобразование выражений, содержащих степени и корни.

Арифметический корень n -й степени и его свойства.

Арифметическим корнем натуральной степени n≥2 из неотрицательного числа a называется неотрицательное число, n -я степень которого равна a.

Арифметический корень n-ой степени из числа a обозначается так:

Число a называется подкоренным выражением. Если n=2, то вместо   пишут .

Арифметический корень второй степени называют также квадратным корнем, а корень третьей степени – кубическим корнем.

Чтобы, используя определение, доказать, что корень n -й степени   (a≥0) равен b ( , нужно показать, что: 1). b 2).

Например, , так как 4  и

Из определения арифметического корня следует, что если a , то , а также

 Например, , =13.

Действие, посредством которого отыскивается корень n-ой степени, называется извлечением корня n-ой степени. Это действие является обратным действием возведения в n-ю степень.

Решите уравнение: , .

Решите уравнение: . Число -2 называют кубическим корнем из -8.

Задание 1. Вычислить  -

 -

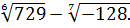
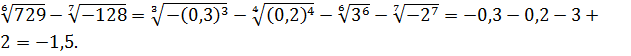
Свойства арифметического корня n-ой степени.

Арифметический корень n-ой степени обладает следующими свойствами: если a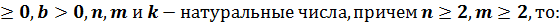

1. = .

2.

3. .

4.

5. .

6.

Примеры применения свойств арифметического корня:

Задание 2. Вычислить:

Задание 3. Упростить выражение

Используя свойства арифметического корня, получаем:

Степень с рациональными и действительными показателями.

Степень с целым отрицательным показателем определяется равенством  ,a≠0, n- натуральное число.

Степень с нулевым показателем определяется 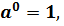где a≠0.

Степень с рациональным показателем q определяется для любого положительного основания a равенством: , где m -целое число, n - натуральное число.

Например:

;

;

;

Все свойства степени с натуральным показателем верны для степени с любым рациональным показателем и положительным основанием.

Для любых рациональных p и q  и любых a>0 и b>0 верны равенства:

1.

2.

3.

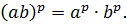
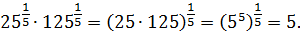
Примеры применения свойств степени:

Задание 5. Упростите выражение .

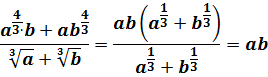
действительным числом:

Для степени с действительным показателем сохраняются все известные свойства степени с рациональным показателем.

Задание 6. Упростить выражение:

Применяя свойства степени с действительным показателем, получаем:

=