Применение графического метода
Общие рекомендации
Использование графического метода целесообразно в случае, когда по данной задаче возможно построение ее графической интерпретации при приемлемой трудоемкости.
Как правило, в задания, решаемые графическим методом, входят уравнения (или соответствующие неравенства):
1) 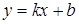 ‑ уравнение прямой;
‑ уравнение прямой;
2) 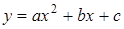 ‑ уравнение параболы;
‑ уравнение параболы;
3) 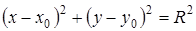 ‑ уравнение окружности с центром в точке
‑ уравнение окружности с центром в точке 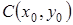 и радиусом
и радиусом  ;
;
4) 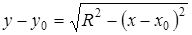 ‑ уравнение полуокружности (верхней) с центром в точке
‑ уравнение полуокружности (верхней) с центром в точке 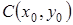 и радиусом
и радиусом  ;
;
5) уравнение с модулем;
6) уравнение, содержащее 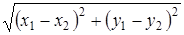 ‑ расстояние между точками
‑ расстояние между точками  и
и 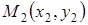 .
.
Кроме того, уравнение может иметь вид произведения, равного 0. Причем каждый из сомножителей определяет одну из вышеприведенных линий. Например, уравнение
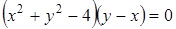
задает на плоскости объединение окружности 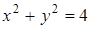 и прямой
и прямой 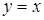 .
.
При использовании графического метода часто бывает полезным условие касания графиков двух функций 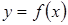 и
и 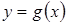 :
:
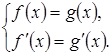
При графическом решении задач с параметрами часто бывает целесообразно использовать некоторые преобразования графиков.
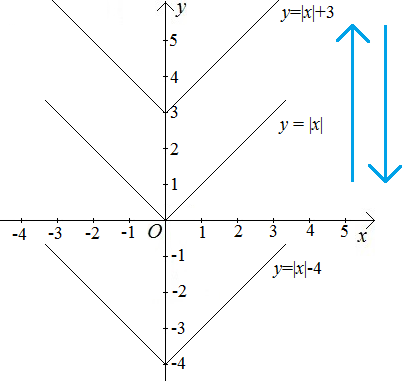
1. Пусть у нас имеется график функции 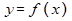 , тогда график функции
, тогда график функции 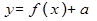 при изменении параметра
при изменении параметра  будет перемещаться вверх-вниз.
будет перемещаться вверх-вниз.
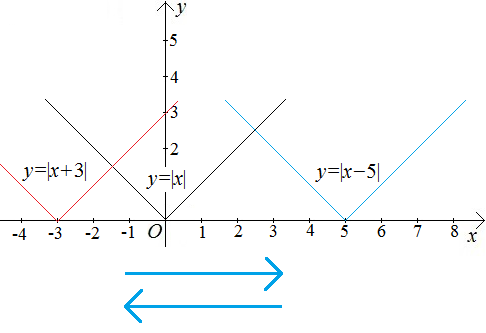
2. Пусть у нас имеется график функции 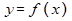 , тогда график функции
, тогда график функции 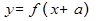 при изменении параметра
при изменении параметра  будет перемещаться вправо-влево.
будет перемещаться вправо-влево.
Если к аргументу х прибавляем положительную величину, то график движется влево, а если отрицательную, то вправо.
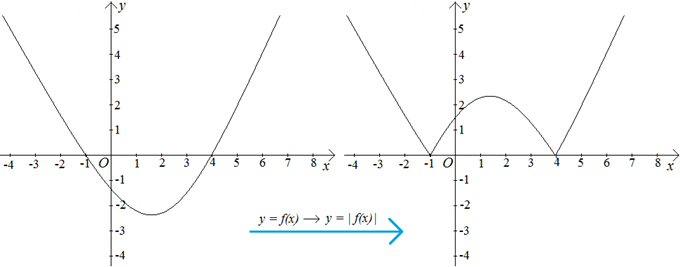
3. Если в уравнении линии переменную у заменить на ее модуль | y |, то часть линии, находящаяся в верхней полуплоскости, не изменится и отразится еще в нижнюю полуплоскость относительно оси х.
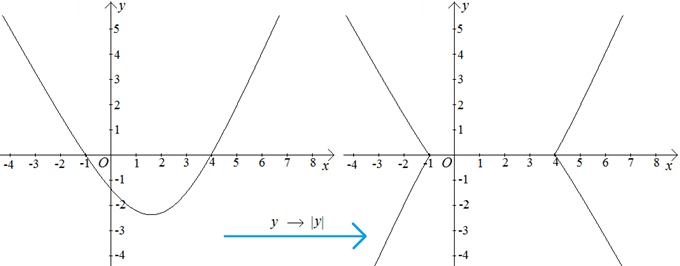
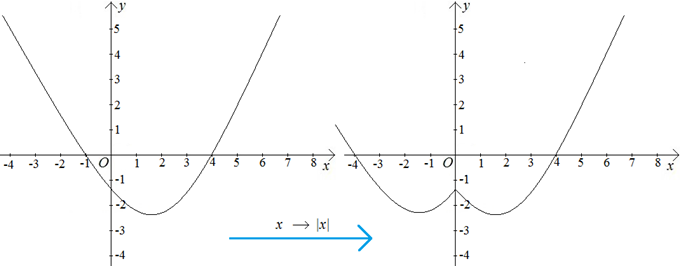
4. Если в уравнении линии переменную x заменить на ее модуль | x |, то часть линии, находящаяся в правой полуплоскости, не изменится и отразится еще в левую полуплоскость относительно оси y.
5. Если функцию 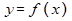 заменить на
заменить на 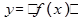 , то часть графика, находящаяся в верхней полуплоскости, не изменится, а часть графика, лежащая в нижней полуплоскости, отразится в верхнюю полуплоскость относительно оси х.
, то часть графика, находящаяся в верхней полуплоскости, не изменится, а часть графика, лежащая в нижней полуплоскости, отразится в верхнюю полуплоскость относительно оси х.
6. Если мы строим чертеж в координатах х и у, а в уравнение (неравенство) входит только одна переменная, например х, то это не значит, что мы должны построить множество точек только на оси х. В этом случае у может быть любым, поэтому каждую точку, построенную на оси х, мы должны заменить вертикальной прямой.
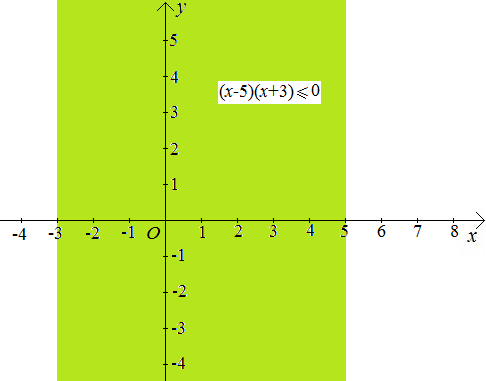
3.2.2 Построение в координатах Оху
Приведем обзор приложений построения чертежей в координатах Оху.
1. Уравнение вида 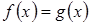 . Построим в координатах Оху графики функций
. Построим в координатах Оху графики функций 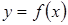 и
и 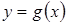 . (рисунок 12).
. (рисунок 12).
Сколько точек пересечения у построенных графиков – столько и корней у данного уравнения. В данном случае уравнение имеет два корня 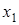 и
и 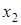 .
.
Для самостоятельного решения можно рекомендовать [6], задачи 511366, 519519, 507479, 485982 и др.
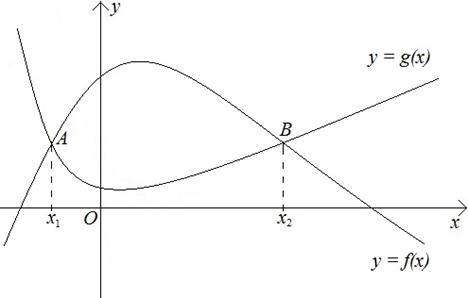
Рисунок 12
2. Неравенство вида  . Построим в координатах Оху графики функций
. Построим в координатах Оху графики функций 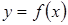 и
и 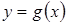 .
.
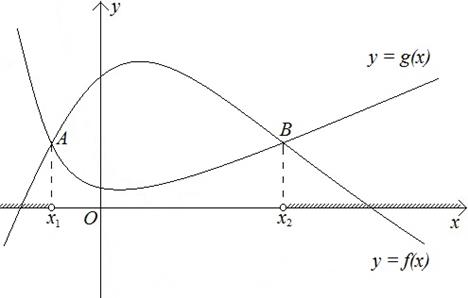
Рисунок 13
Найдем промежутки, на которых график функции 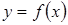 лежит ниже графика функции
лежит ниже графика функции 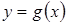 . Объединив полученные промежутки, найдем решение данного неравенства – множество
. Объединив полученные промежутки, найдем решение данного неравенства – множество 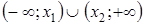 .
.
Для самостоятельного решения можно рекомендовать [6], задачи 510517, 507594, 484643 и др.
3. Система уравнений вида
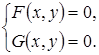
Построим в координатах Оху линии, заданные уравнениями 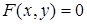 и
и 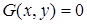 .
.
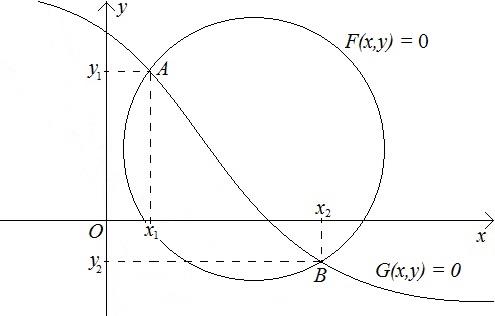
Рисунок 14
Сколько точек пересечения у построенных линий – столько система уравнений имеет решений. В данном случае система уравнений имеет два решения: 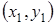 и
и 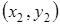 .
.
Для самостоятельного решения можно рекомендовать [6], задачи 514386, 517424, 484645, 484647, 485952 и др.
3.2.2 Построение в координатах Oxa
Приведем обзор приложений построения чертежей в координатах Оха.
1. Уравнение с параметром. Предположим, что нам удалось выразить а через х. Построим график функции 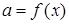 .
.
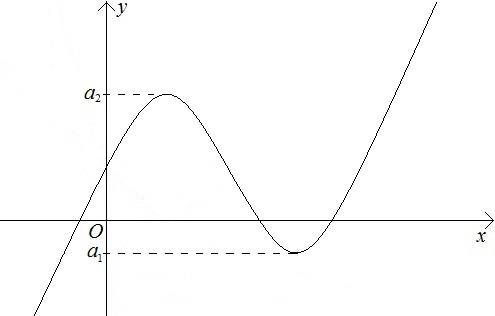
Рисунок 15
Из полученного чертежа сразу можно сделать вывод, что данное уравнение при 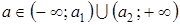 имеет один корень, при
имеет один корень, при 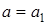 и
и 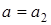 два корня, а при
два корня, а при 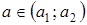 – три корня.
– три корня.
Для самостоятельного решения можно рекомендовать задачи, приведенные в статье [10].
2. Неравенство с параметром. Рассмотрим возможности применения построений в координатах Оха в данном случае на конкретных примерах.
Задача (неравенство взято из [6], задача 501219). Решите неравенство
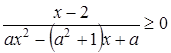
для всех положительных значений параметра а.
Решение. Разложим знаменатель на множители:
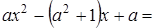
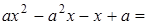
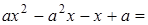
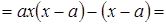
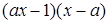 .
.
Получили неравенство
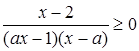 .
.
Построим в координатах 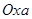 множество точек, координаты которых удовлетворяют данному неравенству.
множество точек, координаты которых удовлетворяют данному неравенству.
Замечание. Учитывая, что в задаче требуется решить неравенство при всех положительных значениях параметра, то при построении можно ограничиться только полуплоскостью 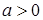 .
.
Искомое множество точек имеет следующие границы.
1. 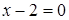 ,
, 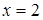 ‑ прямая. Так как неравенство нестрогое, то данная прямая будет принадлежать искомому множеству точек. Тогда построим ее сплошной линией.
‑ прямая. Так как неравенство нестрогое, то данная прямая будет принадлежать искомому множеству точек. Тогда построим ее сплошной линией.
2. 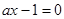 ,
, 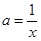 – гипербола. Так как при
– гипербола. Так как при 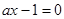 имеем деление на 0, то данная гипербола не будет принадлежать искомому множеству точек. Тогда построим гиперболу пунктирной линией.
имеем деление на 0, то данная гипербола не будет принадлежать искомому множеству точек. Тогда построим гиперболу пунктирной линией.
3.  ,
, 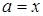 – прямая. Так как при
– прямая. Так как при  имеем деление на 0, то данная прямая не будет принадлежать искомому множеству точек. Тогда построим прямую пунктирной линией.
имеем деление на 0, то данная прямая не будет принадлежать искомому множеству точек. Тогда построим прямую пунктирной линией.
4. Так как по условию 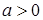 , то чертеж будет лежать в верхней полуплоскости. Отсюда следует, что прямая
, то чертеж будет лежать в верхней полуплоскости. Отсюда следует, что прямая 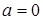 также будет границей чертежа. Так как имеем строгое неравенство, то эту прямую начертим пунктиром (рисунок 16).
также будет границей чертежа. Так как имеем строгое неравенство, то эту прямую начертим пунктиром (рисунок 16).
Построенные линии ограничивают несколько областей. Определим, какие из них принадлежат искомому множеству точек, а какие нет. Возьмем произвольную точку плоскости, не лежащую на построенных границах. Рассмотрим, например, точку 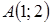 (рисунок 17).
(рисунок 17).
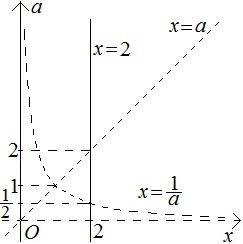
Рисунок 16
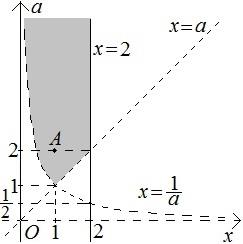
Рисунок 17
Так как при подстановке значений 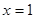 и
и 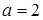 в данное неравенство, мы получим верное неравенство, то точка
в данное неравенство, мы получим верное неравенство, то точка 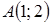 принадлежит искомому множеству точек. Построим теперь все множество точек, отвечающее решению данного неравенства, используя, что при переходе через любую границу один из множителей левой части данного неравенства будет менять знак. Отсюда следует, что любые две соседние области должны быть по-разному выделены на чертеже (рисунок 18).
принадлежит искомому множеству точек. Построим теперь все множество точек, отвечающее решению данного неравенства, используя, что при переходе через любую границу один из множителей левой части данного неравенства будет менять знак. Отсюда следует, что любые две соседние области должны быть по-разному выделены на чертеже (рисунок 18).
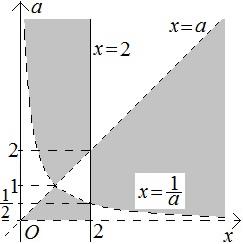
Рисунок 18
Построенное множество точек, координаты которых удовлетворяют данному неравенству, позволяет решить задачу.
Например, чтобы выяснить какое решение имеет неравенство, например, при 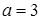 , нам достаточно найти пересечение построенного множества с горизонтальной прямой
, нам достаточно найти пересечение построенного множества с горизонтальной прямой 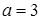 . Получим:
. Получим: 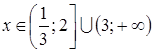 .
.
Перемещая горизонтальную прямую при 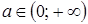 , получим ответ к данной задаче.
, получим ответ к данной задаче.
Ответ: 1) 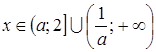 , при
, при 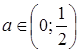 ;
;
2) 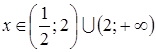 , при
, при 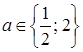 ;
;
3) 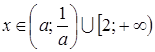 , при
, при 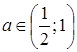 ;
;
4) 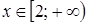 , при
, при 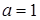 ;
;
5)  , при
, при 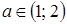 ;
;
6) 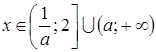 , при
, при 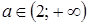 .
.
Задача ([6], задача 501219). Найти все положительные значения параметра а при каждом из которых множеством решений неравенства

является некоторый луч.
Решение. Построим в координатах 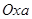 множество точек, координаты которых удовлетворяют данному неравенству (рисунок 18).
множество точек, координаты которых удовлетворяют данному неравенству (рисунок 18).
Перемещая горизонтальную прямую при 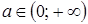 , получим, что при
, получим, что при 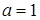 множеством решений неравенства является луч
множеством решений неравенства является луч 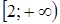 .
.
Ответ: 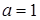 .
.
Задача. Найти все значения параметра, при которых неравенство
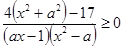
имеет хотя бы одно решение, принадлежащее отрезку  .
.
Решение. Построим в координатах 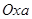 множество точек, координаты которых удовлетворяют данному неравенству.
множество точек, координаты которых удовлетворяют данному неравенству.
Теперь найдем все значения 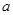 , при которых данное неравенство имеет решения, попадающие в отрезок
, при которых данное неравенство имеет решения, попадающие в отрезок 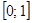 .
.
Данному отрезку в координатах 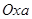 отвечает бесконечная вертикальная полоса (рисунок 20).
отвечает бесконечная вертикальная полоса (рисунок 20).
Для того чтобы определить, есть ли при данном конкретном значении 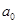 параметра
параметра 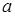 решения неравенства, попадающие в отрезок
решения неравенства, попадающие в отрезок 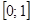 , достаточно выяснить, есть ли у горизонтальной прямой
, достаточно выяснить, есть ли у горизонтальной прямой 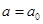 в выделенной полосе общие точки с множеством точек, отвечающим данному неравенству.
в выделенной полосе общие точки с множеством точек, отвечающим данному неравенству.
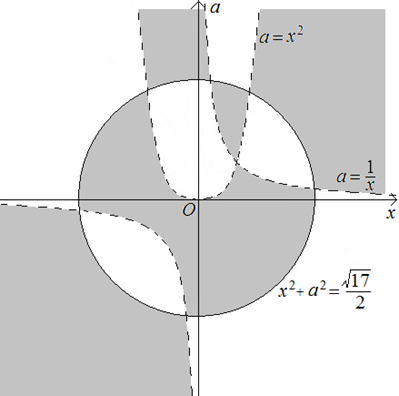
Рисунок 19
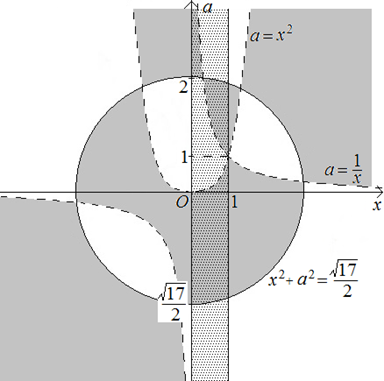
Рисунок 20
Получаем, что 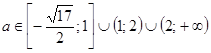 .
.
Ответ: 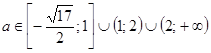 .
.
Для самостоятельного решения можно рекомендовать [6], задачи 516803 и 517267, а также статью [9].
Список использованных источников
1. Голубев, В.И. О задачах с параметрами / В.И. Голубев, А.М. Гольдман // Математика. – 2002. ‑ № 23. – С. 27-32.
2. Моргулис, А.Я. Внимание: в уравнении параметр / А.Я. Моргулис, А.Г. Мордкович, Б.А. Радунский // Квант. ‑ 1970. ‑ № 9. ‑ С. 19-25.
3. Моргулис, А.Я. Решая неравенство с параметром… / А.Я. Моргулис, А.Г. Мордкович, Б.А. Радунский // Квант. ‑ 1970. ‑ № 10. ‑ С. 51-59.
4. Вавилов, В. Задачи с параметрами / В. Вавилов // Квант. ‑ 1997. ‑ № 5. ‑ С. 38-42.
5. www.kvant.info/old.htm
6. https://ege.sdamgia.ru/
7. Горнштейн, П. Необходимые условия и задачи с параметрами / П. Горнштейн, В. Полонский, М. ЯкирА. // Квант. ‑ 1991. ‑ № 11. ‑ С. 44-49
8. Фалин, Г. Инвариантность и задачи с параметрами / Г. Фалин, А. Фалин // Квант. ‑ 2007. ‑ № 5. ‑ С. 45-47.
9. Ярский, А.С. Неравенства с параметрами / А.С. Ярский // Квант. ‑ 1987. ‑ № 3. ‑ С. 49-53.
10. Егоров, А. Решим относительно параметра / А. Егоров // Квант. ‑ 1997. ‑ № 4. ‑ С. 43-46.
11. ЕГЭ 2018. Математика. Задачи с параметром. Задача 18 (профильный уровень). Рабочая тетрадь / Под ред. Ященко И. Шестаков С.А. ‑ М.: МЦНМО, 2018. — 288 с.
ISBN: 978-5-4439-1218-9.
 2020-06-08
2020-06-08 94
94






