· Если вторая производная равна 0, то это точка перегиба.
· Если вторая производная больше 0, то на этом интервале график обладает выпуклостью вниз.
· Если вторая производная меньше 0, то на этом интервале график обладает выпуклостью вверх.
Продолжим уточнение построения графика рассматриваемой функции f(x)= 

Так как  , то
, то  3х2-4
3х2-4
 при х= -
при х= -  , х =
, х = 
Причём, при х< -  и х >
и х >  вторая производная больше 0, то есть на этих интервалах график обладает выпуклостью вниз.
вторая производная больше 0, то есть на этих интервалах график обладает выпуклостью вниз.
При -  < х <
< х <  вторая производная меньше 0, то есть на этом интервале график обладает выпуклостью вверх.
вторая производная меньше 0, то есть на этом интервале график обладает выпуклостью вверх.
· Закрепление и проверка уровня усвоения
Вариант 1
1. В чем сущность физического смысла производной/?
А. Скорость. Б. Ускорение.В. Угловой коэффициент.Г. Не знаю.
2. Точка движется по закону S(t)=2t3-3t. Чему равна скорость в момент t 0 =1с?
А. 15. Б. 12. В. 9. Г. 3.
3. Зависимость пути S от времени движения выражается формулой S=gt2/2. Назовите формулу ускорения.
А. 2gt/2. Б. 2gt. В. Gt Г. g.
4. Точка движется прямолинейно по закону S(t)=t3/3-2t2+3t+1. В какие моменты времени ее скорость будет равна 0?
А. 1 и 3. Б. 1 и 4. В. 2. Г. 2 и 0.
5. Скорость тела определяется по формуле V(t)=5t3+t2. Чему равно ускорение тела в момент времени t 0 =1с?
А. 17. Б. 32. В. 30. Г. 16.
Отыщите функцию, среди предложенных, исходя из её «автобиографии»:
Я – функция сложная, это известно,
Ещё расскажу, если Вам интересно,
Что точку разрыва и корень имею,
И есть интервал, где расти не посмею.
Во всём остальном положительна, право.
И это конечно не ради забавы.
Для чисел больших я стремлюсь к единице.
Найдите меня среди прочих в таблице.
| У=0,25х4 | У=х3-0,5х2-2х+3 | У= 
|
У= 
| У= 
| У= 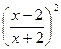
|
| У=(х2-1)2 | У=х(1-х) | У= 
|
 +3
+3  У(х) =
У(х) =  2. Тело движется по закону у =
2. Тело движется по закону у =  +
+ 
 +20. Определите скорость и ускорение в момент времени 2 с
3. Постройте график функции У(х) =
+20. Определите скорость и ускорение в момент времени 2 с
3. Постройте график функции У(х) =  - 4
- 4 
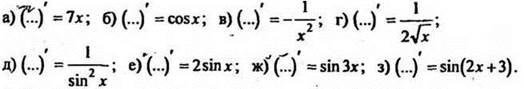 3. Являются ли первообразными для одной и той же функции следующие функции:
3. Являются ли первообразными для одной и той же функции следующие функции:
 ПРОВЕРКА ЗНАНИЙ
Вариант I
1. Докажите, что функция F есть первообразная для функции f на промежутке (-∞;∞):
ПРОВЕРКА ЗНАНИЙ
Вариант I
1. Докажите, что функция F есть первообразная для функции f на промежутке (-∞;∞):
 2. Найдите одну из первообразных для данной функции на R:
2. Найдите одну из первообразных для данной функции на R:

 Сразу разбираемся в обозначениях и терминах:
Сразу разбираемся в обозначениях и терминах:
 – значок интеграла.
– значок интеграла.
 – подынтегральная функция (пишется с буквой «ы»).
– подынтегральная функция (пишется с буквой «ы»).
 – значок дифференциала. При записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет.
– значок дифференциала. При записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет.
 – подынтегральное выражение или «начинка» интеграла.
– подынтегральное выражение или «начинка» интеграла.
 – первообразная функция.
– первообразная функция.
 – множество первообразных функций. Не нужно сильно загружаться терминами, самое важное, что в любом неопределенном интеграле к ответу приплюсовывается константа
– множество первообразных функций. Не нужно сильно загружаться терминами, самое важное, что в любом неопределенном интеграле к ответу приплюсовывается константа  .
Вычислить интеграл – это значит найти определенную функцию
.
Вычислить интеграл – это значит найти определенную функцию  , пользуясь некоторыми правилами, приемами и таблицей ИНТЕГРАЛОВ
Еще раз посмотрим на запись:
, пользуясь некоторыми правилами, приемами и таблицей ИНТЕГРАЛОВ
Еще раз посмотрим на запись:
 Посмотрим в таблицу интегралов НА ФОРЗАЦЕ УЧЕБНИКА
Что происходит? Левые части
Посмотрим в таблицу интегралов НА ФОРЗАЦЕ УЧЕБНИКА
Что происходит? Левые части  у нас превращаются в другие функции:
у нас превращаются в другие функции:  .
любой неопределенный интеграл имеет вид:
.
любой неопределенный интеграл имеет вид:  Свойства интеграла
1.Интеграл суммы равен сумме интегралов слагаемых
Свойства интеграла
1.Интеграл суммы равен сумме интегралов слагаемых
 – интеграл от алгебраической суммы двух функций равен алгебраической сумме двух интегралов от каждой функции в отдельности. Данное свойство справедливо для любого количества слагаемых.
2.Постоянный множитель можно вынести за знак интеграла
– интеграл от алгебраической суммы двух функций равен алгебраической сумме двух интегралов от каждой функции в отдельности. Данное свойство справедливо для любого количества слагаемых.
2.Постоянный множитель можно вынести за знак интеграла
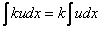 , где
, где  – постоянный множитель можно (и нужно) вынести за знак интеграла.
Решить интеграл – это значит найти множество всех первообразных, а не какую-то одну функцию.
– постоянный множитель можно (и нужно) вынести за знак интеграла.
Решить интеграл – это значит найти множество всех первообразных, а не какую-то одну функцию.
 ,
,  ,
,  ,
,  и т. д. – все эти функции являются решением интеграла
и т. д. – все эти функции являются решением интеграла 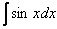 . Решений бесконечно много, поэтому записывают коротко:
. Решений бесконечно много, поэтому записывают коротко:  Пример 1
Найти интеграл. Выполнить проверку.
Пример 1
Найти интеграл. Выполнить проверку. 
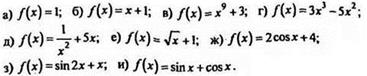 Ответы:
Ответы:

 Определение криволинейной трапеции.
2. Рассматриваем рисунки. Выясняем, какие из предложенных являются криволинейными трапециями.
Определение криволинейной трапеции.
2. Рассматриваем рисунки. Выясняем, какие из предложенных являются криволинейными трапециями.

 С помощью интеграла можно вычислять площади не только криволинейных трапеций, но и плоских фигур более сложного вида. Пусть фигура P ограничена прямыми х = a, x = b и графиками функций y = f (x) и y = g (x), причем на отрезке [ a; b ] выполняется неравенство g (x)
С помощью интеграла можно вычислять площади не только криволинейных трапеций, но и плоских фигур более сложного вида. Пусть фигура P ограничена прямыми х = a, x = b и графиками функций y = f (x) и y = g (x), причем на отрезке [ a; b ] выполняется неравенство g (x)  f (x).
Она ограничена сверху и снизу графиками функций y = f (x) и y = g (x), причем обе функции непрерывны и неотрицательны на отрезке [ a; b ].
Ее площадь можно найти как разность площадей фигур:
f (x).
Она ограничена сверху и снизу графиками функций y = f (x) и y = g (x), причем обе функции непрерывны и неотрицательны на отрезке [ a; b ].
Ее площадь можно найти как разность площадей фигур: 
 a, b – границы интегрирования (точки пересечения графиков функций y = f (x) и y = g (x))
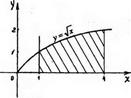
Вычислить площадь заштрихованной фигуры, изображённой на рисунке.
Вариант 1
Ответ:
a, b – границы интегрирования (точки пересечения графиков функций y = f (x) и y = g (x))
Вычислить площадь заштрихованной фигуры, изображённой на рисунке.
Вариант 1
Ответ: 
 Вариант II
Ответ: 4.
ПРОВЕРКА ЗНАНИЙ
1. Как называется функция F(x) для функции f(x)?
2. Неопределенный интеграл – это…
3. Каким действием можно проверить результат интегрирования?
4. Назовите основные методы интегрирования.
5. Криволинейная трапеция – это…
6. Как называется приращение первообразных функций F(b) –F(a) при изменении аргумента х от х=a до х=b?
7. В чем заключается геометрический смысл определенного интеграла?
8. Как вычислить площадь фигуры, ограниченной ЛИНИЯМИ
9.
9.1. Вычислите интеграл
Вариант II
Ответ: 4.
ПРОВЕРКА ЗНАНИЙ
1. Как называется функция F(x) для функции f(x)?
2. Неопределенный интеграл – это…
3. Каким действием можно проверить результат интегрирования?
4. Назовите основные методы интегрирования.
5. Криволинейная трапеция – это…
6. Как называется приращение первообразных функций F(b) –F(a) при изменении аргумента х от х=a до х=b?
7. В чем заключается геометрический смысл определенного интеграла?
8. Как вычислить площадь фигуры, ограниченной ЛИНИЯМИ
9.
9.1. Вычислите интеграл  Ответ: 1) 1; 2) -3; 3) 0; 4) 2.
9.2. Вычислите интеграл
Ответ: 1) 1; 2) -3; 3) 0; 4) 2.
9.2. Вычислите интеграл  Ответ: 1) 10/3; 2) 26/3; 3) 6; 4) 8/3.
10. Вычислите площадь фигуры, ограниченной параболой у = 1 - х2 и осью Ох. Ответ: 1) 2/3; 2) 8/3; 3) 4/3; 4) 1.
11. Вычислите площадь фигуры, ограниченной линиями y = sin2х; у = 0; х = 0 и х =
Ответ: 1) 10/3; 2) 26/3; 3) 6; 4) 8/3.
10. Вычислите площадь фигуры, ограниченной параболой у = 1 - х2 и осью Ох. Ответ: 1) 2/3; 2) 8/3; 3) 4/3; 4) 1.
11. Вычислите площадь фигуры, ограниченной линиями y = sin2х; у = 0; х = 0 и х =  /2. Ответ: 1) 2; 2) 1; 3) 1/2; 4) 3/2.
12. ЗАПИСАТЬалгоритм вычисления площади фигуры, ограниченной линиями у = х2 – 6х +11 и у = х +1. И вычислить.
Алгоритм:
1. Определяем границы плоской фигуры
2. Если границы не указаны, то находим их, решая уравнение f(x) =0 или f(x)=g(х)
3. Строим график функции / функций /
4. Запишем формулу Ньютона-Лейбница.
5. Находим первообразную функции.
6. Вычисляем значение по формуле.
Домашнее задание Вычислить площадь фигуры, ограниченной линиями:
1 вариант у = (х – 3)2 , у = 0, х = 1, х = 4.
2 вариант у = х – 2, у = х2 - 4х +2.
3 вариант у = х, у = 5 – х, х =1, х = 2
/2. Ответ: 1) 2; 2) 1; 3) 1/2; 4) 3/2.
12. ЗАПИСАТЬалгоритм вычисления площади фигуры, ограниченной линиями у = х2 – 6х +11 и у = х +1. И вычислить.
Алгоритм:
1. Определяем границы плоской фигуры
2. Если границы не указаны, то находим их, решая уравнение f(x) =0 или f(x)=g(х)
3. Строим график функции / функций /
4. Запишем формулу Ньютона-Лейбница.
5. Находим первообразную функции.
6. Вычисляем значение по формуле.
Домашнее задание Вычислить площадь фигуры, ограниченной линиями:
1 вариант у = (х – 3)2 , у = 0, х = 1, х = 4.
2 вариант у = х – 2, у = х2 - 4х +2.
3 вариант у = х, у = 5 – х, х =1, х = 2
- учебные заведения (составление расписаний)
- сфера общественного питания (составление меню)
- лингвистика (рассмотрение вариантов комбинаций букв)
- география (раскраска карт)
- спортивные соревнования (расчёт количества игр между участниками)
- производство (распределение нескольких видов работ между рабочими)
- агротехника (размещение посевов на нескольких полях) (слайд 4)
- азартные игры (подсчёт частоты выигрышей)
- химия (анализ возможных связей между химическими элементами)
- экономика (анализ вариантов купли-продажи акций) (слайд 5)
- криптография (разработка методов шифрования)
- доставка почты (рассмотрение вариантов пересылки)
 Образцы решения заданий
1.
Сколько трехзначных чисел с различными цифрами можно составить из цифр 0, 1, 2, 3, 4, 5?Р
Образцы решения заданий
1.
Сколько трехзначных чисел с различными цифрами можно составить из цифр 0, 1, 2, 3, 4, 5?Р  ешение:
И
ешение:
И  з шести данных цифр можно составить чисел, но среди них будут и трехзначные числа, начинающиеся с нуля (чего, естественно, быть не может). Посчитаем количество таких чисел. В них на первом месте стоит нуль. Значит, на оставшиеся две позиции размещают оставшиеся пять цифр. Поэтому таких чисел будет
С
з шести данных цифр можно составить чисел, но среди них будут и трехзначные числа, начинающиеся с нуля (чего, естественно, быть не может). Посчитаем количество таких чисел. В них на первом месте стоит нуль. Значит, на оставшиеся две позиции размещают оставшиеся пять цифр. Поэтому таких чисел будет
С  ледовательно, искомых чисел можно получить:
Ответ: 100.
2. Сколько существует трехзначных чисел, в которых цифры различные и нечетные.
Решение:
Н
ледовательно, искомых чисел можно получить:
Ответ: 100.
2. Сколько существует трехзначных чисел, в которых цифры различные и нечетные.
Решение:
Н  ечётных цифр пять: 1,3,5,7,9. Их надо разместить на три позиции. Поэтому количество искомых чисел равно числу размещения. Ответ: 60.
3. Найти число диагоналей n – угольника.
Решение:
И
ечётных цифр пять: 1,3,5,7,9. Их надо разместить на три позиции. Поэтому количество искомых чисел равно числу размещения. Ответ: 60.
3. Найти число диагоналей n – угольника.
Решение:
И  меем n точек плоскости, из которых никакие три не лежат на одной прямой. Соединим эти точки попарно всеми возможными способами. Будем иметь отрезков. Из этих отрезков n отрезков являются сторонами многоугольника. Тогда диагоналей будет: В соответствии с полученной формулой имеем: у треугольника 0 диагоналей, у четырехугольника 2 диагонали, у пятиугольника 5 диагоналей, у шестиугольника 9 диагоналей и т.д.
4. Сколькими способами можно составить расписание на вторник, если изучаются 10 предметов и должно быть 6 уроков (порядок уроков неважен).
Р
меем n точек плоскости, из которых никакие три не лежат на одной прямой. Соединим эти точки попарно всеми возможными способами. Будем иметь отрезков. Из этих отрезков n отрезков являются сторонами многоугольника. Тогда диагоналей будет: В соответствии с полученной формулой имеем: у треугольника 0 диагоналей, у четырехугольника 2 диагонали, у пятиугольника 5 диагоналей, у шестиугольника 9 диагоналей и т.д.
4. Сколькими способами можно составить расписание на вторник, если изучаются 10 предметов и должно быть 6 уроков (порядок уроков неважен).
Р 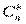 ешение:И
ешение:И  спользуем формулу для числа сочетаний из n элементов по k и получим способов. Ответ: 210.
5 Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?
Решение:
Р5 = 5!= 1 ∙2 ∙3 ∙4 ∙5 = 120 способов. Ответ:120 способов.
7. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз?
Решение:
Число всех перестановок из трех элементов равно Р3=3!, где 3!=1 · 2 · 3=6. Значит, существует шесть трехзначных чисел, составленных из цифр 1,2,3.
Ответ:6 чисел.
7.Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?
Решение:
Два юноши не могут одновременно пригласить одну и ту же девушку. И
варианты, при которых одни и те же девушки танцуют с разными юношами,
считаются разными, поэтому:
спользуем формулу для числа сочетаний из n элементов по k и получим способов. Ответ: 210.
5 Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?
Решение:
Р5 = 5!= 1 ∙2 ∙3 ∙4 ∙5 = 120 способов. Ответ:120 способов.
7. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз?
Решение:
Число всех перестановок из трех элементов равно Р3=3!, где 3!=1 · 2 · 3=6. Значит, существует шесть трехзначных чисел, составленных из цифр 1,2,3.
Ответ:6 чисел.
7.Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?
Решение:
Два юноши не могут одновременно пригласить одну и ту же девушку. И
варианты, при которых одни и те же девушки танцуют с разными юношами,
считаются разными, поэтому:
 Ответ: 360.
8. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только один раз?
Решение:
В условии задачи предложено подсчитать число всевозможных комбинаций из трех цифр, взятых из предположенных девяти цифр, причём порядок
расположения цифр в комбинации имеет значение (например, числа 132 и 231 различные). Иначе говоря, нужно найти число размещений из девяти элементов по три. По формуле числа размещений находим:
Ответ: 360.
8. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только один раз?
Решение:
В условии задачи предложено подсчитать число всевозможных комбинаций из трех цифр, взятых из предположенных девяти цифр, причём порядок
расположения цифр в комбинации имеет значение (например, числа 132 и 231 различные). Иначе говоря, нужно найти число размещений из девяти элементов по три. По формуле числа размещений находим:
 Ответ:504 трехзначных чисел.
9. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
Решение:
Чтобы рассмотреть все возможные комиссии, нужно рассмотреть все возможные 3 – элементные подмножества множества, состоящего из 7 человек. Искомое число способов равно
Ответ:504 трехзначных чисел.
9. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
Решение:
Чтобы рассмотреть все возможные комиссии, нужно рассмотреть все возможные 3 – элементные подмножества множества, состоящего из 7 человек. Искомое число способов равно
 Ответ: 35 способов.
10. В соревновании участвуют 12 команд. Сколько существует вариантов распределения призовых (1, 2, 3) мест?
Решение:
А123 = 12 ∙11 ∙10 = 1320 вариантов распределения призовых мест.
Ответ: 1320 вариантов.
11.На соревнованиях по лёгкой атлетике нашу школу представляла команда из 10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете 4´100 м на первом, втором, третьем и четвёртом этапах?
Решение:
Выбор из 10 по 4 с учётом порядка:
Ответ: 35 способов.
10. В соревновании участвуют 12 команд. Сколько существует вариантов распределения призовых (1, 2, 3) мест?
Решение:
А123 = 12 ∙11 ∙10 = 1320 вариантов распределения призовых мест.
Ответ: 1320 вариантов.
11.На соревнованиях по лёгкой атлетике нашу школу представляла команда из 10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете 4´100 м на первом, втором, третьем и четвёртом этапах?
Решение:
Выбор из 10 по 4 с учётом порядка: 
 способов.
Ответ: 5040 способов.
12. Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?
Решение:
На первое место можно поставить любой из четырех шариков (4 способа), на
второе – любой из трех оставшихся (3 способа), на третье место – любой из
оставшихся двух (2 способа), на четвертое место – оставшийся последний шар.
Всего 4 · 3 · 2 · 1 = 24 способа. Р4 = 4! = 1 · 2 · 3 · 4 = 24. Ответ: 24 способа.
13. Студентам дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами студент может выбрать из них 6 книг?
Решение:
Выбор 6 из 10 без учёта порядка:
способов.
Ответ: 5040 способов.
12. Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?
Решение:
На первое место можно поставить любой из четырех шариков (4 способа), на
второе – любой из трех оставшихся (3 способа), на третье место – любой из
оставшихся двух (2 способа), на четвертое место – оставшийся последний шар.
Всего 4 · 3 · 2 · 1 = 24 способа. Р4 = 4! = 1 · 2 · 3 · 4 = 24. Ответ: 24 способа.
13. Студентам дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами студент может выбрать из них 6 книг?
Решение:
Выбор 6 из 10 без учёта порядка:  способов.
Ответ:210 способов.
14. В группе 1М- 7 студентов, в 1МБ - 9 студентов, а в1Ф - 8 студентов. Для работы на конференции надо выбрать двух студентов из 1М, трех – 1МБ, и одного – из 1Ф. Сколько существует способов выбора студентов для работы конференции?
Решение:
Выбор из трёх совокупностей без учёта порядка, каждый вариант выбора из
первой совокупности (С72) может сочетаться с каждым вариантом выбора из
второй (С93) и с каждым вариантом выбора третьей (С81) по правилу умножения получаем:
способов.
Ответ:210 способов.
14. В группе 1М- 7 студентов, в 1МБ - 9 студентов, а в1Ф - 8 студентов. Для работы на конференции надо выбрать двух студентов из 1М, трех – 1МБ, и одного – из 1Ф. Сколько существует способов выбора студентов для работы конференции?
Решение:
Выбор из трёх совокупностей без учёта порядка, каждый вариант выбора из
первой совокупности (С72) может сочетаться с каждым вариантом выбора из
второй (С93) и с каждым вариантом выбора третьей (С81) по правилу умножения получаем:
 Ответ: 14 112 способов.
15.Студенты Женя, Сережа, Коля, Наташа и Оля побежали на перемене к теннисному столу, за которым уже шла игра. Сколькими способами подбежавшие к столу пятеро студентов могут занять очередь для игры в настольный теннис?
Решение:
Первым в очередь мог встать любой студент, вторым – любой из оставшихся троих, третьим – любой из оставшихся двоих и четвёртым – студентов, подбежавший предпоследним, а пятым – последний. По правилу умножения у пяти студентов существует 5· 4×3×2×1=120 способов занять очередь.
Ответ:120 способов.
Задания для самостоятельного решения
1. Сколькими способами читатель может выбрать две книги из пяти возможных?
Решение.
Искомое число способов равно числу сочетаний из пяти по две:
Ответ: 14 112 способов.
15.Студенты Женя, Сережа, Коля, Наташа и Оля побежали на перемене к теннисному столу, за которым уже шла игра. Сколькими способами подбежавшие к столу пятеро студентов могут занять очередь для игры в настольный теннис?
Решение:
Первым в очередь мог встать любой студент, вторым – любой из оставшихся троих, третьим – любой из оставшихся двоих и четвёртым – студентов, подбежавший предпоследним, а пятым – последний. По правилу умножения у пяти студентов существует 5· 4×3×2×1=120 способов занять очередь.
Ответ:120 способов.
Задания для самостоятельного решения
1. Сколькими способами читатель может выбрать две книги из пяти возможных?
Решение.
Искомое число способов равно числу сочетаний из пяти по две:
 .
Итак, из пяти книжек две читатель может выбрать десятью способами.
2. Сколькими способами можно выбрать четыре монеты из четырех пятирублевых монет и из четырех двухрублевых монет?
Решение.
Эта задача о числе сочетаний из двух по четыре с повторениями:
.
Итак, из пяти книжек две читатель может выбрать десятью способами.
2. Сколькими способами можно выбрать четыре монеты из четырех пятирублевых монет и из четырех двухрублевых монет?
Решение.
Эта задача о числе сочетаний из двух по четыре с повторениями:
 .
3. Вычислить:
а)
.
3. Вычислить:
а)  б)
б)  4. Найти все натуральные n, удовлетворяющие условию:
а)
4. Найти все натуральные n, удовлетворяющие условию:
а) 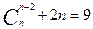 б)
б)  в)
в) 
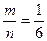 В – на втором кубике 5 очков (аналогично)
Р(В) =
В – на втором кубике 5 очков (аналогично)
Р(В) =  С- на обоих по 5 очков
Р(С)
С- на обоих по 5 очков
Р(С) 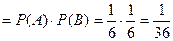 б) А - выпало одинаковое число очков
т – благоприятные исходы: 1 и 1, 2 и 2, 3 и 3, 4 и 4, 5 и 5, 6 и 6: всего 6 ожиданий
п – общее количество исходов 62 = 36
б) А - выпало одинаковое число очков
т – благоприятные исходы: 1 и 1, 2 и 2, 3 и 3, 4 и 4, 5 и 5, 6 и 6: всего 6 ожиданий
п – общее количество исходов 62 = 36
 в) А – сумма равна пяти.
т – благоприятные исходы:1 и 4, 2 и 3, 3 и 2, 4 и 1: всего 4 ожиданий
п – общее количество исходов 36
в) А – сумма равна пяти.
т – благоприятные исходы:1 и 4, 2 и 3, 3 и 2, 4 и 1: всего 4 ожиданий
п – общее количество исходов 36
 Задача 2 Вы оказались в заколдованном замке и находитесь в круглом зале с 10 дверьми, 5 из которых заперты. Вам даётся один шанс избежать колдовства: Вы должны наугад выбрать две двери, одна должна быть открыта, другая закрыта. Найдите вероятность того, что через одну дверь можно выйти, но через другую вернуться уже нельзя.
Решение:
т =
Задача 2 Вы оказались в заколдованном замке и находитесь в круглом зале с 10 дверьми, 5 из которых заперты. Вам даётся один шанс избежать колдовства: Вы должны наугад выбрать две двери, одна должна быть открыта, другая закрыта. Найдите вероятность того, что через одну дверь можно выйти, но через другую вернуться уже нельзя.
Решение:
т =  п =
п = 
 Задача 3 На каждой карточке написана одна буква. Несколько карточек наугад выкладывают одна за другой. Какова вероятность тог, что при выкладывании
а) 3 карточек получится слово Р О Т
б) 4 карточек получится слово С О Р Т
в) 5 карточек получится слово С П О Р Т
Решение:
а) А – слово РОТ
п – общее число исходов:
Задача 3 На каждой карточке написана одна буква. Несколько карточек наугад выкладывают одна за другой. Какова вероятность тог, что при выкладывании
а) 3 карточек получится слово Р О Т
б) 4 карточек получится слово С О Р Т
в) 5 карточек получится слово С П О Р Т
Решение:
а) А – слово РОТ
п – общее число исходов:  = 60
т - благоприятное число:1
= 60
т - благоприятное число:1
 б) В – слово СОРТ п - общее число исходов:
б) В – слово СОРТ п - общее число исходов:  т - благоприятное: 1
т - благоприятное: 1
 в) С- слово С П О Р Т п =
в) С- слово С П О Р Т п =  т = 1
т = 1  Задача 4 В коробке 15 неразличимых конфет, из которых 7 с шоколадной начинкой
и 8 с фруктовой. Берут наугад две конфеты. Какова вероятность того, что
а) обе конфеты с шоколадной начинкой
б) обе конфеты с фруктовой начинкой
в) одна с шоколадной, другая с фруктовой
г) хотя бы одна с шоколадной
Решение: общее число исходов: п =
Задача 4 В коробке 15 неразличимых конфет, из которых 7 с шоколадной начинкой
и 8 с фруктовой. Берут наугад две конфеты. Какова вероятность того, что
а) обе конфеты с шоколадной начинкой
б) обе конфеты с фруктовой начинкой
в) одна с шоколадной, другая с фруктовой
г) хотя бы одна с шоколадной
Решение: общее число исходов: п = 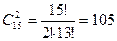 а) А – обе шоколадные
т =
а) А – обе шоколадные
т = 
 б) В – обе с фруктовой начинкой
т =
б) В – обе с фруктовой начинкой
т = 
 в) С- одна с шоколадной, другая с фруктовой
т =
в) С- одна с шоколадной, другая с фруктовой
т = 
 г) D- или обе или одна с шоколадной начинкой
т =
г) D- или обе или одна с шоколадной начинкой
т = 

 - это куб с ребром 1 см.
1
- это куб с ребром 1 см.
1  - это куб с ребром 1 м и т.д
Свойства объемов:
1. Равные тела имеют равные объемы (рис. 159 а), б) в учебнике)
2. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел (рис. 160 в учебнике).
3. Если одно тело содержит другое, то объем первого тела не меньше объема второго.
Следствие: объем куба с ребром 1/n равен 1/n3.
Теорема: Объем прямоугольного параллелепипеда равен произведению трех его измерений.
Прямоугольный параллелепипед, а, b, с - измерения, V - объем.
Доказать: V = а · b · с.
Следствие 1. Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
- это куб с ребром 1 м и т.д
Свойства объемов:
1. Равные тела имеют равные объемы (рис. 159 а), б) в учебнике)
2. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел (рис. 160 в учебнике).
3. Если одно тело содержит другое, то объем первого тела не меньше объема второго.
Следствие: объем куба с ребром 1/n равен 1/n3.
Теорема: Объем прямоугольного параллелепипеда равен произведению трех его измерений.
Прямоугольный параллелепипед, а, b, с - измерения, V - объем.
Доказать: V = а · b · с.
Следствие 1. Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
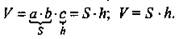 Задача № 648 а), б).
Найти объем прямоугольного параллелепипеда, стороны основания которого равны а и b, а высота равна h, если: а = 11, b = 12, h = 15;
б)
Задача № 648 а), б).
Найти объем прямоугольного параллелепипеда, стороны основания которого равны а и b, а высота равна h, если: а = 11, b = 12, h = 15;
б)  I B (а):
I B (а):  II В (б):
II В (б):  Задача № 649 б). Дано: ABCD
Задача № 649 б). Дано: ABCD  - куб, А
- куб, А  = 3√2 (рис. 1).
Найти: V.
= 3√2 (рис. 1).
Найти: V.
 Решение: Пусть ребро куба равно а, тогда
Решение: Пусть ребро куба равно а, тогда 
 (Ответ: 6√6
(Ответ: 6√6  .)
Задача № 652. Дано: ABCD
.)
Задача № 652. Дано: ABCD  - прямоугольный параллелепипед. А
- прямоугольный параллелепипед. А  = 13 см, BD = 12 см, В
= 13 см, BD = 12 см, В  = 11 см (рис. 1).
Найти: V.
= 11 см (рис. 1).
Найти: V.
 Решение: V = AD · АВ · СС1.
1) Диагональ и измерения (а, b, с) прямоугольного параллелепипеда связаны соотношением:
Решение: V = AD · АВ · СС1.
1) Диагональ и измерения (а, b, с) прямоугольного параллелепипеда связаны соотношением:  +
+  +
+ 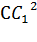 =
=  , так как
, так как  +
+  =
=  имеем, 169= 144+
имеем, 169= 144+  , C
, C  = 5 см.
2)
= 5 см.
2) 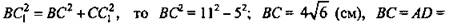
 3)
3)  Тогда
Тогда 
 (Ответ: 240√2 см3.)
Задача № 648 в), г).
в)
(Ответ: 240√2 см3.)
Задача № 648 в), г).
в)  г)
г)  (Ответ: 3,2√5.)
Объем прямой призмы равен произведению площади основания на высоту.
1. Прочитать самостоятельно доказательства следствия № 2.
2. Запись формулы объема прямой призмы, в основании которой треугольник АВС в тетради:
(Ответ: 3,2√5.)
Объем прямой призмы равен произведению площади основания на высоту.
1. Прочитать самостоятельно доказательства следствия № 2.
2. Запись формулы объема прямой призмы, в основании которой треугольник АВС в тетради:
 Задача № 653. Дано: ABCD
Задача № 653. Дано: ABCD  - прямоугольный параллелепипед, диагональ D1B = 18 составляет угол в 30° с плоскостью боковой грани, и угол в 45° с боковым ребром (рис. 6).
Найти: V.
- прямоугольный параллелепипед, диагональ D1B = 18 составляет угол в 30° с плоскостью боковой грани, и угол в 45° с боковым ребром (рис. 6).
Найти: V.
 Решение: B C1 - проекция D1B на плоскость боковой грани B B1 C1С, поэтому ∠ D1B C1= 30°, ∠ D1B B1= 45°.
1. Рассмотрим ΔD1C1B: ∠D1C1B = 90° (рис.7).
Решение: B C1 - проекция D1B на плоскость боковой грани B B1 C1С, поэтому ∠ D1B C1= 30°, ∠ D1B B1= 45°.
1. Рассмотрим ΔD1C1B: ∠D1C1B = 90° (рис.7). 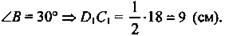
 2. Рассмотрим ΔD1B1B - прямоугольный:
2. Рассмотрим ΔD1B1B - прямоугольный:  3. Диагональ (d) и измерения (а, b, с) прямоугольного параллелепипеда связаны соотношением:
3. Диагональ (d) и измерения (а, b, с) прямоугольного параллелепипеда связаны соотношением: 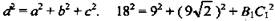

 (Ответ: V = 729√2
(Ответ: V = 729√2  Задание на дом
Задание на дом
 Решение задач (по готовым чертежам)
Дано: DABC- правильная пирамида. АВ = 3; AD = 2√3 (рис. 3).
Найти: a) Socн.; б) АО; в) DO; г) V.
Решение задач (по готовым чертежам)
Дано: DABC- правильная пирамида. АВ = 3; AD = 2√3 (рис. 3).
Найти: a) Socн.; б) АО; в) DO; г) V.
 Решение: а)
Решение: а) 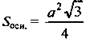 (используем формулу для вычисления площади правильного треугольника).
(используем формулу для вычисления площади правильного треугольника).  б)
б)  (формула радиуса описанной окружности через сторону правильного треугольника).
(формула радиуса описанной окружности через сторону правильного треугольника). 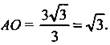 в)
в)  (по теореме Пифагора).
(по теореме Пифагора).  г)
г)  (Ответ:
(Ответ:  )
Работа с учебником. Изучение формулы объема усеченной пирамиды
)
Работа с учебником. Изучение формулы объема усеченной пирамиды
| Фигура | Формула | Обозначения |
| Куб | 
|  — ребро куба — ребро куба
|
| Призма | 
|  — площадь основания, — площадь основания,  — высота призмы — высота призмы
|
| Цилиндр | 
|  — радиус, — радиус,  — высота цилиндра — высота цилиндра
|
| Шар | 
|  — радиус — радиус
|
| Пирамида | 
|  — площадь основания, — площадь основания,  — высота пирамиды — высота пирамиды
|
| Конус | 
|  — радиус основания, — радиус основания,  — высота конуса — высота конуса
|
Задача № 704. Дано: конус, h = SO = AB = H (рис. 2).Найти: V. 
Решение: 
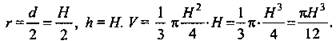 (Ответ:
(Ответ:  )
)
№ 1. Образующая конус l составляет с плоскостью основания угол α. Найдите объем конуса.
№ 2. Радиусы оснований усеченного конуса R и r; образующая наклонена к плоскости основания под углом 45°. Найдите объем конуса.
№ 3. Длина образующей конуса равна l, а длина окружности основания С. Найдите объем конуса.
Решение задач.№ 1. (рис. 9)
 ΔРАВ - осевое сечение конуса, РА = РВ = l, РО - высота,
ΔРАВ - осевое сечение конуса, РА = РВ = l, РО - высота,  Из ΔAPO (∠O = 90°):
Из ΔAPO (∠O = 90°): 

 (Ответ:
(Ответ:  )
)
№ 2. (рис. 10).
 (R > r)
(R > r)
Дополнить усеченный конус до полного и тогда  где
где 
 Из ΔAPO (∠O = 90°): ∠APO = 45°, значит, РО =AO = R. Из ΔА1PO1 (∠O = 90°): ∠A1 = 45°, значит,
Из ΔAPO (∠O = 90°): ∠APO = 45°, значит, РО =AO = R. Из ΔА1PO1 (∠O = 90°): ∠A1 = 45°, значит, 

№ 3. (рис. 12).
 ΔAPB – осевое сечение конуса.
ΔAPB – осевое сечение конуса. 
 Из ΔAPO(∠O = 90°): по теореме Пифагора
Из ΔAPO(∠O = 90°): по теореме Пифагора 

 (Ответ:
(Ответ:  )
)
- Отметим, что формула объема усеченного конуса такая же, как и формула объема усеченной пирамиды. 
Домашнее задание.
№ 1. Вычислите объем конуса, если его высота 6 см, а площадь основания 42  . (Ответ: 84
. (Ответ: 84  )
)
№ 2. Объем конуса с радиусом основания 4 м и высотой 6 м равен: (Ответ: 32π  .)
.)
№ 3. Найдите площадь основания конуса, если его объем равен 256  , а высота 4 м. (Ответ: 252
, а высота 4 м. (Ответ: 252  )
)
№ 4. Вычислите объем усеченного конуса, высота которого 3 см, а площадь оснований 16  и 4
и 4  (Ответ: 32
(Ответ: 32  )
)
№ 5. Вычислите объем усеченного конуса, если радиусы его оснований равны 3 см и 9 см, а высота 6 см. (Ответ: 234π  )
)
 Решение:
Решение: 
 DC = h, т.е.
DC = h, т.е. 
 (Ответ:
(Ответ:  )
Задача 2. Дано: цилиндр, ABCD - осевое сечение, ABCD - квадрат, АС = 8√2 см (рис. 3).
Найдите: Vцил.
)
Задача 2. Дано: цилиндр, ABCD - осевое сечение, ABCD - квадрат, АС = 8√2 см (рис. 3).
Найдите: Vцил.
 Решение: 1)
Решение: 1)  2) Рассмотрим ΔАВС - прямоугольный, так как ABCD квадрат. Пусть АВ = ВС = X см, тогда
2) Рассмотрим ΔАВС - прямоугольный, так как ABCD квадрат. Пусть АВ = ВС = X см, тогда 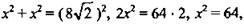
 не удовлетворяет условию задачи. Итак: АВ = ВС = 8 см, т.е. h = 8 (см).
3) Найдем радиус основания: r = 1/2AD = 4 см, тогда
не удовлетворяет условию задачи. Итак: АВ = ВС = 8 см, т.е. h = 8 (см).
3) Найдем радиус основания: r = 1/2AD = 4 см, тогда 
 4)
4)  (Ответ: 128
(Ответ: 128  )
Задача 3. Дано: цилиндр, ABCD - осевое сечение, ABCD - квадрат, АС = 6√2 см
Найдите: Vцил.
Решение:1)
)
Задача 3. Дано: цилиндр, ABCD - осевое сечение, ABCD - квадрат, АС = 6√2 см
Найдите: Vцил.
Решение:1)  2) Рассмотрим ΔАВС - прямоугольный и равнобедренный, так как ABCD - квадрат. Обозначим АВ = ВС = х см, тогда
2) Рассмотрим ΔАВС - прямоугольный и равнобедренный, так как ABCD - квадрат. Обозначим АВ = ВС = х см, тогда 
 не удовлетворяет условию задачи, т. е. АВ = ВС = 6 см, и так h = 6 см.
3) Найдем радиус основания
не удовлетворяет условию задачи, т. е. АВ = ВС = 6 см, и так h = 6 см.
3) Найдем радиус основания  4)
4)  (Ответ: 54п
(Ответ: 54п  )
Задача 4. Дано: цилиндр. (MNKL) || ОО’, ∪MAL = 120°, АО = R, ∠MKL = 30° (рис. 6).Найти: Vцил.
)
Задача 4. Дано: цилиндр. (MNKL) || ОО’, ∪MAL = 120°, АО = R, ∠MKL = 30° (рис. 6).Найти: Vцил.
 Решение:1)
Решение:1)  2) Из ΔMOL найдем ML: ∠MOL = ∪MAL = 120°. ΔMOL - равнобедренный, проведем ОА ⊥ ML. ОА ∩ ML = Н, ОН - высота, медиана и биссектриса ΔMOL.
2) Из ΔMOL найдем ML: ∠MOL = ∪MAL = 120°. ΔMOL - равнобедренный, проведем ОА ⊥ ML. ОА ∩ ML = Н, ОН - высота, медиана и биссектриса ΔMOL.  3) Высоту цилиндра находим из ΔMKL:
3) Высоту цилиндра находим из ΔMKL: 
 т. е. H = 3R.
4) Находим объем цилиндра.
т. е. H = 3R.
4) Находим объем цилиндра.  (Ответ: 3πR3.)
Объем шара
Задумывались ли вы над таким вопросом: как давно появились эти формулы, и кто первым открыл их? Еще до нашей эры формулы объемов многих тел (параллелепипеда, призмы и цилиндра) были известны. Позднее, благодаря трудам древнегреческих ученых Демокрита, Евклида и Архимеда были открыты формулы для вычисления объемов пирамиды, конуса, шара и других тел.В современных учебниках формулы для вычисления объемов пирамиды, конуса и шара выводятся на основе интегральной формулы. Но этот простой и изящный способ появился благодаря трудам И. Ноготыса и Г. Лейбница гораздо позднее того как были открыты сами формулы. Изучим и мы доказательство формулы
(Ответ: 3πR3.)
Объем шара
Задумывались ли вы над таким вопросом: как давно появились эти формулы, и кто первым открыл их? Еще до нашей эры формулы объемов многих тел (параллелепипеда, призмы и цилиндра) были известны. Позднее, благодаря трудам древнегреческих ученых Демокрита, Евклида и Архимеда были открыты формулы для вычисления объемов пирамиды, конуса, шара и других тел.В современных учебниках формулы для вычисления объемов пирамиды, конуса и шара выводятся на основе интегральной формулы. Но этот простой и изящный способ появился благодаря трудам И. Ноготыса и Г. Лейбница гораздо позднее того как были открыты сами формулы. Изучим и мы доказательство формулы  В практических приложениях часто указывается диаметр шара, поэтому в процессе решения задач полезно использовать формулу:
В практических приложениях часто указывается диаметр шара, поэтому в процессе решения задач полезно использовать формулу:  где D - диаметр шара.
Задача 5. задача № 710 в) (краткое решение).
Дано: шар, S = 64π
где D - диаметр шара.
Задача 5. задача № 710 в) (краткое решение).
Дано: шар, S = 64π  Найти: R и V.
Решение: Так как
Найти: R и V.
Решение: Так как  имеем
имеем  Тогда
Тогда  (Ответ: R = 4 см,
(Ответ: R = 4 см,  )
Задача 6. задача № 712.
Дано: Vшара = Vцил., Dшара = Dцил.
Выразить Hцил. через R.
Решение.
)
Задача 6. задача № 712.
Дано: Vшара = Vцил., Dшара = Dцил.
Выразить Hцил. через R.
Решение.  (Ответ: Н = 4/3R.)
Задача 7. Разобрать и записать в тетрадях вопрос № 9 к главе VII (стр. 161).
(Ответ:
(Ответ: Н = 4/3R.)
Задача 7. Разобрать и записать в тетрадях вопрос № 9 к главе VII (стр. 161).
(Ответ:  )
Домашнее задание
П. 71 № 710 а), б); 711; 713
1. Вычислите объем шара, если его радиус R = 6 см.
2. Вычислите диаметр шара, если его объем V = 36π.
3. В цилиндр вписан шар радиуса R = 1. Найдите отношение Vцил.: Vшара
)
Домашнее задание
П. 71 № 710 а), б); 711; 713
1. Вычислите объем шара, если его радиус R = 6 см.
2. Вычислите диаметр шара, если его объем V = 36π.
3. В цилиндр вписан шар радиуса R = 1. Найдите отношение Vцил.: Vшара
 2020-06-08
2020-06-08 202
202






