Проверочный тест по дисциплине «Математический анализ»

(Форма контроля – экзамен)

Тест по дисциплине «Математический анализ» содержит 15 вопросов на 90 минут, из них - 2 вопроса по теории и 13 задач.

Вопросы выбираются случайным образом из заданных наборов вопросов.

Тип теста: «укажите 1 верный ответ».

За каждый вопрос можно получить 0 баллов (минимум), если выбран неправильный ответ, и 1 балл (максимум), если выбран правильный ответ.

Максимальное количество баллов за тест – 15 баллов. Для успешной сдачи теста необходимо набрать не менее 8 баллов.

Количество попыток на тест – 2.

Результат теста должен выглядеть как количество набранных баллов и указание результата («тест не сдан», «тест сдан, получена оценка»).

 

Критерии оценивания:

от 0 до 7 баллов – «тест не сдан»

8-9 баллов – тест сдан, оценка «удовлетворительно»

10-12 баллов – тест сдан, оценка «хорошо»

13-15 баллов – тест сдан, оценка «отлично».

Для создания ведомости необходимо количество баллов и уровень оценки.

Тема №1. Неопределенный интеграл. Определенный интеграл.

(Теоретический вопрос)

Тема №2. Двойные и криволинейные интегралы.

(Теоретический вопрос)

Тема №3. Вычисление табличных интегралов.

2. Вычислить интеграл   

 

   

 

 

 

 

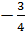
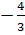
Тема №4. Вычисление интегралов на основе тождественных преобразований подынтегральной функции и использования их свойства линейности.

2.Вычислить интеграл      

*

 

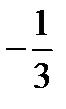
Тема №5. Вычисление интегралов на основе замены переменной.

2.Вычислить интеграл    

*

 

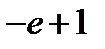
Тема №6. Вычисление интегралов на основе метода подведения под знак дифференциала.

2.Вычислить интеграл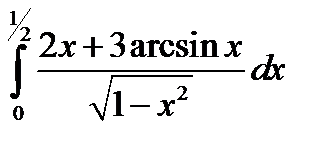               

*

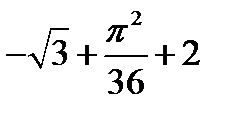
Тема №7. Вычисление интегралов методом интегрирования по частям.

2. Вычислить интеграл 

*

  

  

Тема №8. Вычисление интегралов от рациональных функций.

2. Вычислить интеграл             

*

  

  

 

 

 

Тема №9. Вычисление интегралов от тригонометрических выражений.

2.Вычислить интеграл

*

     

    

  

 

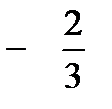
Тема №10. Вычисление интегралов от иррациональных выражений.

2. Вычислить

 

 

 

 

Тема №11. Приложения определенных интегралов (вычисление площадей плоских фигур и объемов тел вращения)

2. Вычислить площадь фигуры, ограниченной линиями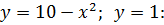  

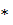36 

 9 

30 

6

Тема №12. Несобственные интегралы.

2. Вычислить несобственный интеграл    

 ;

   

   

 расходится

Тема №13. Двойные интегралы в декартовой системе координат.

2.Вычислите двойной интеграл   по области, ограниченной указанными линиями .    

-7/5

*7/5

7/6

-7/6

Тема №14. Двойные интегралы в полярной системе координат. Вычисления объемов тел с помощью двойных интегралов.

2. Вычислить повторный интеграл 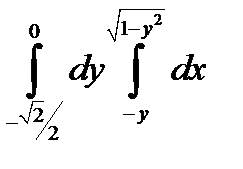  переходя к полярным координатам                           

*

 

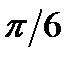
Тема №15. Криволинейные интегралы.

2. Вычислить криволинейный интеграл  вдоль линии

  ;

 

 

 

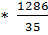
0

Таблица ответов

Номер задачи	3	4	5	6	7	8	9	10	11	12	13	14	15	Время выполнения
Номер верного ответа