Цель: рассмотреть правило параллелепипеда сложения трёх некомпланарных векторов; - научиться применять полученные знания при решении задач.
Решенные задачи писать не нужно. Они как образец для решения д/з.
1. Записать правило параллелепипеда. Рассмотреть доказательство. Зарисовать рисунок.
Для сложения компланарных векторов, так как все они лежат в одной плоскости, можно использовать правила сложения известные из планиметрии, а именно: правило треугольника, правило параллелограмма и правило многоугольника.
Что же касается некомпланарных векторов, то для построения их суммы используют правило параллелепипеда. Опишем его.
Рассмотрим некомпланарные векторы  .
.
От произвольной точки О пространства отложим векторы  ,
,  и
и  равные векторам
равные векторам  соответственно.
соответственно.
На полученных векторах можно построить параллелепипед так, чтобы они являлись его рёбрами.
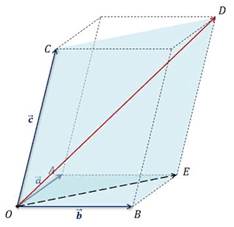
Построим вектор суммы векторов  ,
,  и
и  при этом последовательно их складывая.
при этом последовательно их складывая.
Вектором суммы векторов  ,
,  по правилу параллелограмма будет вектор
по правилу параллелограмма будет вектор 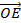 . Вектором суммы векторов
. Вектором суммы векторов 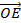 и
и  по тому же правилу будет вектор
по тому же правилу будет вектор  . Вектор
. Вектор  равен сумме векторов
равен сумме векторов  ,
,  и
и  , а значит равен сумме векторов
, а значит равен сумме векторов  .
.
Отсюда правило параллелепипеда можно сформулировать так:
Если отложить некомпланарные векторы  от некоторой точки пространства О и построить на них параллелепипед, то диагональ OD параллелепипеда будет выражать вектор суммы данных векторов.
от некоторой точки пространства О и построить на них параллелепипед, то диагональ OD параллелепипеда будет выражать вектор суммы данных векторов.
2. Воспользуемся сформулированным только что правилом и выполним задание.
№ 1. (а,в)
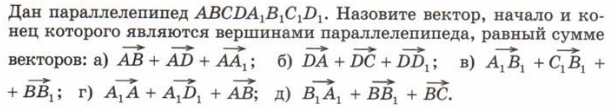
Решение:
 а) т.к. эти векторы отложены от одной точки и являются рёбрами данного параллелепипеда, то вектор их суммы будет задавать диагональ параллелепипеда, одним из концов которой будет точка начала данных векторов А. Так мы получим вектор
а) т.к. эти векторы отложены от одной точки и являются рёбрами данного параллелепипеда, то вектор их суммы будет задавать диагональ параллелепипеда, одним из концов которой будет точка начала данных векторов А. Так мы получим вектор 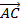 .
.
 в) В данном случае векторы не имеют общего начала, а имеют общий конец.
в) В данном случае векторы не имеют общего начала, а имеют общий конец.
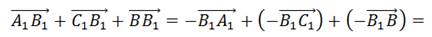 Выразим каждый из данных векторов через противоположный.
Выразим каждый из данных векторов через противоположный.

3. Домашнее задание.
№ 1 (б, г, д)
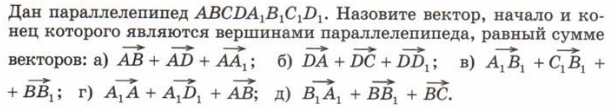
 2020-06-08
2020-06-08 1802
1802






