Замечательные пределы

Предел функции

Определение 1. Пусть функция  определена в некоторой окрестности точки a, кроме, может быть, самой точки a. Число A называется пределом функции   в точке a (или при x, стремящемся к a), если для любой последовательности допустимых значений аргумента , сходящейся к a (т.е. ), последовательность соответствующих значений функции  сходится к числу A. В этом случае пишут  или  при .

Определение 2. Назовём окрестностью точки c любой интервал , содержащий c, а  – окрестностью точки c интервал , где .

Определение 3. Число A называется пределом функции  при стремлении x к a (или в точке a), если для любого числа  существует такое число , что для всех , удовлетворяющих условию , имеет место неравенство .

 

Бесконечно большие и бесконечно малые функции

Определение 2. Функция  является бесконечно большой при , если . Функция  называется бесконечно малой при  или при , если  или .

Теорема 1. Если функция  бесконечно малая при  (или при ) и  для  из некоторой окрестности точки a, то функция  бесконечно большая при  (или при ). Верно обратное утверждение: если функция  бесконечно большая при  (или при ), то функция  бесконечно малая при  (при ).

Теорема 2. Сумма двух бесконечно малых функций есть бесконечно малая функция.

Определение 3. Если , где ,  бесконечно малые при , то  и  называются эквивалентными бесконечно малыми при  ( ~ ).

 

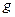Теоремы о пределах, связанные с арифметическими действиями

Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов, если последние существуют: .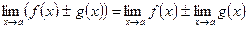

Теорема 2. Предел произведения двух функций равен произведению их пределов, если последние существуют: .

Следствие. Постоянный множитель можно выносить за знак предела:

.

Теорема 3. Предел отношения двух функций равен отношению их пределов, если последние существуют, и предел знаменателя отличен от нуля: .

Пример 1. Найдите следующие пределы:

1)

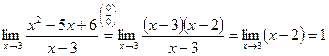
2)

 

Замечательные пределы

 

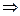
Первый замечательный предел.  ~  при .

Следствия:

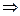
1)  ~  при        

2)  ~  при

3)  ~  при   

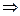
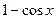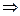
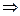
 4)  ~  при

  Второй замечательный предел.  или .

Следствия:

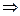
1) ~  при .

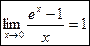
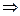
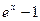2)  ~  при .

Пример 2. Найдите следующие пределы:

1)         ~  при ,  ~  при .

2)

3)             ~  при ,  ~  при .