Задание для 101 группы по алгебре за 7 мая
Тема «Формулы сложения»
1. Посмотри видео урок по теме «Формулы сложения» по ссылке videouroki.net
Теоретический материал для самостоятельного изучения
Формулы сложения - это формулы синуса суммы и разности аргументов; косинуса суммы и разности аргументов; тангенс суммы и разности аргументов.
Докажем теорему: Для любых α и β справедливо равенство
 (1)
(1)
Рассмотрим единичную окружность в прямоугольной системе координат хОу. (рис. 1)
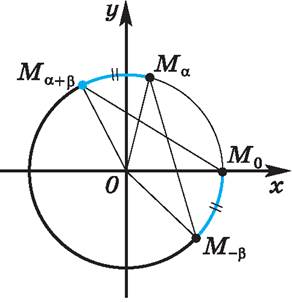
Рисунок 1 – единичная окружность
Точка  получена поворотом точки Мₒ(1;0) на угол
получена поворотом точки Мₒ(1;0) на угол 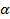 , а точка
, а точка  на угол
на угол 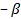 и точка
и точка  на угол
на угол  .
.
Углы  и
и 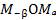 равны, отрезки
равны, отрезки  . Значит, треугольник
. Значит, треугольник  равен треугольнику
равен треугольнику  , следовательно у них одинаковые стороны
, следовательно у них одинаковые стороны  и
и 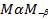 .
.
Так как синус это ордината точки на единичной окружности, а косинус её абсцисса, то точки имеют координаты
 ;
;
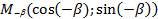 ;
;
 ).
).
Подставим координаты точек  и
и 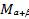 в формулу для нахождения расстояния между ними. Получим:
в формулу для нахождения расстояния между ними. Получим:

 .
.
Преобразуем левую часть, используя формулы квадрата суммы и разности двух выражений и тригонометрические тождества:

Преобразуем правую часть:

Соединим левую и правую части:

Разделим на  каждое слагаемое:
каждое слагаемое:

Получили формулу косинуса суммы.
Заменим  и учтём, что
и учтём, что  , получим формулу косинуса разности
, получим формулу косинуса разности
 (2)
(2)
Докажем, что 
Так как  ,
,  , то по формуле косинуса разности получаем:
, то по формуле косинуса разности получаем:

 Заменим
Заменим  получим
получим

Так, например,  , потому что
, потому что  .
.
Докажем, что 
Подставим в формулу  значение
значение  , получим:
, получим:


Для тангенса и котангенса тоже справедливы формулы


Выведем формулу синуса суммы и разности:
 .
.
 (3)
(3)
В этой формуле заменим  и получим формулу синуса разности:
и получим формулу синуса разности:
 (4)
(4)
Для тангенса тоже есть формула суммы и разности. По определению 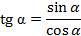 .
.
Тогда tg  , разделим числитель и знаменатель на
, разделим числитель и знаменатель на

Получаем формулу тангенса суммы  . (5)
. (5)
Заменим в ней  и учтём, что tg〖(-α)=〖-tg〗α 〗, получим формулу тангенса разности
и учтём, что tg〖(-α)=〖-tg〗α 〗, получим формулу тангенса разности
 . (6)
. (6)
Выучи формулы 1- 6
4.Рассмотри решение примеров
Пример 1. Вычислим  .
.
(Чему равен tg 450 смотрим в таблице на стр.129 учебника по алгебре)
Для котангенса суммы и разности применяют формулы:
Пример 2. Найти 
Решение: Представим  , так как нам известны значения косинуса углов
, так как нам известны значения косинуса углов 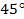 и
и  Подставим в формулу косинуса суммы. Получаем:
Подставим в формулу косинуса суммы. Получаем:
 .
.
Ответ:  .
.
Пример 3. Найти  .
.
Решение: Представим  , так как нам известны значения синуса углов
, так как нам известны значения синуса углов 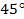 и
и 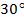 Подставим в формулу синуса суммы. Получаем:
Подставим в формулу синуса суммы. Получаем:
 .
.
Ответ:  .
.
Пример 4. Вычислите  .
.
Решение: Применяем формулу синуса разности:  .
.
Ответ: 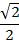
5.Изучи самостоятельно п.28 по учебнику Алгебра 10-11 автор Алимов стр.144-145.
Составь краткий конспект.
7. Реши самостоятельно задачи № 481,485(1,2)
 2020-06-08
2020-06-08 424
424






