Уточнённая схема Эйлера

Рассмотрим тот же самый пример: дифференциальное уравнение 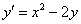, частное решение, удовлетворяющее условию 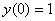, промежуток 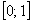и его разбиение на 10 частей
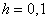( – длина каждой части).

Цель усовершенствования состоит в том, чтобы приблизить «красные квадратики» ломаной 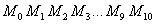к соответствующим «зелёным точкам» точного решения .

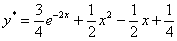И идея модификации такова: отрезки 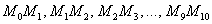должны быть параллельны касательным, которые проведены к графику функции 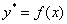не на левых краях, а «посерединке» интервалов разбиения. Что, естественно, улучшит качество приближения.

Алгоритм решения работает в том же русле, но формула, как нетрудно догадаться, усложняется:
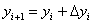, где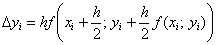

Плясать вновь начинаем от частного решения 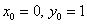и сразу же находим 1-й аргумент «внешней» функции:

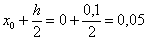
Далее следуют уже знакомые по предыдущему параграфу вычисления 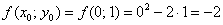, после чего можно рассчитать 2-й аргумент «внешней» функции: .

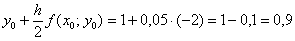Теперь находим нашего «монстра», который на поверку оказался не таким уж и страшным – обратите внимание, что это ТА ЖЕ функция 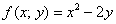, вычисленная в другой точке:

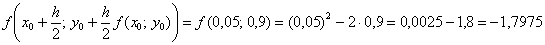
Умножаем результат на шаг разбиения:

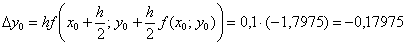
Таким образом: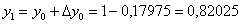

Алгоритм заходит на второй круг, не поленюсь, распишу его подробно:

рассматриваем пару 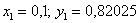и находим 1-й аргумент «внешней» функции:

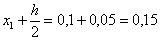
Рассчитываем 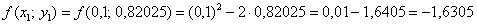и находим её 2-й аргумент: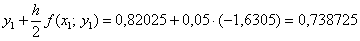

Вычислим значение:

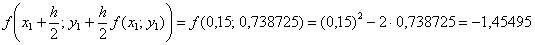
и его произведение на шаг:

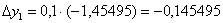
Таким образом: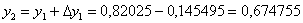

Далее рассматриваем пару 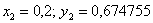и т.д.

Вычисления разумно провести в Экселе (растиражировав формулы по той же схеме – см. видеоролик выше), а результаты свести в таблицу:

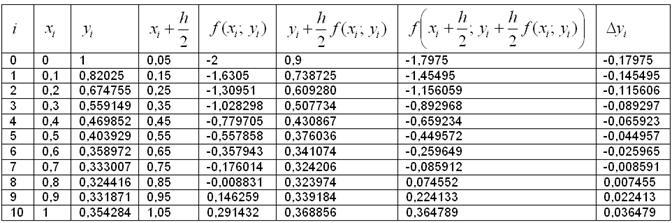
Числа целесообразно округлять до 4-5-6 знаков после запятой. Нередко в условии той или иной задачи есть прямое указание, с какой точностью следует проводить округление. Я подровнял сильно «хвостатые» значения до 6 знаков.

По результатам 2-го и 3-го столбцов (слева) построим ломаную 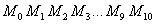, и для сравнения я снова приведу график точного решения :

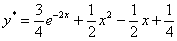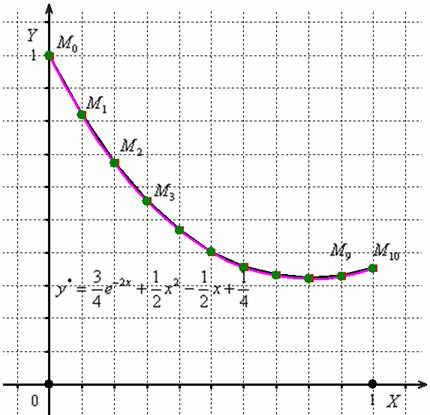
Результат существенно улучшился! – красные квадратики 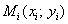практически «спрятались» за зелёными точками точного решения.