Примеры и разбор решения заданий

Рабочий лист.

Предмет	Математика
Группа	№ 14 2 курс
Тема урока	Показательные неравенства.
ФИО преподавателя	Тимиршина Алия Мунзиловна
Где находится задание:
Учебник	Колмогоров А.Н., Абрамов А.М.,Дудницын Ю.П., Ивлев Б.М., Шварцбурд С.И.. «Алгебра и начала анализа 10-11»
Ссылка	http://lib.maupfib.kg/wp-content/uploads/2015/12/Algebra_i_nachala_mat_analiz.pdf
Сроки выполнения задания
Как выполнять задание	Пишем конспект с примерами, выполняем задание и домашнее задание.
Домашняя работа	по учебнику А.Н. Колмогорова № 467
Обратная связь	Выполненные работы отправить личным сообщением ВК
Как узнать отметку о выполненном задании	Оценки будут выставлены в личный журнал преподавателя и отправлены в беседу ВК.

 

Тема: Показательные неравенства.

  Показательным называется неравенство, в котором переменная входит только в показатели степеней, при постоянном основании.

Неравенства вида , называются простейшими показательными неравенствами.

В самом простом случае неравенство принимает вид: . Очевидно, что знак неравенства может быть любым (<, >, , ).

Множество решения неравенства будет зависеть и от знака неравенства, и от основания степени, и от значения b.

Так как множество значений показательной функции 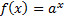– множество положительных чисел, то при 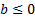неравенства: 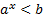и решений не имеют, независимо от значения основания а. В то же время множеством решения неравенств и является все множество действительных чисел, независимо от значения основания а (см. Рисунок 1).

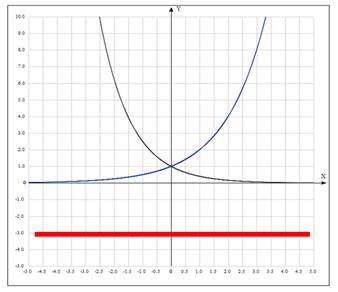рис.1

Рисунок 1 – иллюстрация решения простейшего показательного неравенства при b<0

Теперь рассмотрим случай b>0, a >1.

В том случае, когда основание степени a>1, то при переходе от исходного неравенства к неравенству с показателями знак неравенства не изменяется (см. Рисунки 2 и 3).

Рисунок 2 – иллюстрация решения простейшего показательного неравенства 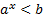или 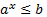при b>0, a >1.

рис.2,3

Рисунок 3 – иллюстрация решения простейшего показательного неравенства или при b>0, a >1.

Теперь рассмотрим случай b>0, 0<a<1.

В том случае, когда основание степени 0<a<1, то при переходе от исходного неравенства к неравенству с показателями знак неравенства изменяется на противоположный (см. Рисунки 4 и 5).

рис.4

Рисунок 4 – иллюстрация решения простейшего показательного неравенства 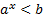или 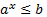при b>0, 0< a< 1.

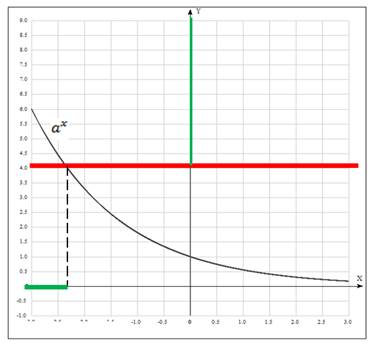рис.5

Рисунок 5 – иллюстрация решения простейшего показательного неравенства или при b>0, 0< a< 1.

Для того чтобы решить простейшее показательное неравенство , нужно число b представить в виде степени числа a.

Рассмотрим пример: .

Представим 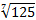в виде степени числа 5: .

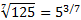Теперь перепишем данное неравенство в виде: .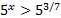

Так как основание степени больше 1, то при переходе к показателям знак неравенства сохраняется, поэтому x >3/7.

Ответ: x >3/7.

Рассмотрим еще один пример: .

Перепишем его в виде

.

Так как основание степени меньше 1, то при переходе к показателям знак неравенства изменяется на противоположный:

,

,

.

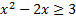Ответ:

 

2. Теперь перейдем к решению более сложных показательных неравенств.

2.1) Рассмотрим пример: .

Преобразуем показатель первого слагаемого: .

Теперь в левой части вынесем за скобку общий множитель: .

Разделим обе части неравенства на 4: 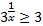. Получили простейшее показательное неравенство. Так как основание степени больше 1, то при переходе к показателям знак неравенства сохраняется, получаем: . Решение этого неравенства является полуинтервал (0; 1].

Ответ: (0; 1].

2.2) Рассмотрим еще один пример: .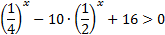

Заметим, что 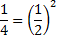, поэтому введем новую переменную . Получим вспомогательное неравенство: .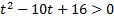

Решим его:

.

Вернемся к исходной переменной:

, .

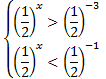Так как основание степени меньше 1, то при переходе к показателям знак неравенства изменится на противоположный:

.

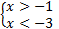Ответ: .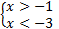

2.3) Рассмотрим еще одной показательное неравенство, которое решается методом замены переменной.

.

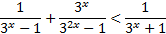Видим, что неравенство зависит от выражения , поэтому введем новую переменную 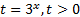и запишем вспомогательное неравенство: .

Преобразуем полученное неравенство к виду: F(t)<0.

, приведем левую часть к общему знаменателю:

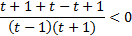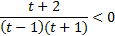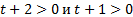, . Так как , то , поэтому решение полученного неравенства сводится к: , то есть .

Вернемся к исходной переменной: , то есть x<0.

Ответ:

Примеры и разбор решения заданий.

1. .

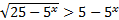Решение:

Введем новую переменную .

Запишем вспомогательное неравенство: .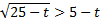

1) Если , то решением неравенства является любое значение t, которое удовлетворяет области определения: .

Решив систему: , получаем: .

2) Если (), возведем обе части неравенства в квадрат:

.

Решим его: ,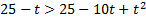

,

,

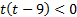0<t<9.

Учитывая условие , получаем: .

Таким образом, объединяя первый и второй случай, получаем решение иррационального вспомогательного неравенства:

.

Вернемся к исходной переменной:

. Так как всегда, то получаем: .

Учитывая, что основание степени больше 1, получаем:

Ответ: .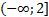

2. (x^2+x+1)^((x+5)/(x+2))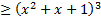

Решение:

Используем метод рационализации и перепишем неравенство в виде:

,

.

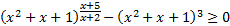Получили неравенство: .

Упростим его и решим методом интервалов:

,

.

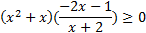Запишем ответ: .

Ответ: .

Домашнее задание: по учебнику А.Н. Колмогорова № 467