Уроки математики №92,93 Группа 1 ЖЗ 13.05.20г.
Тема: Простейшие тригонометрические уравнения
Видеоурок просмотреть на ссайте: https://yandex.fr/video/preview/?filmId=16725880822268043402&text=%3A%20урок%20математики%20110%20класс%20Простейшие%20тригонометрические%20уравнения&path=wizard&parent-reqid=1589310629056480-1671697108622801073800291-production-app-host-man-web-yp-330&redircnt=1589310683.1
Простейшие тригонометрические уравнения. Уравнение cos t = a (cos х = a).
Цель урока: ознакомиться с обратными тригонометрическими функциями, усвоение обучающимися вывода и применения формул для нахождения корней уравнения cos t = a.
Выучим определения обратных тригонометрических функций.

2. Вычислите обратные тригонометрические функции применяя таблицу значений синуса, косинуса,тангенса и котангенса (стр. 129 учебник Алгебра 10-11 класс):
1) arcsin  ; 2) arcos
; 2) arcos  ; 3) arctg
; 3) arctg  ; 4) arcsin
; 4) arcsin  ; 5) arccos
; 5) arccos  ; 6) arctg (-1);
; 6) arctg (-1);
7) arcctg (-1); 8) cos (arсcos 1); 9) sin 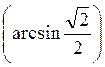 ; 10) arcsin
; 10) arcsin  ; 11) arccos
; 11) arccos  ; 12) arccos
; 12) arccos 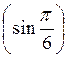 .
.
Ответы:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4) -
; 4) -  ; 5)
; 5)  ; 6) -
; 6) -  ; 7)
; 7) 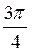 ; 8) 1; 9)
; 8) 1; 9)  ; 10)
; 10)  ; 11)
; 11)  ; 12)
; 12)  .
.
Мотивация обучения
Всем известно, что квадратные уравнения можно решать с помощью формулы их корней, что значительно упрощает работу.
В математике рассматривают уравнения, в которых неизвестное (сменная) входит только под знак тригонометрических функций, например: cos t = 1, cos t + sin t = 0. Эти уравнения называются тригонометрическими уравнениями. Как правило, решения любого тригонометрического уравнения сводится к решению простейших уравнений: sin t = a, cos t = a, tg t = a, ctg t = a.
Итак, наша задача - вывести формулы для решения простейших тригонометрических уравнений и научиться решать тригонометрические уравнения, приводимые к простейшим.

На сегодняшнем уроке рассмотрим решение уравнения cos t = a.
4. Восприятие и осознание материала по решению уравнения вида cos t = а
Таблица

ЧАСТНЫЕ СЛУЧАИ
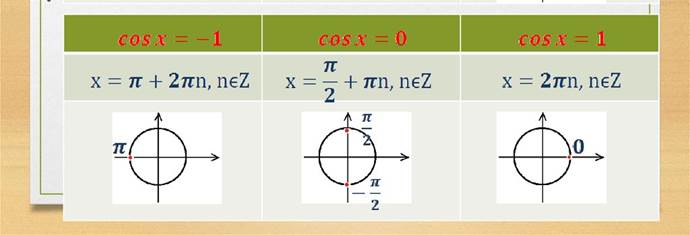
1. Если |а| > 1, то уравнение cos t = а не имеет решений, во-сколько |cos t| 1 для любого t.
2. Если |а|  1, то учитывая, что cos t - абсцисса точки Рt единичного круга, имеем: абсцису, равную а, имеют две точки (рис. 122) единичного круга (на оси ОХ отложим число а и через построенную точку проведем прямую, перпендикулярную оси абсцисс, которая пересечет окружность в двух точках
1, то учитывая, что cos t - абсцисса точки Рt единичного круга, имеем: абсцису, равную а, имеют две точки (рис. 122) единичного круга (на оси ОХ отложим число а и через построенную точку проведем прямую, перпендикулярную оси абсцисс, которая пересечет окружность в двух точках  и
и  . Тогда
. Тогда
t1 = arccos a + 2πn, n  Z,
Z,
t2 = - arccos a + 2πn, n  Z.
Z.
Эти решения можно объединить
t = ± arccos a + 2πn, n  Z (1)
Z (1)

3. Если а = 1, то, учитывая, что cos t - это абсцисса точки Рt единичного круга, имеем: абсцису, равное 1, имеет точка Рt образована из точки Р0(1; 0) поворотом на углы 2πn, n  Z. Следовательно, t = 0 + 2πn = 2πn, n
Z. Следовательно, t = 0 + 2πn = 2πn, n  Z.
Z.
4. Если а = -1, то имеем t = n + 2πn, n  Z. Корни уравнений: cos t = 1, cos t = -1, cos t = 0 можно получить из формулы t = ± arccos a + 2πn, n
Z. Корни уравнений: cos t = 1, cos t = -1, cos t = 0 можно получить из формулы t = ± arccos a + 2πn, n  Z.
Z.
Рассмотрим примеры.
Пример 1. Решите уравнение cos x =  .
.
Решение
Согласно формуле (1) имеем:
х = ± arccos  + 2πn, n
+ 2πn, n  Z.
Z.
Поскольку arccos  =
=  , то имеем: х = ±
, то имеем: х = ±  + 2πn, nєZ.
+ 2πn, nєZ.
Ответ: ±  + 2πn, n
+ 2πn, n  Z.
Z.
Пример 2. Решите уравнение cos x =  .
.
Решение
Поскольку  > 1, то уравнение корней не имеет.
> 1, то уравнение корней не имеет.
Ответ: корней нет.
Пример 3. Решите уравнение cos x = 0,37.
Решение
Согласно формуле (1) имеем:
х = arccos 0,37 + 2πn, n  Z.
Z.
Значение arccos 0,37 найдем с помощью микрокалькулятора: arccos 0,37  1,19, тогда х
1,19, тогда х  ± 1,19 + 2πn, n
± 1,19 + 2πn, n  Z.
Z.
Ответ: arccos 0,37 + 2πn  ± 1,19 + 2πn, n
± 1,19 + 2πn, n  Z.
Z.
Пример 4. Решите уравнение cos x = -  .
.
Решение
Согласно формуле (1) имеем: х = ±arccos  + 2πn, n
+ 2πn, n  Z.
Z.
Поскольку arccos  = n - arccos
= n - arccos  = n -
= n -  =
= 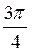 , то x = ±
, то x = ± 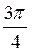 + 2πn, n
+ 2πn, n  Z.
Z.
Ответ: ± 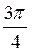 + 2πn, n
+ 2πn, n  Z.
Z.
5. Самостоятельная работа: решить №568, 571 (учебник Алгебра 10-11 класс, стр.171)
6. Домашнее задание: прочитать §33, стр. 168-171, Алгебра 10-11 класс, составить краткий конспект, рассмотреть и записать в тетрадь примеры решения задач 1,2,3,5 (стр.168-171), выполнить задания самостоятельной работы.
Выполненное задание отправлять на электронную почту: tatiefremenko@yandex.ua или страницу вКОНТАКТЕ - https://vk.com/id592773352 Индивидуальные консультации по тел.: 0660627421, 0721813966

 2020-06-10
2020-06-10 158
158






