Числовые неравенства
Данный урок посвящён теме «Свойства числовых неравенств». В ходе этого занятия вы вспомните определение неравенства. Сможете получить представление об основных свойствах числовых неравенств, которые впоследствии пригодятся для решения задач.
Что такое числовое неравенство.
Вспомним, что означают неравенства:  и
и  :
:
 означает, что
означает, что  и
и  означает, что
означает, что 
Вывод: число  считается большим числа b, если разность
считается большим числа b, если разность  является положительным числом. Число
является положительным числом. Число  считается меньше числа b, если разность
считается меньше числа b, если разность  является отрицательным числом.
является отрицательным числом.
Геометрическая интерпретация.



 Если точка с координатой
Если точка с координатой  находится правее, чем точка с координатой b, значит число
находится правее, чем точка с координатой b, значит число  . И наоборот. Не всегда очевидна алгебраическая запись, поэтому геометрическая интерпретация часто помогает. С положительными числами это очевидно, а с отрицательными лучше пользоваться расположением этих чисел на числовой оси.
. И наоборот. Не всегда очевидна алгебраическая запись, поэтому геометрическая интерпретация часто помогает. С положительными числами это очевидно, а с отрицательными лучше пользоваться расположением этих чисел на числовой оси.
Свойства числовых неравенств.
Свойство неравенств №1
Если 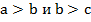 , то
, то 
Свойство неравенств №2
Если  и с – любое число, то
и с – любое число, то  .
.
Свойство неравенств №3
Если  и c – положительное число, то
и c – положительное число, то  . И если
. И если  и c – отрицательное число, то
и c – отрицательное число, то  .
.
Пример:  , умножим обе части неравенства на 2 и получим
, умножим обе части неравенства на 2 и получим  , но если обе части неравенства умножить на -2, то знак неравенства поменяется на противоположный:
, но если обе части неравенства умножить на -2, то знак неравенства поменяется на противоположный:  .
.
Выполните задания 1 – 4 из Рабочей тетради (часть 2) (п. 25, стр. 50).
Сложение и умножение числовых неравенств
Свойство 4.
 .Т. е. любые неравенства одного знака можно складывать.
.Т. е. любые неравенства одного знака можно складывать.
Свойство 5.
Рассмотрим перемножение неравенств.

Если все числа положительные, то их можно перемножить, и получим  . Если умножать на отрицательное число, то знак неравенства меняется на противоположный.
. Если умножать на отрицательное число, то знак неравенства меняется на противоположный.
Свойство 6.
Рассмотрим возведение в степень неравенств.
 и
и  тогда
тогда  .
.
Пример №1
Даны два положительных числа  и
и  .И
.И  . Доказать, что их обратные величины связаны противоположным неравенством:
. Доказать, что их обратные величины связаны противоположным неравенством: 
Решение. Перенесем в одну сторону и выполним необходимые действия. 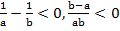
Так как даны положительные числа  и
и  то нужно убедиться, что
то нужно убедиться, что  . Чтобы дробь была отрицательным числом, надо, чтобы числитель был отрицательным числом. Умножаем
. Чтобы дробь была отрицательным числом, надо, чтобы числитель был отрицательным числом. Умножаем  на -1 и получаем
на -1 и получаем  .
.
Пример №2
Дано: 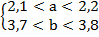
а) Оценить число 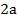
Решение: Обе части неравенства умножаем на 2. Тогда  . Задача решена.
. Задача решена.
б) Оценить число -3 
Решение:  будет меняться в пределах
будет меняться в пределах  . Умножаем неравенство на 3. Получаем
. Умножаем неравенство на 3. Получаем  ;
; 
в) Oценить разность 
Решение:  . Неравенства одного знака можно складывать. Получаем:
. Неравенства одного знака можно складывать. Получаем:

Ответ: 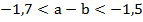
Пример №3
Дано: 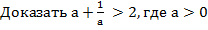
Решение: Переносим все в одну сторону.  . Приводим к общему знаменателю:
. Приводим к общему знаменателю:  Знаменатель по условию
Знаменатель по условию  , значит и числитель должен быть положительным числом, т. е.
, значит и числитель должен быть положительным числом, т. е.  . Квадрат числа всегда равен положительному числу, кроме, если а=1. Что и требовалось доказать.
. Квадрат числа всегда равен положительному числу, кроме, если а=1. Что и требовалось доказать.
Подведение итога урока.
На данном уроке была рассмотрена тема: «Свойства числовых неравенств». В ходе этого занятия вы вспомнили определение неравенства. Получили представление об основных свойствах числовых неравенств, которые впоследствии пригодятся для решения задач.
Домашнее задание
1. Сравните числа а и b, если: а)  ; б)
; б) 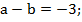 в)
в) 
2. Какое из чисел больше х или у, если известно, что: а)  ; б)
; б) 
3. №530, 532. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
 2020-06-08
2020-06-08 78
78






