2020-06-29
662Числовые последовательности. Предел последовательности
Определение 1. Бесконечной числовой последовательностью называется числовая функция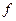 
, определённая на множестве всех натуральных чисел 
. Её обозначают 
или 
где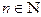 
.
Число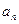 
называется n –м (общим) членом последовательности, а число n – номером члена .
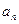Пример 1. 1) 
.
Тогда 
и т.д.
Последовательность имеет вид: 
.
2) 
.
Тогда 
, 
, 
, 
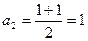и т.д.
Последовательность имеет вид: 0; 1; 0; 1; 0; 1; 
.
Последовательность, у которой все члены принимают равные между собой значения, называется постоянной последовательностью.
Определение 2. Пусть задана числовая последовательность . Число a называется пределом этой последовательности, если для каждого заданного числа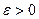 
найдётся такое натуральное число N, что для любого номера 
выполняется неравенство 
.
В этом случае пишут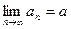 
.
Иначе,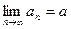 
.
Определение 3. Последовательность, имеющая предел, называется сходящейся, а не имеющая предела - расходящейся.
Бесконечно малые и бесконечно большие последовательности
Определение 4. Последовательность называется бесконечно малой, если её предел равен нулю.
Определение 5. Последовательность называется бесконечно большой, если 
.
Теорема. Если последовательность , где 
, бесконечно большая, то последовательность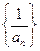 
бесконечно малая. Верно обратное утверждение: если последовательность бесконечно малая, то последовательность 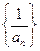бесконечно большая.
Теоремы о пределах последовательностей, связанные с арифметическими действиями
Теорема 1 (о пределе суммы). Если последовательности и 
сходятся, то их сумма 
тоже сходится и предел суммы равен сумме пределов:
.
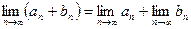Теорема 2 (о пределе произведения). Если последовательности и сходятся, то их произведение 
сходится и предел произведения равен произведению пределов:
.
Следствие 1. Постоянный множитель можно выносить за знак предела:
.
Следствие 2. Если последовательности и сходятся, то их разность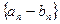 
тоже сходится и предел разности равен разности пределов:
.
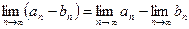Теорема 3 (о пределе частного). Если последовательности и сходятся, причём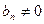 
и 
, то их частное 
тоже сходится и предел частного равен частному пределов:
.
Пример 2. Найдите следующие пределы:
1) 
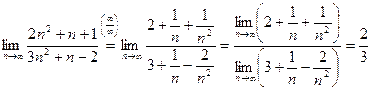
2) 
Задачи.
1. Записать последовательности:
1) 
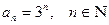
2) 
3) 
4) 
5) 
2. Найдите пределы:
1) 
2) 
3) 
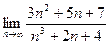
4) 
5) 
6) 
7) 
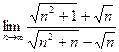
8) 
9) 
10) 
11) 
