ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ
ПЛАН ЛЕКЦИИ
I. Скалярное поле. Поверхности уровня. Градиент.
II. Векторное поле. Векторные линии.
III. Дивергенция и ротор векторного поля.
IV. Оператор Гамильтона и векторные дифференциальные операции второго порядка.
V. Свойства простейших векторных полей.
I. Скалярное поле. Поверхности уровня. Градиент. Пусть в каждой точке  области D задано значение некоторой скалярной физической величины, т.е. величины, характеризующейся только своим числовым значением. Такую величину называют скалярной функцией точки u (P) и говорят, что в области D задано скалярное поле u (P) или
области D задано значение некоторой скалярной физической величины, т.е. величины, характеризующейся только своим числовым значением. Такую величину называют скалярной функцией точки u (P) и говорят, что в области D задано скалярное поле u (P) или  .
.
Примерами скалярных полей являются: температурное поле в неравномерно нагретом теле, плотность распределения электрических зарядов в наэлектризованном изолированном теле и т.д.
Скалярное поле называют стационарным, если величина u (P) не зависит от времени t, и нестационарным, когда u (P, t).
Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция  принимает постоянное значение, т.е.
принимает постоянное значение, т.е.
 .
.
В физике такие поверхности называют эквипотенциальными поверхностями.
Если скалярное поле плоское, то геометрическое место точек, координаты которых удовлетворяют уравнению  , называют линиями уровня функции
, называют линиями уровня функции 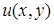 (изотермы, изобары).
(изотермы, изобары).
 Важной характеристикой скалярного поля является скорость изменения поля в заданном направлении, которая определяется как производная функции по направлению луча λ:
Важной характеристикой скалярного поля является скорость изменения поля в заданном направлении, которая определяется как производная функции по направлению луча λ:
 ,
,
 .
.
Здесь  – направляющие косинусы луча λ. Вектор, проекциями которого служат значения частных производных от функции
– направляющие косинусы луча λ. Вектор, проекциями которого служат значения частных производных от функции  , называют градиентом функции и обозначают
, называют градиентом функции и обозначают
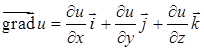 .
.
Тогда производную по направлению можно представить как скалярное произведение градиента функции на единичный вектор 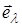 этого направления
этого направления

|
 на направление луча
на направление луча  .
.
Модуль вектора 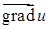 равен наибольшему возможному значению производной
равен наибольшему возможному значению производной  , а направление этого вектора характеризует направление
, а направление этого вектора характеризует направление
|
|
 совпадает с направлением нормали к поверхности уровня, проходящей через данную точку.
совпадает с направлением нормали к поверхности уровня, проходящей через данную точку.
II. Векторное поле. Векторные линии. Если в каждой точке  области D задан определенный вектор
области D задан определенный вектор  , то будем говорить, что в этой области задано векторное поле.
, то будем говорить, что в этой области задано векторное поле.
Примеры векторных полей: силовое поле, поле скоростей текущей жидкости, электромагнитное поле и т.д.
Будем рассматривать стационарные векторные поля, в которых вектор  не зависит от времени. Обозначим проекции вектора
не зависит от времени. Обозначим проекции вектора  на оси координат через
на оси координат через  , тогда
, тогда
 .
.
Предполагаем, что  – непрерывные дифференцируемые функции координат.
– непрерывные дифференцируемые функции координат.
 Векторной линией векторного поля называется линия, в каждой точке которой направление касательной совпадает с
Векторной линией векторного поля называется линия, в каждой точке которой направление касательной совпадает с  направлением вектора
направлением вектора  .
.



 Примеры векторных линий – линии тока в гидродинамике, силовые линии в физике.
Примеры векторных линий – линии тока в гидродинамике, силовые линии в физике.
Система дифференциальных уравнений семейства векторных линий поля  имеет вид
имеет вид
 .
.
Эта система представляет собой условие параллельности вектора касательной к линии 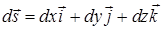 и вектора
и вектора  .
.
III. Дивергенция и ротор векторного поля. Возьмем в векторном поле

некоторую поверхность S и выберем на ней определенную сторону. Нормаль к поверхности в произвольной точке задана направляющими косинусами  .
.
Определение. Потоком вектора  через поверхность S называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности:
через поверхность S называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности:
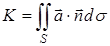 .
.
Пример. Найти поток радиус-вектора  через боковую поверхность S 1, верхнее основание S 2 и нижнее основание S 3 прямого цилиндра радиуса R и высоты H в направлении внешней нормали.
через боковую поверхность S 1, верхнее основание S 2 и нижнее основание S 3 прямого цилиндра радиуса R и высоты H в направлении внешней нормали.
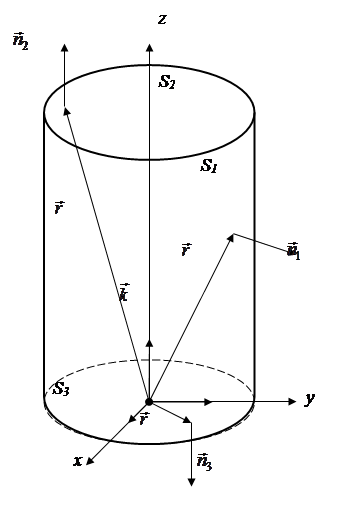 Решение. Найдем потоки вектора
Решение. Найдем потоки вектора  через поверхности S 1, S 2 и S 3, вычисляя скалярные произведения этого вектора на векторы единичных нормалей к этим поверхностям:
через поверхности S 1, S 2 и S 3, вычисляя скалярные произведения этого вектора на векторы единичных нормалей к этим поверхностям:
1) S 1:  ,
,
 ,
,
2) 

 S 2 :
S 2 :  ,
,  ,
,
 ,
,
3) S 3:  ,
, 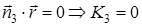 .
.
Поток вектора через полную поверхность цилиндра
|
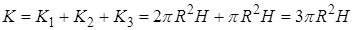 .
.
Если поверхность S замкнута и ограничивает некоторую пространственную область V, то в случае, когда берется внешняя нормаль, говорят о потоке изнутри поверхности S:
 .
.
Рассмотрим некоторую точку  векторного поля
векторного поля  и окружим ее замкнутой поверхностью S, целиком содержащейся в поле.
и окружим ее замкнутой поверхностью S, целиком содержащейся в поле.
Определение. Предел отношения потока вектора  через замкнутую поверхность S к объему V, ограниченному этой поверхностью, при условии, что вся поверхность стягивается в точку P, называется дивергенцией, или расходимостью, векторного поля:
через замкнутую поверхность S к объему V, ограниченному этой поверхностью, при условии, что вся поверхность стягивается в точку P, называется дивергенцией, или расходимостью, векторного поля:
 .
.
Дивергенция характеризует мощность источника или стока поля в точке Р и является скалярной величиной.
По формуле Остроградского
 .
.
Тройной интеграл в правой части представим с помощью теоремы о среднем:
 , где
, где  .
.
Если область V стягивается в точку Р, то Р 1→ Р и

Таким образом, дивергенция векторного поля выражается формулой
 .
.
Пользуясь этим выражением, запишем теорему Остроградского в векторной форме:
 ,
,
то есть поток вектора изнутри замкнутой поверхности S равен тройному интегралу от дивергенции поля по объему, ограниченному этой поверхностью.
В поле текущей жидкости поток жидкости через поверхность равен суммарной мощности источников и стоков, расположенных внутри этой поверхности.
Возьмем в векторном поле

некоторую замкнутую линию L и выберем на ней определенное направление. Обозначим через  вектор, имеющий направление касательной к линии и по модулю равный дифференциалу длины дуги:
вектор, имеющий направление касательной к линии и по модулю равный дифференциалу длины дуги:
 .
.
Определение. Циркуляцией вектора  вдоль замкнутого контура L называется криволинейный интеграл по этому контуру от скалярного произведения вектора
вдоль замкнутого контура L называется криволинейный интеграл по этому контуру от скалярного произведения вектора  на вектор
на вектор  касательной к контуру
касательной к контуру
 .
.
|
Если  – поле скоростей текущей жидкости, то физический смысл циркуляции можно пояснить следующим примером. Пусть L – окружность, расположенная в некоторой плоскости, которую будем рассматривать как периферию колесика с радиальными лопатками, которое может вращаться относительно оси, перпендикулярной его плоскости. Если Г =0, то колесико в таком потоке остается неподвижным. Если Г ≠0, то колесико будет вращаться тем быстрее, чем больше величина циркуляции. Таким образом, циркуляция характеризует вращательные свойства векторного поля.
– поле скоростей текущей жидкости, то физический смысл циркуляции можно пояснить следующим примером. Пусть L – окружность, расположенная в некоторой плоскости, которую будем рассматривать как периферию колесика с радиальными лопатками, которое может вращаться относительно оси, перпендикулярной его плоскости. Если Г =0, то колесико в таком потоке остается неподвижным. Если Г ≠0, то колесико будет вращаться тем быстрее, чем больше величина циркуляции. Таким образом, циркуляция характеризует вращательные свойства векторного поля.
Рассмотрим точку 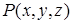 векторного поля
векторного поля  , окружим ее плоским контуром L, ограничивающим область S. Вращательные свойства поля в точке будем характеризовать пределом отношения циркуляции
, окружим ее плоским контуром L, ограничивающим область S. Вращательные свойства поля в точке будем характеризовать пределом отношения циркуляции  по контуру L к площади S, когда контур стягивается в точку Р,
по контуру L к площади S, когда контур стягивается в точку Р,
 .
.
С помощью теоремы Стокса найдем

 .
.
Последний интеграл можно вычислить по теореме о среднем в точке Р 1, которая стремится к Р при стягивании контура L в точку. Тогда
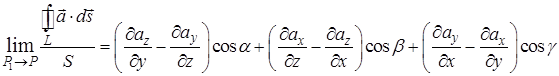 .
.
Определение. Ротором (вихрем) векторного поля называется вектор
 .
.
Проекция этого вектора на любое направление  дает
дает  . Этот предел будет наибольшим, если направление нормали
. Этот предел будет наибольшим, если направление нормали  совпадает с направлением вектора
совпадает с направлением вектора  .
.
С помощью определения ротора можно записать теорему Стокса в векторной форме:
 ,
,
то есть поток ротора поля через поверхность S равен циркуляции вектора по границе этой поверхности.
IV. Оператор Гамильтона и векторные дифференциальные операции второго порядка. Английским математиком У.Гамильтоном введен в употребление символический вектор
 ,
,
который называют набла-оператором Гамильтона. Перечислим правила действий с этим вектором:
1) произведение набла-оператора на скалярную функцию u (P) дает градиент этой функции:
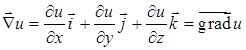 ,
,
2) скалярное произведение набла-оператора на векторную функцию  дает дивергенцию этой функции
дает дивергенцию этой функции

 .
.
3) векторное произведение набла-оператора на векторную функцию  дает ротор этой функции
дает ротор этой функции
 .
.
Действия взятия градиента, дивергенции, ротора являются дифференциальными операциями первого порядка.
Пример. Рассмотрим электрическое поле точечного заряда е, помещенного в начало координат. Оно описывается в точке  вектором напряженности
вектором напряженности  , где
, где  ,
,  .
.
Потенциалом электрического поля точечного заряда е называется функция
 .
.
Найдем градиент функции u
 .
.
Тогда напряженность электрического поля  .
.
Поверхности уровня потенциала  называют эквипотенциальными поверхностями. Они представляют собой сферы с центром в начале координат. Векторные линии поля
называют эквипотенциальными поверхностями. Они представляют собой сферы с центром в начале координат. Векторные линии поля  в каждой точке поля ортогональны проходящей через эту точку эквипотенциальной поверхности, т.е. направлены вдоль радиусов сферы.
в каждой точке поля ортогональны проходящей через эту точку эквипотенциальной поверхности, т.е. направлены вдоль радиусов сферы.
Найдем дивергенцию электрического поля

 ,
,
так как  .
.
Этот результат получен при 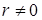 . Он означает, что в любой точке, за исключением начала координат, отсутствуют источники поля. В начале координат
. Он означает, что в любой точке, за исключением начала координат, отсутствуют источники поля. В начале координат  (бесконечная плотность заряда). Найдем ротор электрического поля
(бесконечная плотность заряда). Найдем ротор электрического поля
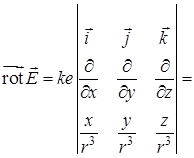
 .
.
Таким образом,  (такое поле потенциально) и, следовательно, магнитная индукция в этом поле не изменяется.
(такое поле потенциально) и, следовательно, магнитная индукция в этом поле не изменяется.
Правила вычислений с оператором Гамильтона:
1) если оператор воздействует на линейную комбинацию функций 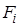 , то
, то
 ;
;
2) воздействие оператора на произведение нескольких функций выражается формулой
 .
.
Найдем, например,

С помощью набла-оператора можно записать формулу для вычисления производной скалярного поля по направлению:
 ,
,
тогда символ  называют оператором производной по направлению. Производная по направлению векторного поля равна
называют оператором производной по направлению. Производная по направлению векторного поля равна  .
.
Пусть имеется скалярное поле u (P) и градиент этого поля  . Поле градиента является векторным полем, поэтому можно искать его дивергенцию и ротор.
. Поле градиента является векторным полем, поэтому можно искать его дивергенцию и ротор.
Если задано векторное поле  , то оно порождает два поля: скалярное поле
, то оно порождает два поля: скалярное поле  и векторное поле
и векторное поле  . Тогда можно искать градиент первого поля, а также дивергенцию и ротор второго поля:
. Тогда можно искать градиент первого поля, а также дивергенцию и ротор второго поля:
1) 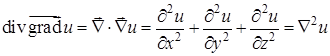 ,
,
где  - оператор Лапласа;
- оператор Лапласа;
2)  ;
;
3)  ;
;
4) 


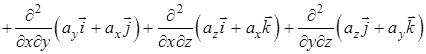
5)  ,
,
где  ;
;

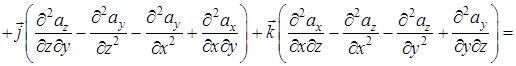

 .
.
V. Свойства простейших векторных полей.
Определение. Трубчатое (соленоидальное) поле – это векторное поле  , дивергенция которого во всех точках равна нулю:
, дивергенция которого во всех точках равна нулю:  .
.
Возьмем в этом поле какую-нибудь площадку S 0 и проведем через каждую точку ее границы векторные линии. Эти линии ограничивают часть пространства, называемую векторной трубкой. Жидкость при своем течении все время движется по своей трубке, не пересекая ее стенок.
Определим по теореме  Остроградского поток жидкости через поверхность трубки, ограниченную двумя ее сечениями S 0 и S 1:
Остроградского поток жидкости через поверхность трубки, ограниченную двумя ее сечениями S 0 и S 1:
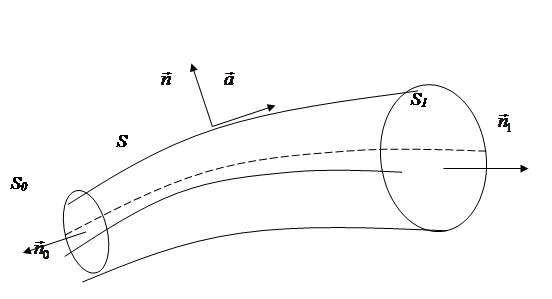 |
 .
.
Тогда  , так как нормали внешние, т.е. поток вектора в направлении векторных линий через каждое сечение векторной трубки не меняется, т.е. в поле без источников через каждое сечение трубки тока протекает одно и то же количество жидкости.
, так как нормали внешние, т.е. поток вектора в направлении векторных линий через каждое сечение векторной трубки не меняется, т.е. в поле без источников через каждое сечение трубки тока протекает одно и то же количество жидкости.
Ранее установлено, что  , т.е. поле ротора любого векторного поля трубчатое. Поэтому каждое трубчатое поле является полем ротора некоторого векторного поля. Если
, т.е. поле ротора любого векторного поля трубчатое. Поэтому каждое трубчатое поле является полем ротора некоторого векторного поля. Если 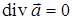 , то существует такое поле
, то существует такое поле  , что
, что  . Примером соленоидального поля является магнитное поле, т.к.
. Примером соленоидального поля является магнитное поле, т.к. 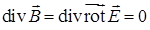 , что подтверждает отсутствие магнитных зарядов.
, что подтверждает отсутствие магнитных зарядов.
Определение. Потенциальное (безвихревое) поле – это векторное поле  , во всех точках которого ротор равен нулю:
, во всех точках которого ротор равен нулю:
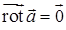 .
.
Это равносильно условию
 ,
,  ,
,  ,
,
oткуда  – полный дифференциал функции u(x,y,z), причем
– полный дифференциал функции u(x,y,z), причем
 ,
,  ,
, 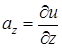 .
.
Это значит, что вектор  потенциального поля является градиентом скалярного поля:
потенциального поля является градиентом скалярного поля:
 .
.
Функция 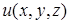 называется потенциалом векторного поля.
называется потенциалом векторного поля.
В потенциальном поле циркуляция по любому замкнутому контуру в силу формулы Стокса равна нулю. С точки зрения течения жидкости равенство нулю циркуляции означает, что в потоке нет замкнутых струек жидкости, т.е. нет водоворотов.
Работа в силовом потенциальном поле равна разности потенциалов в конечной и начальной точках линии L:
 .
.
Определение. Гармоническое поле – это векторное поле  , одновременно являющееся и потенциальным, и трубчатым.
, одновременно являющееся и потенциальным, и трубчатым.
Поскольку поле потенциально, его можно записать
 ,
,
где u – потенциал поля.
Условие трубчатости означает
 или
или
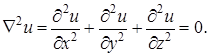
Функция u, подчиняющаяся этому условию, называется гармонической.
 2020-06-29
2020-06-29 479
479






