Задание.
- Переписать текст задачи, заменяя все параметры их значениями для решаемого варианта.
- Определить исходные данные и результаты.
- Установить, какие формулы следует использовать для вычислений и выполнить вычисления при помощи микрокалькулятора и таблиц.
- Построить требуемые графики.
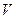 - порядковый номер в групповом журнале.
- порядковый номер в групповом журнале.
Задача 1. В каждом из 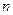 независимых испытаний событие
независимых испытаний событие 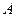 происходит с постоянной вероятностью
происходит с постоянной вероятностью 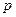 . Найти вероятность того, что событие
. Найти вероятность того, что событие 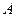 происходит:
происходит:
а) точно 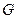 раз;
раз;
б) точно 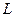 раз;
раз;
в) меньше чем 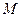 и больше чем
и больше чем 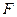 раз;
раз;
г) меньше чем 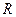 раз.
раз.
Значения параметров 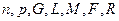 вычислить по следующим формулам:
вычислить по следующим формулам:
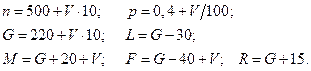
Задача 2. В каждом из 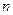 независимых испытаний событие
независимых испытаний событие 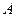 происходит с постоянной вероятностью
происходит с постоянной вероятностью 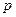 . Найти вероятность того, что событие
. Найти вероятность того, что событие 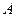 происходит:
происходит:
а) точно 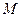 раз;
раз;
б) меньше чем 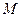 и больше чем
и больше чем 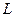 раз;
раз;
в) больше чем 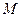 раз.
раз.
Значения параметров 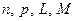 вычислить по следующим формулам:
вычислить по следующим формулам:
Задача 3. На телефонной станции неправильное соединение происходит с вероятностью 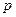 . Найти вероятность того, что среди
. Найти вероятность того, что среди 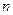 соединений имеет место:
соединений имеет место:
а) точно 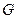 неправильных соединений;
неправильных соединений;
б) меньше чем 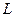 неправильных соединений;
неправильных соединений;
в) больше чем 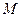 неправильных соединений.
неправильных соединений.
Значения параметров 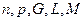 вычислить по следующим формулам:
вычислить по следующим формулам:
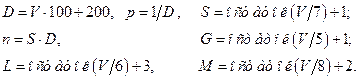
Задача 4. В каждом из 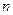 независимых испытаний событие
независимых испытаний событие 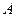 происходит с постоянной вероятностью
происходит с постоянной вероятностью 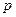 . Найти вероятность того, что относительная частота
. Найти вероятность того, что относительная частота 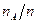 этого события отличается по абсолютной величине от вероятности
этого события отличается по абсолютной величине от вероятности 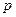 не больше чем на
не больше чем на 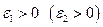 .
.
Значения параметров 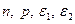 вычислить по следующим формулам:
вычислить по следующим формулам:
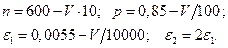
Задача 5. Случайная величина 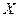 задана рядом распределения
задана рядом распределения
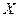
| 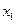
| 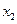
| 
| 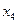
|
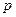
| 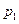
| 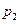
| 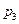
| 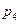
|
Построить полигон распределения. Найти функцию распределения 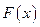 случайной величины
случайной величины 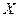 и построить ее график. Вычислить для
и построить ее график. Вычислить для 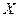 ее математическое ожидание, дисперсию и моду.
ее математическое ожидание, дисперсию и моду.
Значения параметров 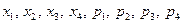 вычислить по следующим формулам:
вычислить по следующим формулам:
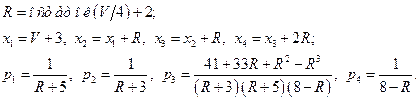
Задача 6. Случайная величина 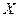 задана функцией плотности вероятности
задана функцией плотности вероятности 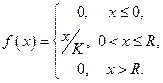
Найти функцию распределения 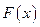 случайной величины
случайной величины 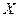 . Построить графики функций
. Построить графики функций 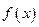 и
и 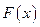 . Вычислить для
. Вычислить для 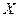 ее математическое ожидание, дисперсию, моду и медиану.
ее математическое ожидание, дисперсию, моду и медиану.
Значения параметров 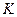 и
и 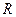 вычислить по следующим формулам:
вычислить по следующим формулам:
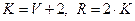 .
.
Задача 7. Случайная величина 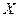 задана функцией распределения
задана функцией распределения 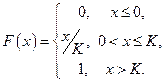 Найти функцию плотности вероятности
Найти функцию плотности вероятности 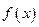 случайной величины
случайной величины 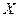 . Построить графики функций
. Построить графики функций 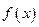 и
и 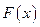 . Вычислить для
. Вычислить для 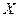 ее математическое ожидание, дисперсию, моду и медиану.
ее математическое ожидание, дисперсию, моду и медиану.
Значение параметра 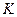 вычислить по формуле:
вычислить по формуле: 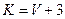 .
.
Задача 8. Задана случайная величина 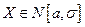 . Найти вероятность того, что эта случайная величина принимает значение:
. Найти вероятность того, что эта случайная величина принимает значение:
а) в интервале 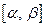 ;
;
б) меньше 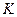 ;
;
в) больше 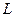 ;
;
г) отличающееся от своего среднего значения по абсолютной величине не больше чем на 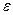 .
.
Значения параметров 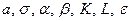 вычислить по следующим формулам:
вычислить по следующим формулам:
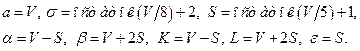
Задача 9. Задана случайная величина 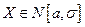 и точки
и точки 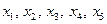 на числовой оси, разделяющие ее на шесть интервалов. Найти вероятность того, что Случайная величина
на числовой оси, разделяющие ее на шесть интервалов. Найти вероятность того, что Случайная величина 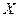 принимает значения в этих интервалах.
принимает значения в этих интервалах.
Значения параметров 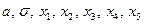 вычислить по следующим формулам:
вычислить по следующим формулам:
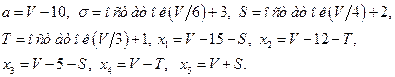
 2020-06-30
2020-06-30 114
114






